LLM高效预训练(二)

发表于 2024-09-29 更新于 2024-10-01 分类于 CS ， NLP ， LLM 本文字数： 13k 阅读时长 ≈ 23 分钟

【本文已在同名微信公众号 / 知乎 / 个人博客linsight.cn 上线】

从目前的实践结果来看，从大模型通过裁剪、蒸馏等手段获取小模型，效果是比较好的，同时成本也相比直接从零预训练要低廉得多，而且也免去了大量收集数据和清洗数据的工作。

今天就集中讲一下模型裁剪的工作。

裁剪 + 蒸馏

论文：《Compact Language Models via Pruning and Knowledge Distillation》 & 《LLM Pruning and Distillation in Practice: The Minitron Approach》

时间：2024年7月 & 2024年8月

机构：NVIDIA

这两篇实际上是一个内容，后一篇是前一篇的整合和完整版，增加了基于Llama-3.1和Mistral的实验。《Compact》更像是比较混杂的实验报告。

英伟达提出的方法简单来说就是通过对已有的大模型进行裁剪，并对裁剪后的小模型使用蒸馏训练进行效果恢复（效果恢复的训练称之为retrian）。这么做可以以<3%的retrain训练量，获得比从零训练的小模型更好的效果。

Nemotron-4 15B裁剪到MINITRON 8B和4B的效果如下：

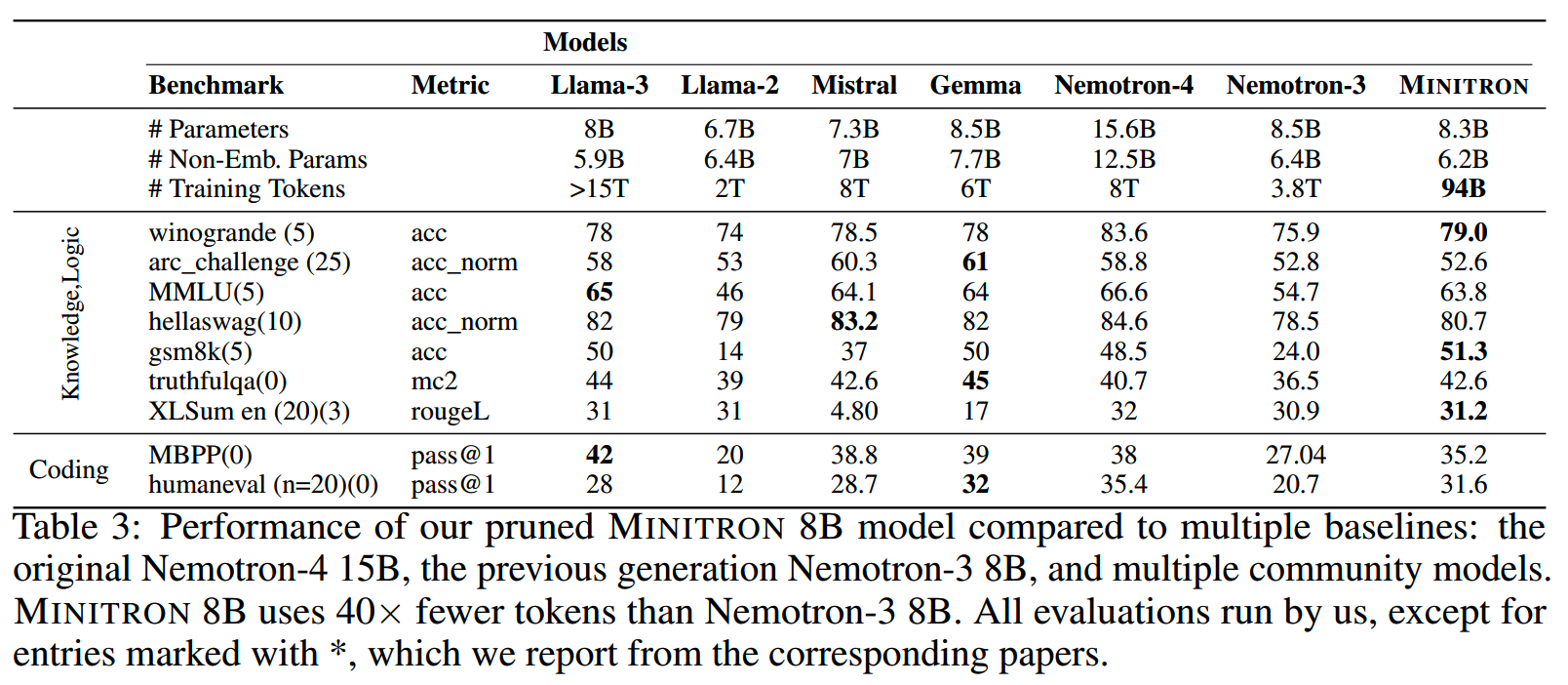
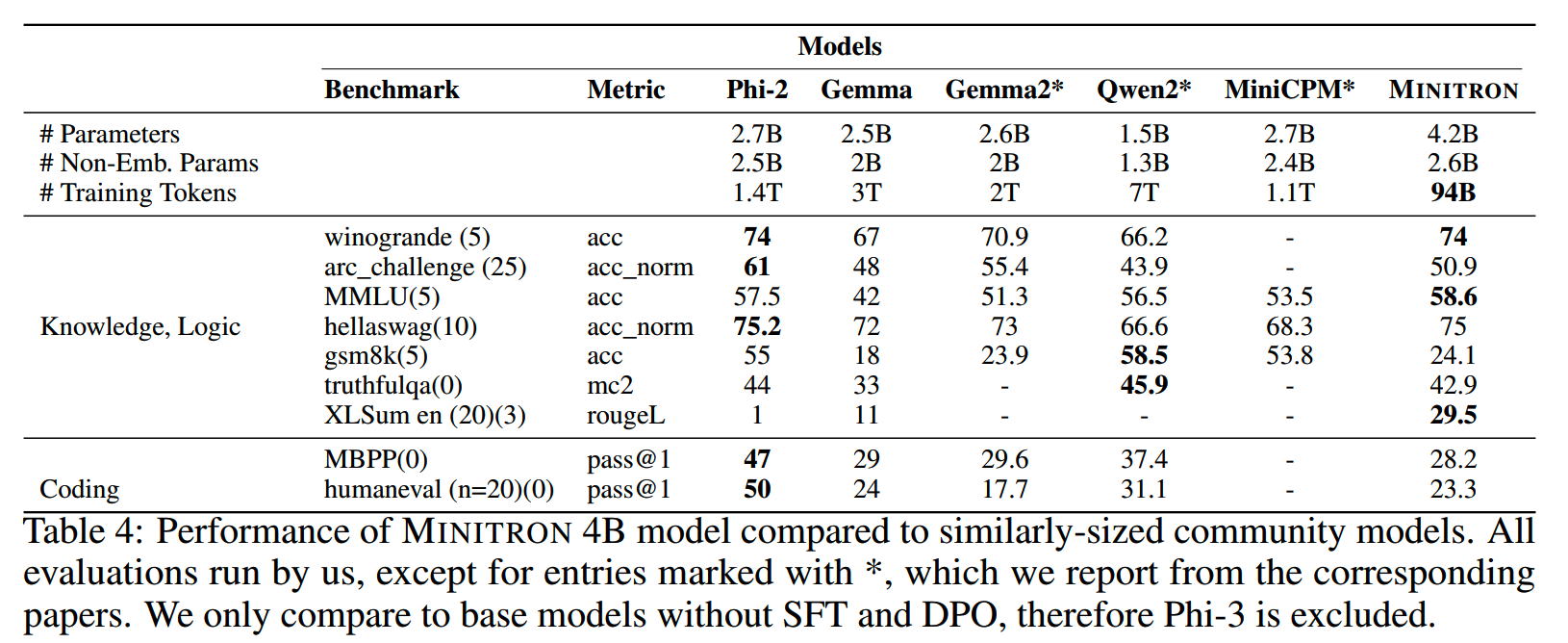
整体的方案示意图如下：

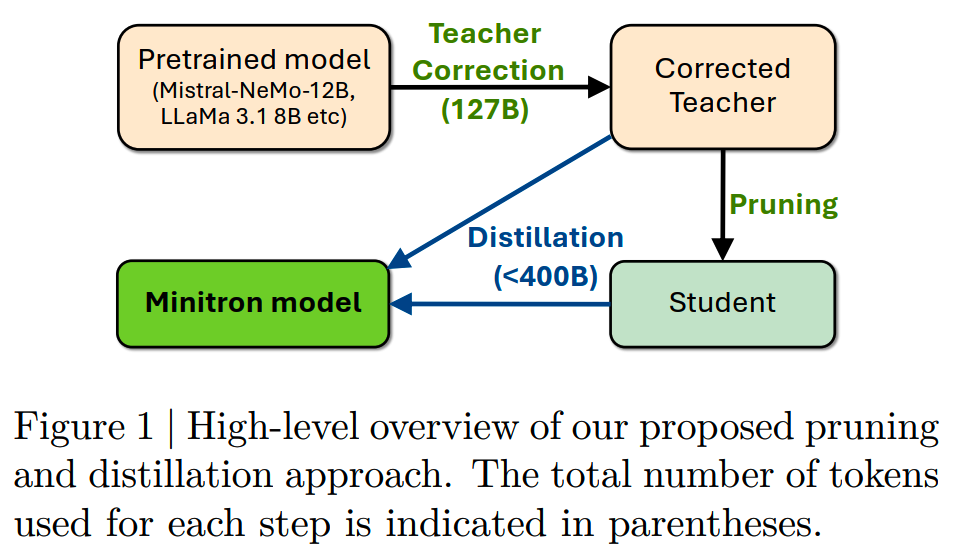
接下来看下每个步骤具体怎么做。

Teacher Correction

很多情况下我们会使用开源的模型作为裁剪的teacher模型，因为选择比较多，效果更好。但是如果使用开源模型会有一个问题，那就是我们没有开源模型的训练数据。这样在后面使用自己的数据进行蒸馏的步骤中，就有可能出现因为数据分布的偏移，影响了teacher模型的效果，导致蒸馏训练效果不好的情况。

那么缓解这个问题的一个方法，就是在裁剪和蒸馏之前先用部分自有的训练数据对teacher模型进行微调。这个过程就叫teacher correction。

下图对比了使用和不使用teacher correction的情况下，把Mistral NeMo 12B裁剪到8B后，8B模型的训练loss下降情况：

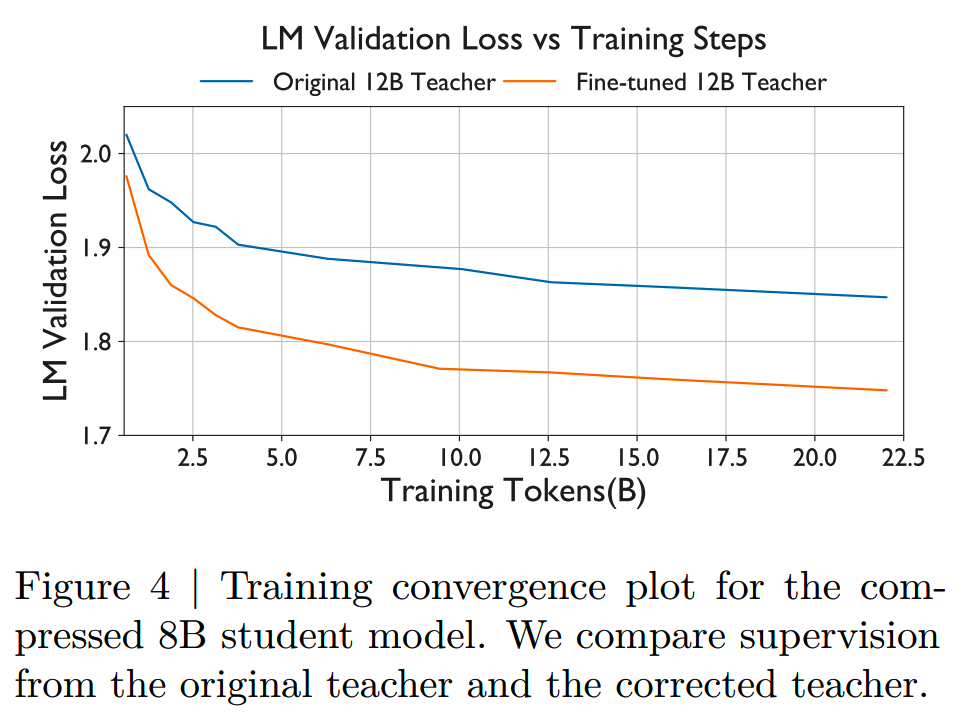
在对12B模型使用了teacher correction的情况下，8B模型的loss保持相对较低。

实验中，teacher correction阶段使用了~127B的token。

参数裁剪

和我们在上一篇讲到的weight subcloning类似，NVIDIA也通过计算neuron的重要性来决定裁剪/保留哪些参数。而NVIDIA仅使用了1024个sample作为裁剪的calibration dataset，用于获得各个参数的activation。

参数裁剪分为深度裁剪和宽度裁剪。

1、宽度裁剪

宽度的裁剪包括几个部分：neuron裁剪、attention head裁剪和embedding裁剪。这几个部分的重要性计算方法如下：

注意力部分的裁剪以头为单位，计算每个头输出的L2 norm：

\[F_{\mathrm{head}}^{(i)}=\sum_{\mathrm{B,S}}\|\operatorname{Attn}(\mathbf{X}\boldsymbol{W}^{Q,i},\mathbf{X}\boldsymbol{W}^{K,i},\mathbf{X}\boldsymbol{W}^{V,i})\|_2\]

对于MLP层，有 $\mathrm{MLP}(\mathbf{X})=\delta\left(\mathbf{X}\cdot W_1^T\right)\cdot W_2$，以投影后的输出值作为neuron的重要性：

\[F_{\mathrm{neuron}}^{(i)}=\sum_{\mathrm{B,s}}\mathrm{X}(W_1^i)^T\]

而embedding层则是以LN后的值作为重要性衡量：

\[F_{\mathrm{emb}}^{(i)}=\sum_{\mathrm{B,S}}LN(\mathrm{X})_i\]

注意这里在batch和sequence维度上都是直接求和。实际上论文中验证了三种不同的方法：mean、L2 norm和variance。在batch和sequence维度上分别使用这三种不同的aggregation方法，效果对比如下：

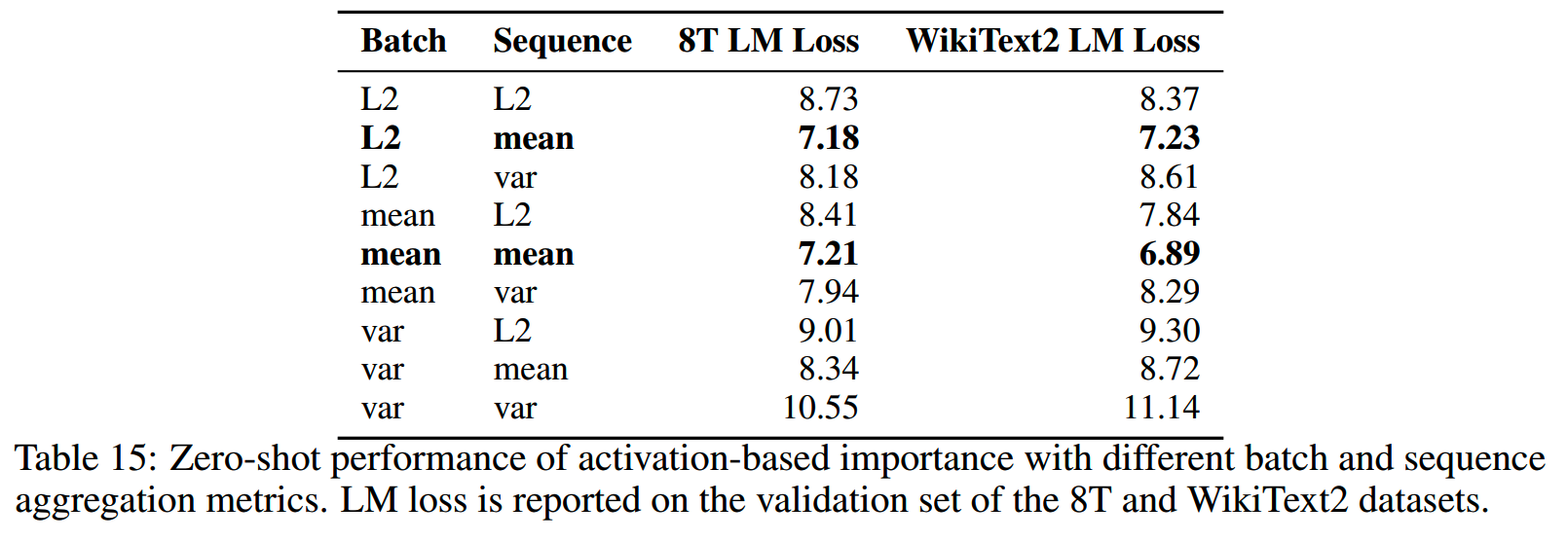
使用（L2，mean）和（mean，mean）的效果最好。

NVIDIA这里在宽度裁剪的时候，并没有特别关注使用残差连接的层，而是直接把它们当成独立的参数进行裁剪，这里稍微有点奇怪。

2、深度裁剪

论文使用了2种模型深度裁剪的方法：
- PPL：通过移除一层或多层的模型，对比移除前后同样输入的PPL变化，就可以得出被移除的层对模型输出的影响程度，这个影响程度就可以作为这一层或者多层的重要度衡量
- Block Importance（BI）：对某一层或连续多层的输入输出按如下cosine distance计算获得层重要度：

\[\mathrm{BI}_i=1-\mathbb{E}_{X,t}\frac{\mathrm{X}_{i,t}^T\mathrm{X}_{i+1,t}}{\|\mathrm{X}_{i,t}\|_2\|\mathrm{X}_{i+1,t}\|_2}\]

BI的计算用的就是ShortGPT的方法。

3、获取student模型

获得各个维度的重要度之后，就要决定各个维度分别保留多少参数。

一般来说，我们会有一个target size，以及一系列的常用模型结构配置。可以把这些配置组合起来，保留那些总参数量符合我们要求的：

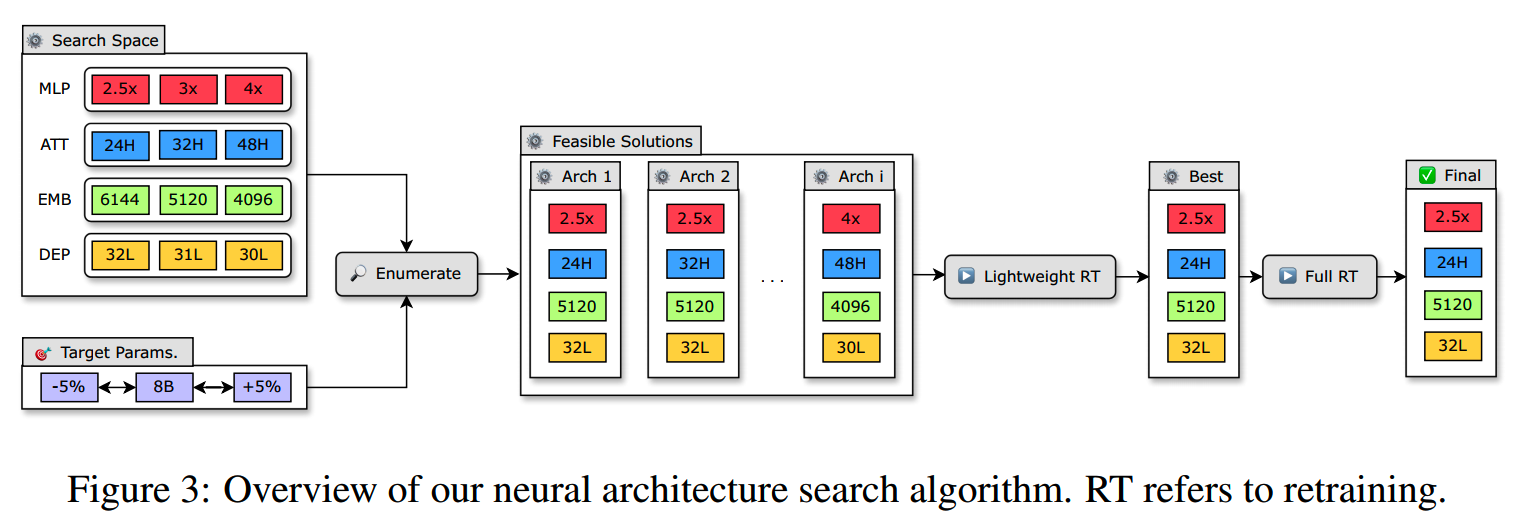
按上图这些组合，最终有十几二十个符合总参数量要求的configuration，还算在可以接受的范围内。

然后对比所有裁剪出来的candidate的效果，保留效果最好的。由于裁剪会让模型的输出变差很多，所以并不直接对比裁剪后的candidate，而是会进行轻量级的训练。论文中是使用了~1.8B的参数对各个候选模型进行了训练：

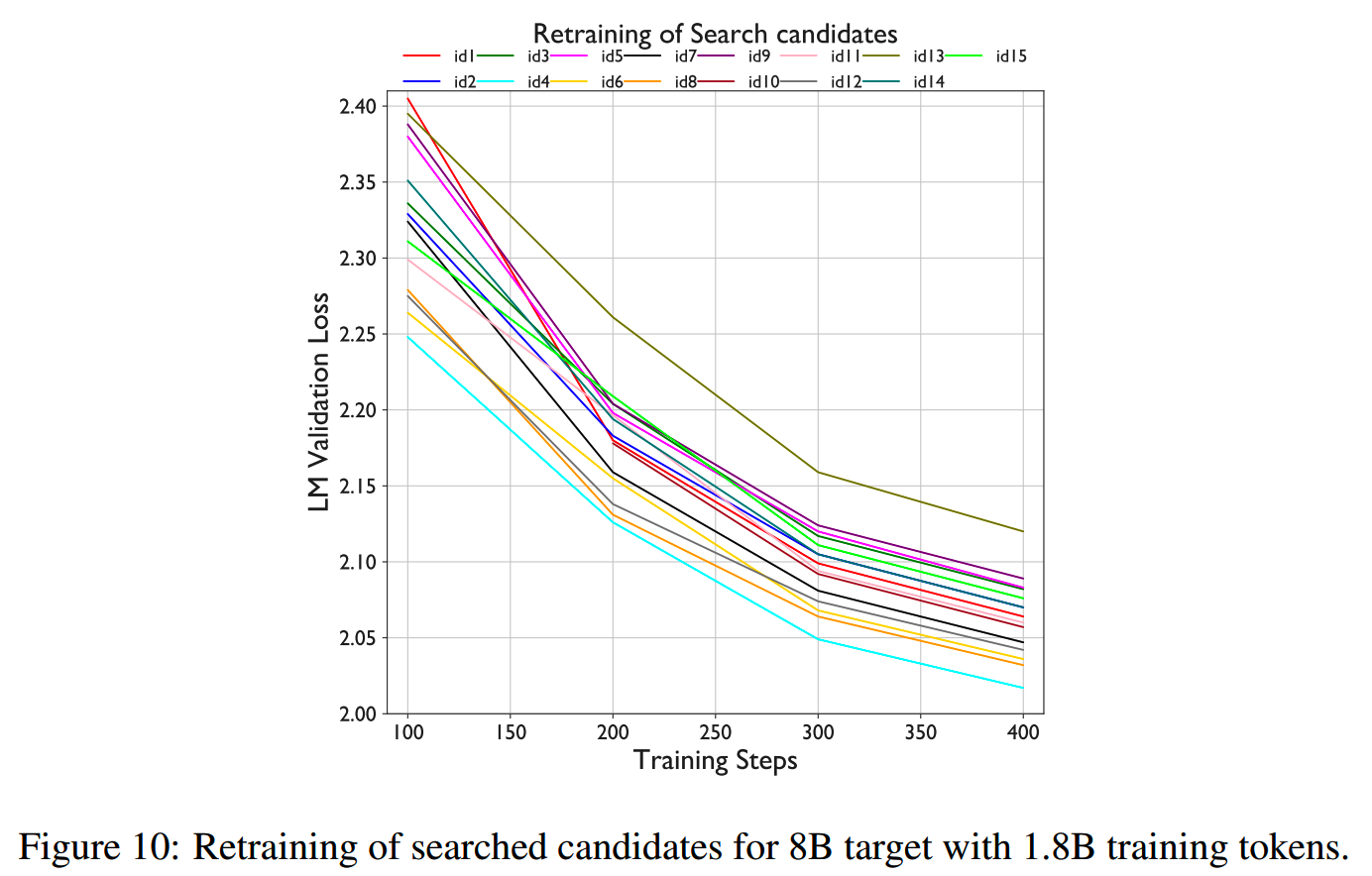
轻量级的训练结果表明只需几百步的训练就能得到这些candidate效果的rank，并且比较稳定。

retrain

retrain阶段以蒸馏的方式进行训练，实验中总的训练量只有不到100B。

对于一个LM，一个token xi的输出分布是：

\[p(x_i,\tau)=\frac{\exp\left(\frac{x_i}\tau\right)}{\sum_{j=1}^{|V|}\exp\left(\frac{x_j}\tau\right)}\]

其中 $\tau$ 是温度。那么整个sequence的logit-based KD loss就是：

\[L_{\mathrm{logits}}=\frac1l\sum_{k=1}^l\mathrm{Loss}(p_t^k(x,\tau),p_s^k(x,\tau))\]

这是经典的蒸馏loss。也可以增加intermediate state-based KD loss，也就是用中间层的hidden state计算loss：

\[L_{is}=\frac1l\sum_{k\in H}\sum_{i=1}^lLoss_k(h_t^{ki},h_s^{ki})\]

那么最终的训练损失是：

\[L=L_{\mathbf{CLM}}+L_{logits}+\alpha\times L_{is}\]

实验

论文中给出的一些实践经验，挑了一些有用的放这。

1、iterative or not？

对于给定的student model的总参数量，我们有各种不同大小的模型可以作为teacher model。那么一个自然的想法就是，如果teacher模型和studnet模型的参数规模差得很多，那增加一些中间量级的操作（iteration）是不是效果能更好？比如teacher模型的大小是15B，目标的student模型大小为4B，那我先把15B裁剪成8B，训练好之后再把8B裁剪成4B效果会不会比直接把15B裁剪成4B更好？

答案是no。下图是实验的数据，T是iteration的次数，T=1是直接一步到位，T=2则是增加1个中间量级。

虽然iteration的操作使得目标student模型裁剪后的初始loss较小，但是经过训练之后所有模型都收敛到相同的水平，因此没有必要浪费算力去做中间规模的模型，直接一步到位就行了。

2、宽度裁剪和深度裁剪的对比

用Nemotron-15B裁剪成8B，不同维度的裁剪结果如下：

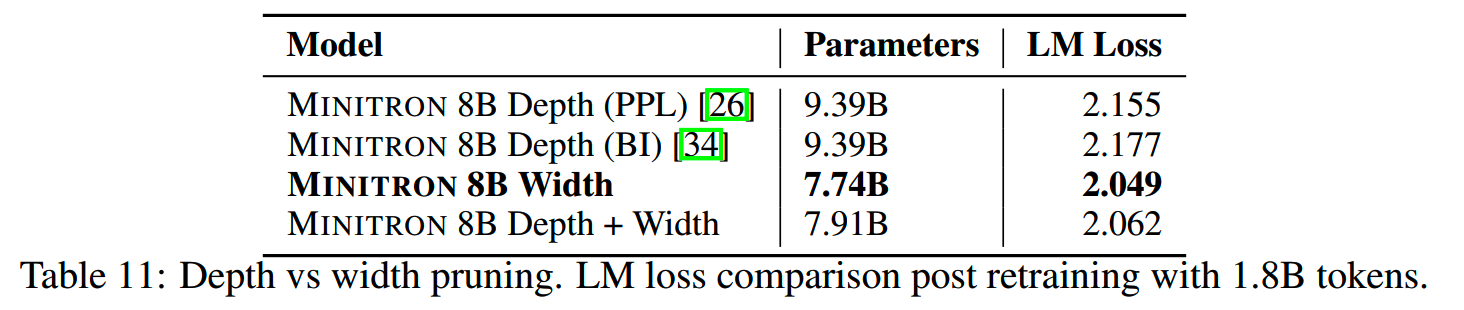
结果上看，宽度裁剪的损失更少。这和我们已有的认知是符合的：相同参数的情况下，更深的模型一般会有更好的效果。深度裁剪保留了teacher模型的深度，使得student模型的实际容量更大。

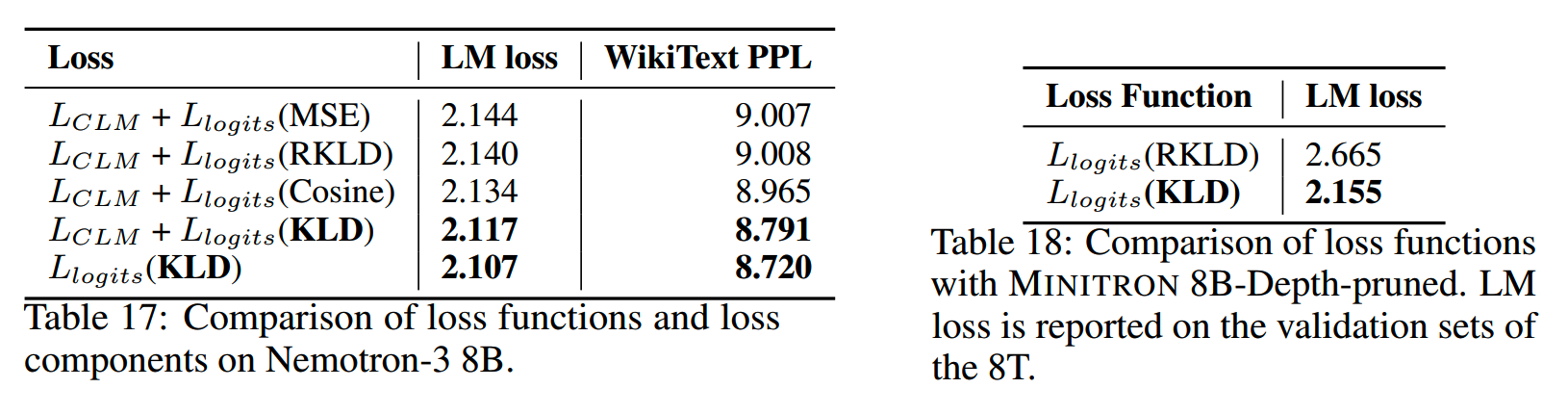
3、蒸馏损失

前面提到使用KLD作为蒸馏损失，实际上还有很多其他变体可以选择：MSE、cosine similarity、reverse KLD等。最终还是KLD最好：

4、Single vs Multi-Phase Retraining

这一点还是蛮重要的。现在的预训练模型基本都是包含两阶段的做法：
- phase1：大量的通用数据
- phase2：相比phase1量级较少，但是质量更高，和下游任务更紧密的数据

那么用哪个阶段的模型裁剪更好的呢？方案（1）是用phase1的teacher checkpoint进行裁剪，然后对student进行phase1和phase2的训练；方案（2）是用teacher模型的phase2 checkpoint进行裁剪，然后对student模型进行phase2数据的训练。

两种方案的对比如下：

结果上看，第二种方案，也就是仅使用phase2的checkpoint和数据，效果更好。

成本的节约

假设我们原来的方案是从零训练Nemotron-4的15B、8B和4B三个规模的模型，三个模型每一个step的训练计算量分别是4.4e17, 2.5e17 and 1.2e17，那么总的训练量就是(4.4e17+2.5e17+1.2e17)×steps。

现在我们先训练了15B模型，然后从15B模型裁剪+蒸馏得到8B和4B模型，而蒸馏所需的数据很少，总的计算量只有从0训练的1/40，那么总的计算量为 (4.4e17 + 2.5e17/40 + 1.2e17/40) × steps。

结论是通过裁剪+蒸馏的方案，可以节省接近一半的总计算量，而两个小规模模型的效果甚至更好。

基于L0剪枝

论文：《Learning Sparse Neural Networks through L0 Regularization》

时间：2017年12月

TL;DR

提出hard concrete distribution，把基于L0 norm的参数裁剪变得可以直接训练学习。

方法

模型一般都是过参数化的（overparametrized），所以可以在裁剪掉部分参数的情况下，保持效果基本不变。

L0 regularization会对所有非0参数施加固定的惩罚：

\[\mathcal{R}(\boldsymbol{\theta})=\frac1N\bigg(\sum_{i=1}^N\mathcal{L}\big(h(\mathbf{x}_i;\boldsymbol{\theta}),\mathbf{y}_i\big)\bigg)+\lambda\|\boldsymbol{\theta}\|_0\]

\[\|\theta\|_0=\sum_{j=1}^{|\theta|}\mathbb{I}[\theta_j\neq0]\]

h是模型，L(·)是原模型的loss function，N是数据集的size。

通过最小化

\[\boldsymbol{\theta}^*=\arg\min_{\boldsymbol{\theta}}\{\mathcal{R}(\boldsymbol{\theta})\}\]

我们就能得到最佳的稀疏参数组合。

但是这里需要遍历所有可能的参数组合，也就是说最多需要验证 $2^{|\theta|}$ 次损失。这对于参数量巨大的模型显然是不可行的。

需要手动遍历所有可能是因为上面的这个计算是离散的，因此需要想办法把这个loss变得平滑可导。

考虑 $\theta$ 重参数化下的L0 norm：

\[\theta_j=\tilde{\theta}_jz_j,\quad z_j\in\{0,1\},\quad\tilde{\theta}_j\neq0,\quad\|\boldsymbol{\theta}\|_0=\sum_{j=1}^{|\theta|}z_j\]

z就是一个控制是否保留对应参数的binary gate，而L0 norm则表示打开的gate的数量。

既然z是二值的（0/1），我们可以让z来自伯努利分布：

\[q(z_{j}|\pi_{j})=\mathrm{Bern}(\pi_{j})\]

基于此，可以把R改写一下：

\[\mathcal{R}(\tilde{\boldsymbol{\theta}},\boldsymbol{\pi})=\mathbb{E}_{q(\mathbf{z}|\boldsymbol{\pi})}\left[\frac1N\left(\sum_{i=1}^N\mathcal{L}\left(h(\mathbf{x}_i;\tilde{\boldsymbol{\theta}}\odot\mathbf{z}),\mathbf{y}_i\right)\right)\right]+\lambda\sum_{j=1}^{|\theta|}\pi_j\]

\[\tilde{\boldsymbol{\theta}}^*,\boldsymbol{\pi}^*=\arg\min\{\mathcal{R}(\tilde{\boldsymbol{\theta}},\boldsymbol{\pi})\}\]

$$ 是elementwise product。

这里第二项是连续可导的了，但是第一项里的离散z依然让第一项难以用梯度训练。

那就需要把z给变成连续的。

考虑一个来自分布q的s：

\[\mathrm{s}\sim q(\mathrm{s}|\phi)\]

用hard-sigmoid把它转成0~1的值

\[\mathbf{z=min(1,max(0,s))}\]

那么就有

\[q(\mathbf{z}\neq0|\phi)=1-Q(\mathbf{s}\leq0|\phi)\]

Q是cumulative distribution function (CDF)。

基于这个分布，可以进一步把上面的R进行平滑：

\[\mathcal{R}(\tilde{\boldsymbol{\theta}},\phi)=\mathbb{E}_{q(\mathbf{s}|\boldsymbol{\phi})}\left[\frac1N\left(\sum_{i=1}^N\mathcal{L}\big(h(\mathbf{x}_i;\tilde{\boldsymbol{\theta}}\odot g(\mathbf{s})),\mathbf{y}_i\big)\right)\right]+\lambda\sum_{j=1}^{|\theta|}\left(1-Q(s_j\leq0|\phi_j)\right)\]

\[\tilde{\boldsymbol{\theta}}^*,\phi*=\arg\min_{\tilde{\boldsymbol{\theta}},\boldsymbol{\phi}}\{\mathcal{R}(\tilde{\boldsymbol{\theta}},\phi)\},\quad g(\cdot)=\min(1,\max(0,\cdot))\]

那么s具体一个用什么分布呢？

论文提出了hard concrete distribution。简单来说是这样一个分布：

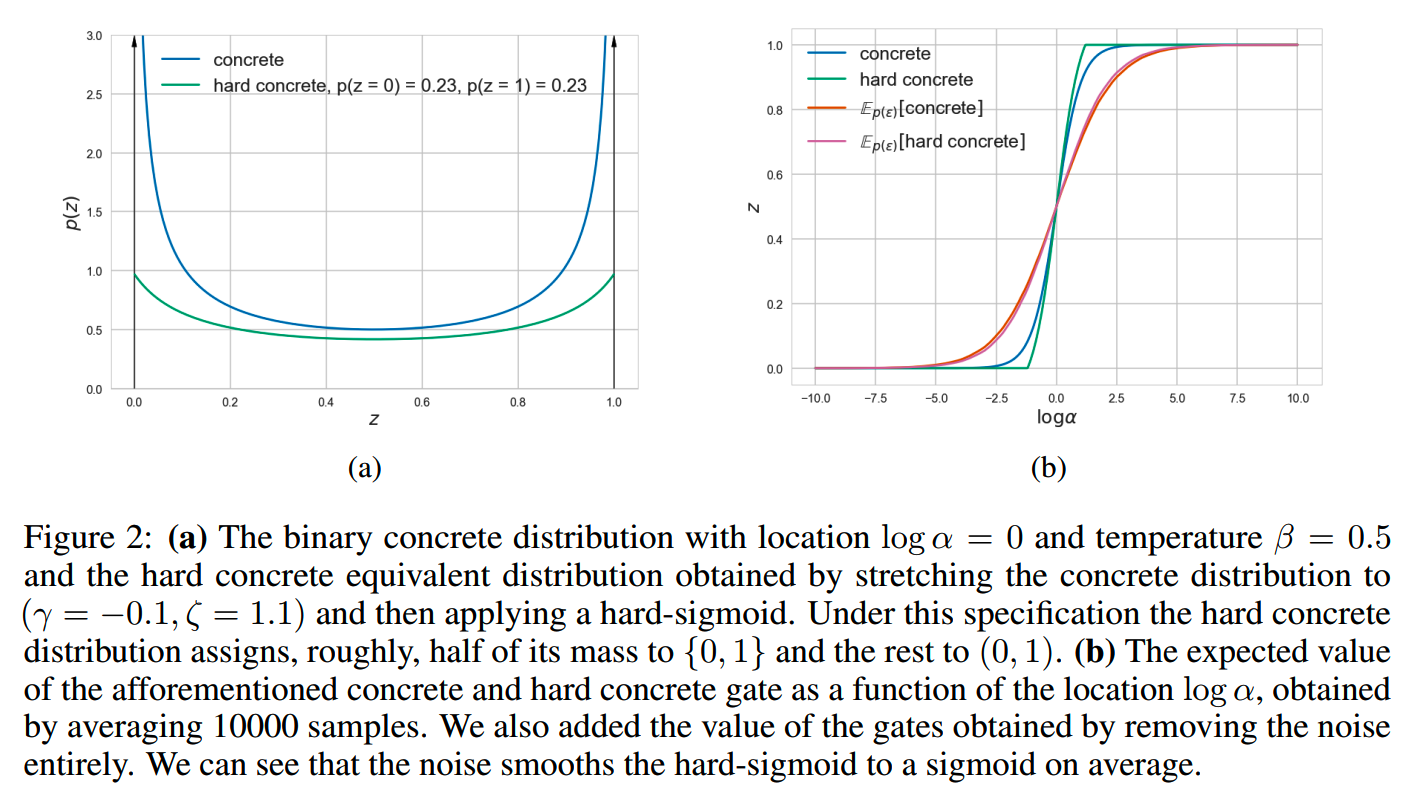
大部分的概率集中在靠近0和靠近1的两端，能够在保持平滑的同时，指出每个参数是否要保留。

Shortened LLaMA

论文：《Shortened LLaMA: Depth Pruning for Large Language Models with Comparison of Retraining Methods》

时间：2024年2月

Shortened LLaMA的做法是仅对模型层数进行裁剪。为什么要仅对深度进行裁剪呢，论文的说法是可以提升裁剪后模型的推理速度，减少推理显存的需求。下面看看论文的一些细节，摘取一些可以参考的地方。

层重要性

裁剪模型核心问题就是找到那些参数更重要。既然是对层进行裁剪，那么要做的就是计算整个transformer block的重要性。

对于一个linear weight matrix，其参数是一个size为 $(d_\mathrm{out},d_\mathrm{in})$ 的矩阵：

\[\mathrm{W}^{k,n}=\begin{bmatrix}W_{i,j}^{k,n}\end{bmatrix}\]

n是层index，k是这个矩阵的operation type，比如是query的投影矩阵，或者是MLP层的up matrix。

文中提出了几种计算方法。

1、Magnitude (Mag)

参考《Pruning filters for efficient convnets》中提出的计算方式，“weights with smaller norms are less informative”，因此直接对所有参数的绝对值求和：

\[I_{\mathrm{Magnitude}}^{n}=\sum_{k}\sum_{i}\sum_{j}\left|W_{i,j}^{k,n}\right|\]

2、Taylor

移除一个transformer block之后，如果模型的输出误差增大，那么说明这个层有影响。误差增大越多，层的重要性越大。

按泰勒展开，在忽略二阶导的情况下，这个误差可以表达为

\[\left|\mathcal{L}(W_{i,j}^{k,n};D)-\mathcal{L}(W_{i,j}^{k,n}=0;D)\right|\approx \left|\frac{\partial\mathcal{L}(D)}{\partial W_{i,j}^{k,n}}W_{i,j}^{k,n}\right|\]

L是training loss。因此整个层的重要性就是

\[I_{\mathrm{Taylor}}^n=\sum_k\sum_i\sum_j\left|\frac{\partial\mathcal{L}(D)}{\partial W_{i,j}^{k,n}}W_{i,j}^{k,n}\right|\]

3、Mag+ and Taylor+

用Mag或者Taylor计算层重要性的时候，会把early blocks判定为不重要。但是我们现在知道其实前几层和后基层对模型的整体结果影响都很大（《The state of sparsity in deep neural networks》、《Layer-adaptive sparsity for the magnitude-based pruning》），因此需要结合这个经验，把前4层和后2层保留下来，不纳入裁剪候选层中。这个也和《Llm-pruner: On the structural pruning of large language models》的做法一致。

4、PPL

除了可以使用training loss，也可以通过计算PPL看移除一个层之后的影响。

以上各种方法的实验效果对比如下：

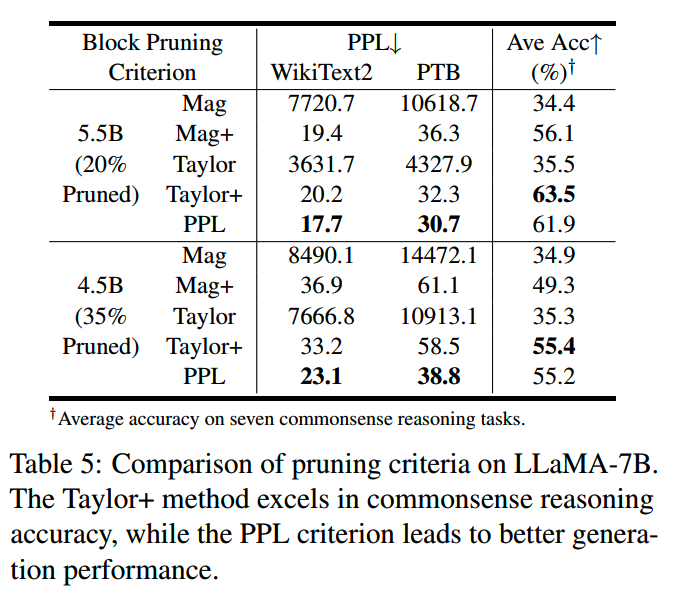
Taylor+ 和 PPL 的效果相对较好。

训练

1、one-shot or iteration

对于裁剪应该是一步到位，还是一步一步迭代进行，文中给出的答案是one-shot就足够了。一方面，多次迭代会引入更多的成本，另一方面，多次迭代对结果的影响并不显著，相比之下，retrain阶段才是对结果影响更大的一步。

2、更细粒度的裁剪

前面的裁剪是以整个transformer block为单位进行的，那么如果把粒度变小，对attention层和MLP层分开裁剪效果怎么样呢？结果是，还是以transformer block整体进行裁剪效果更好：

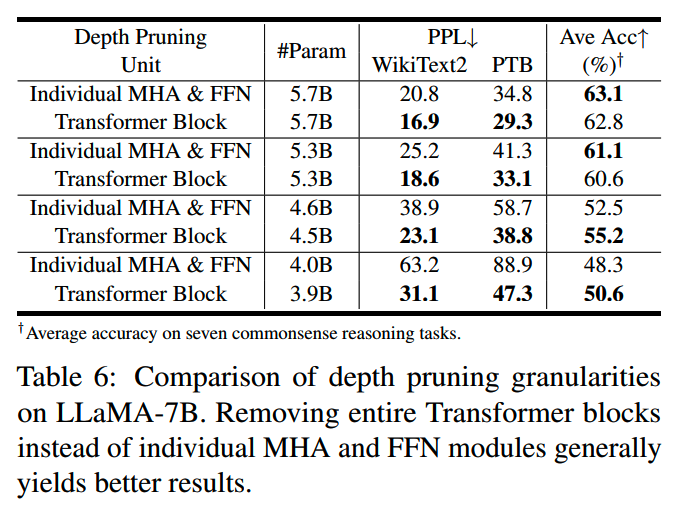
3、效果

分别对LLaMA-7B和Vicuna-13B-v1.3进行不同程度的裁剪和训练，效果如下：

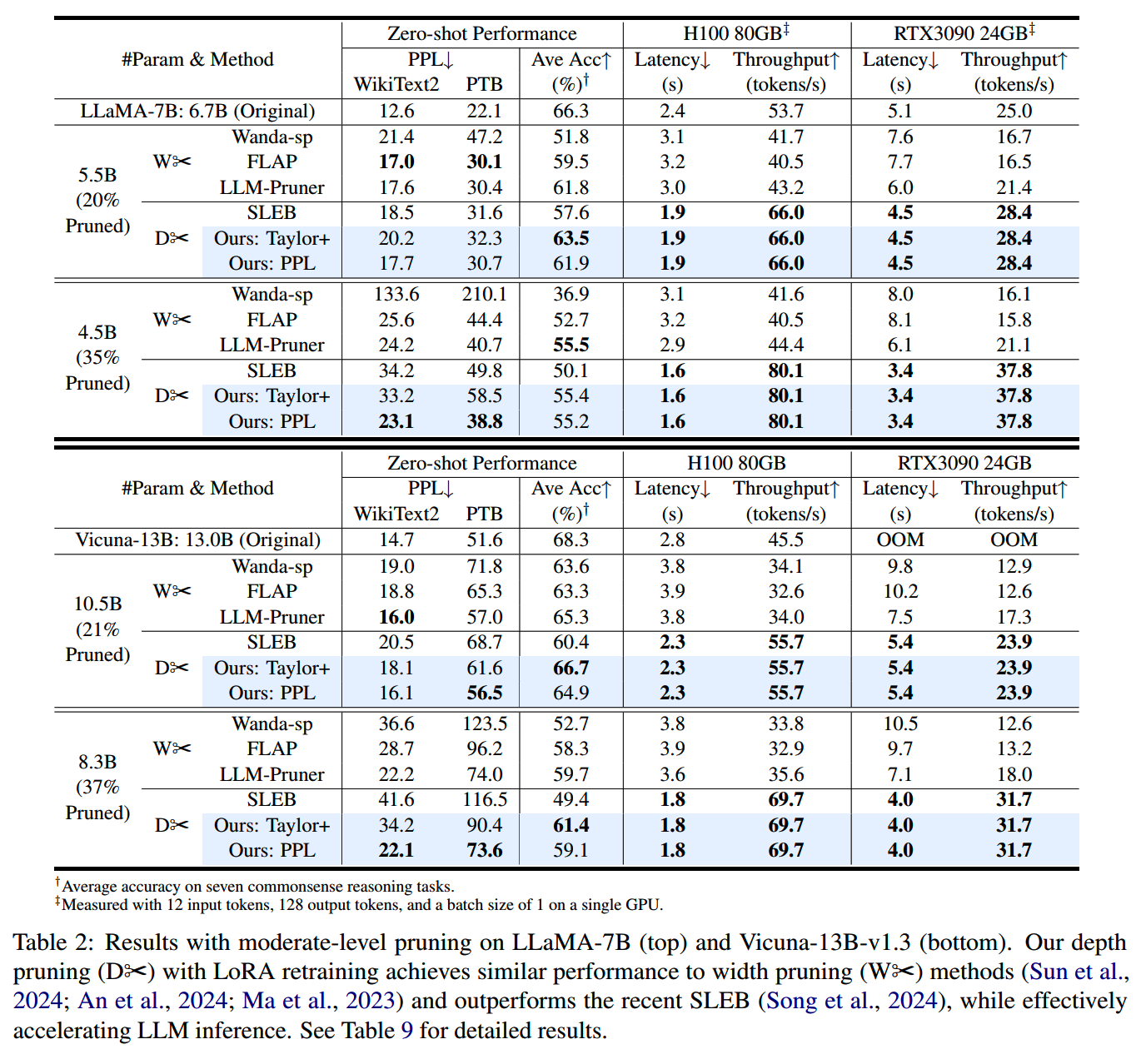
LaCo

论文：《Laco: Large language model pruning via layer collapse》

时间：2024年2月

LaCo = Layer Collapse

LaCo也是对模型的层数进行裁剪，不过被裁剪掉的层并不是直接抛弃，而是会通过参数合并的方式，尽量把效果保留下来。

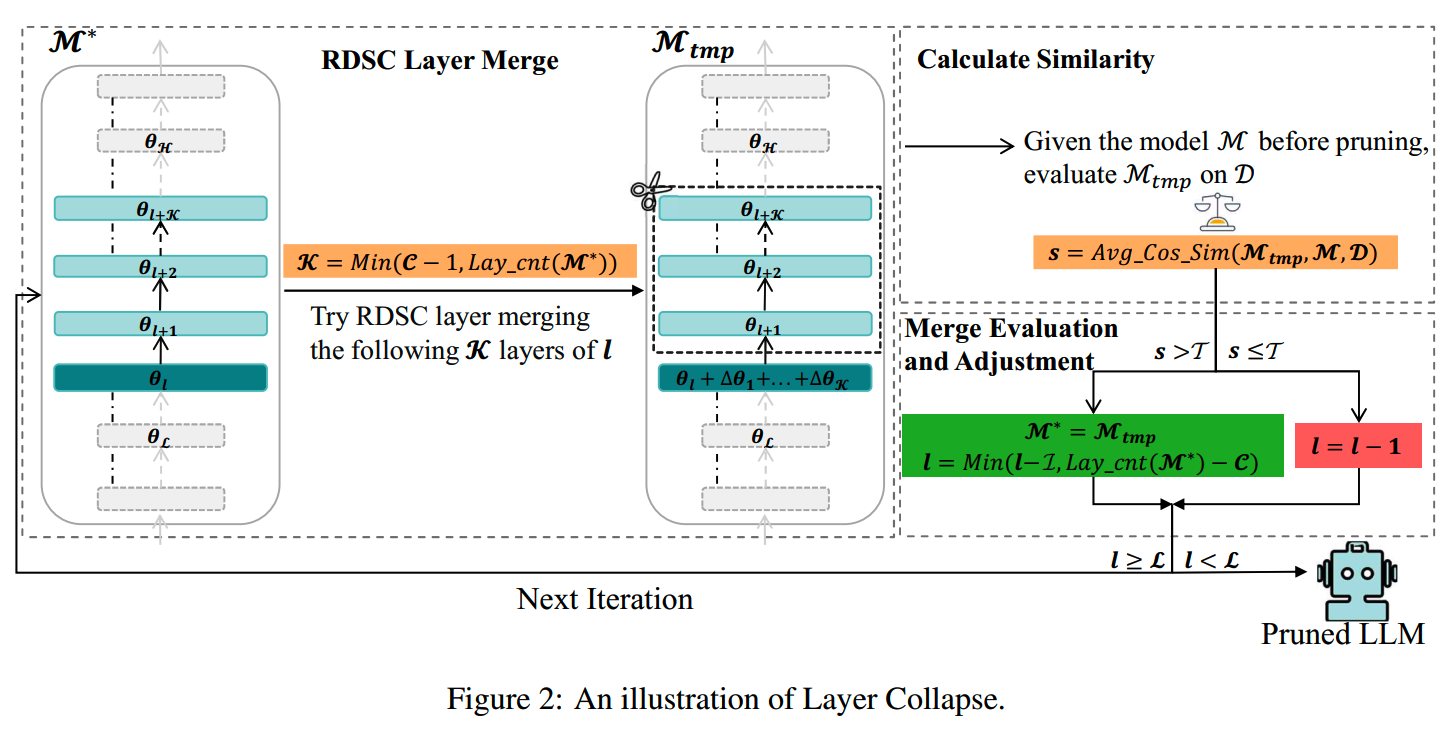
RDSC Layer Merge

RDSC = Reserving-Differences-while-Seeking-Common

对于模型中的某一层参数 $\theta_{l}$，以及跟在其后面的m层的参数，可以通过下面的方式把它们合并起来：

\[\begin{aligned}\theta_{l}^{*}&=\theta_l+(\theta_{l+1}-\theta_l)+\cdots+(\theta_{i+m}-\theta_l)\\&=\theta_l+\sum_{k=1}^m(\theta_{l+k}-\theta_l)\end{aligned}\]

模型层数裁剪

裁剪的算法如下：

解释一下：

（1-6行）首先，在准备阶段，需要定义几个参数：①每次合并操作要合并的层数C；②合并操作的层范围[L,H]；③相邻合并层之间的最小间隔I；④模型输出相似性阈值T；此外还要准备calibration数据集D。
（10-11行）RDSC Layer Merge：每次迭代，尝试将层l后面的K层合并到层l中，获得临时模型M_tmp。
（12行）Calculate Similarity：前向计算获得M_tmp和原始模型M在D上的句子表示，并计算两个表示之间的cosine similarity，得到平均相似度s。
（13-21行）Merge Evaluation and Adjustment：如果s>T，则合并成功，将M_tmp用于下一次迭代，否则l=l-1，进入下一次迭代。

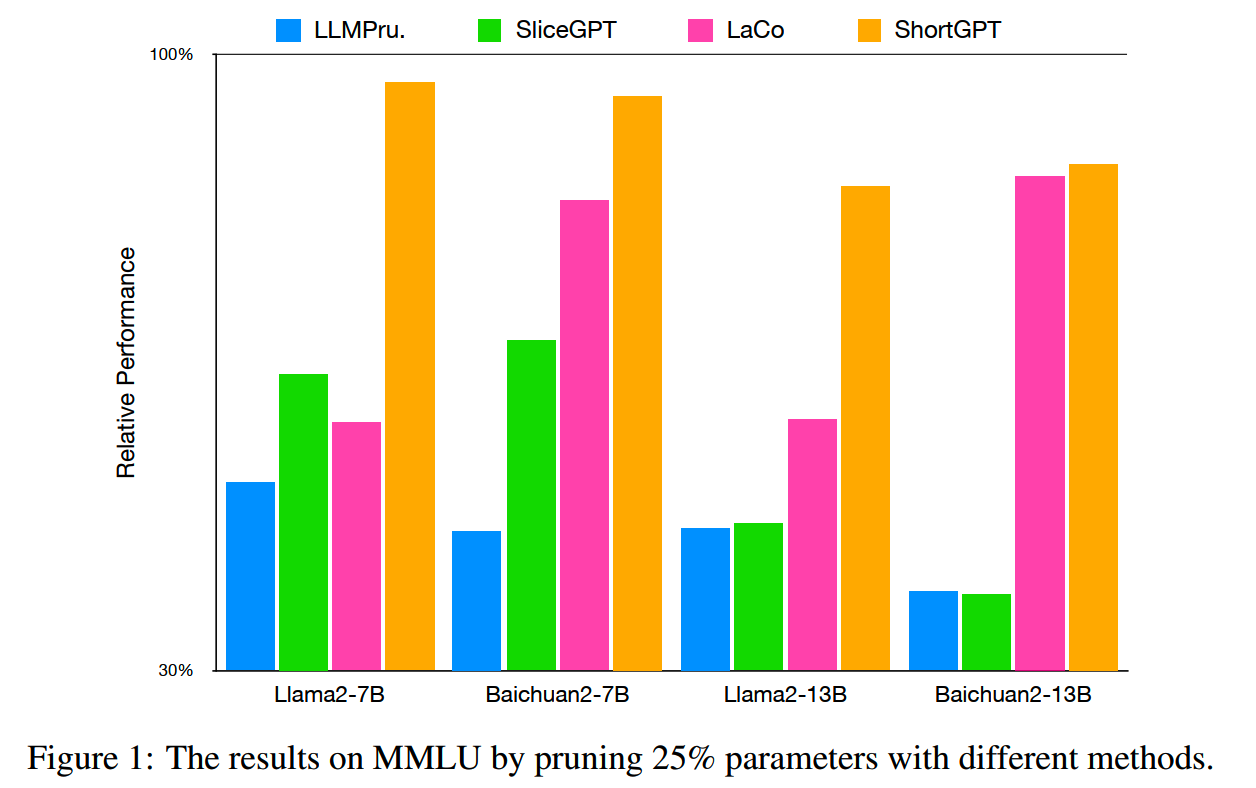
ShortGPT

论文：《ShortGPT: Layers in Large Language Models are More Redundant Than You Expect》

时间：2024年3月

ShortGPT也是仅对模型层数进行的裁剪。

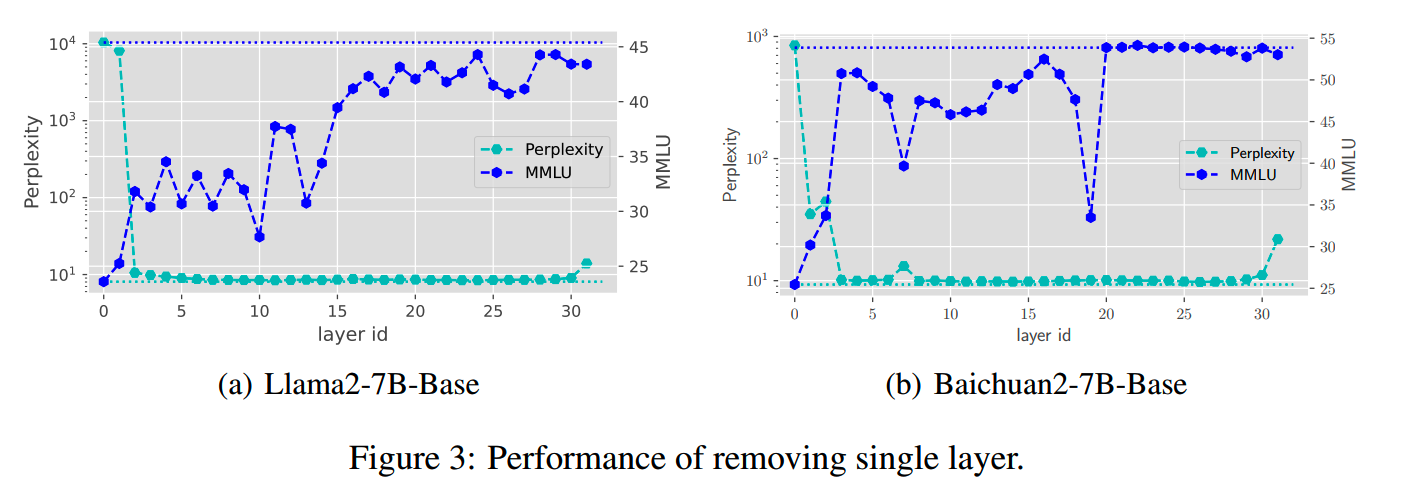
对于transformer模型，由于每一层的结构都一样，因此功能也类似，导致更容易出现层参数冗余的情况。对Llama2-7B-Base和Baichuan2-7B-Base移除某个层厚，看PPL和模型在MMLU上的变化，发现很多层其实对效果没有明显影响：

ShortGPT提出用下图的Block Influence计算每个层的重要性：

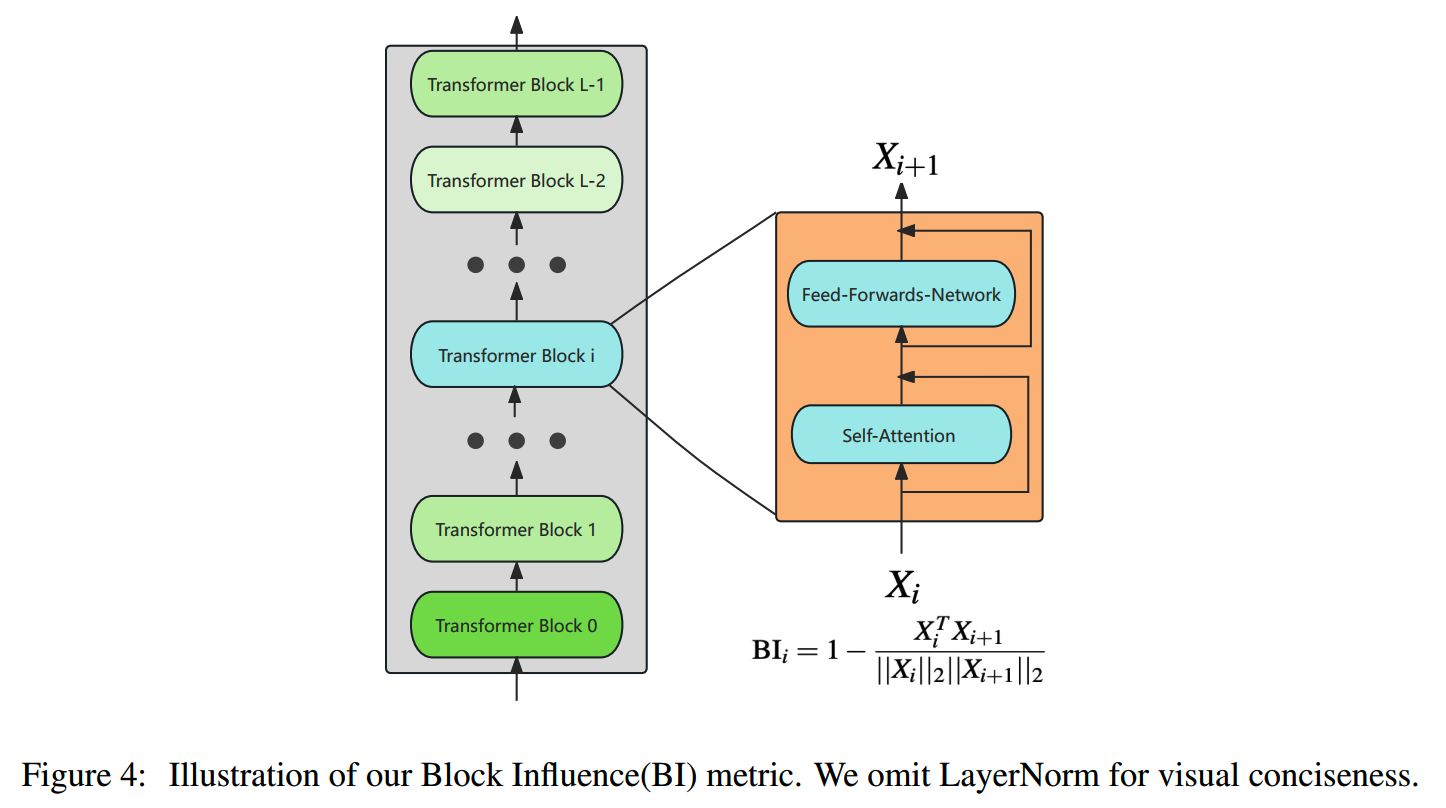
文中还对模型宽度的冗余情况也做了一下分析，发现和层的冗余一样，注意力头之间也有类似的冗余情况：

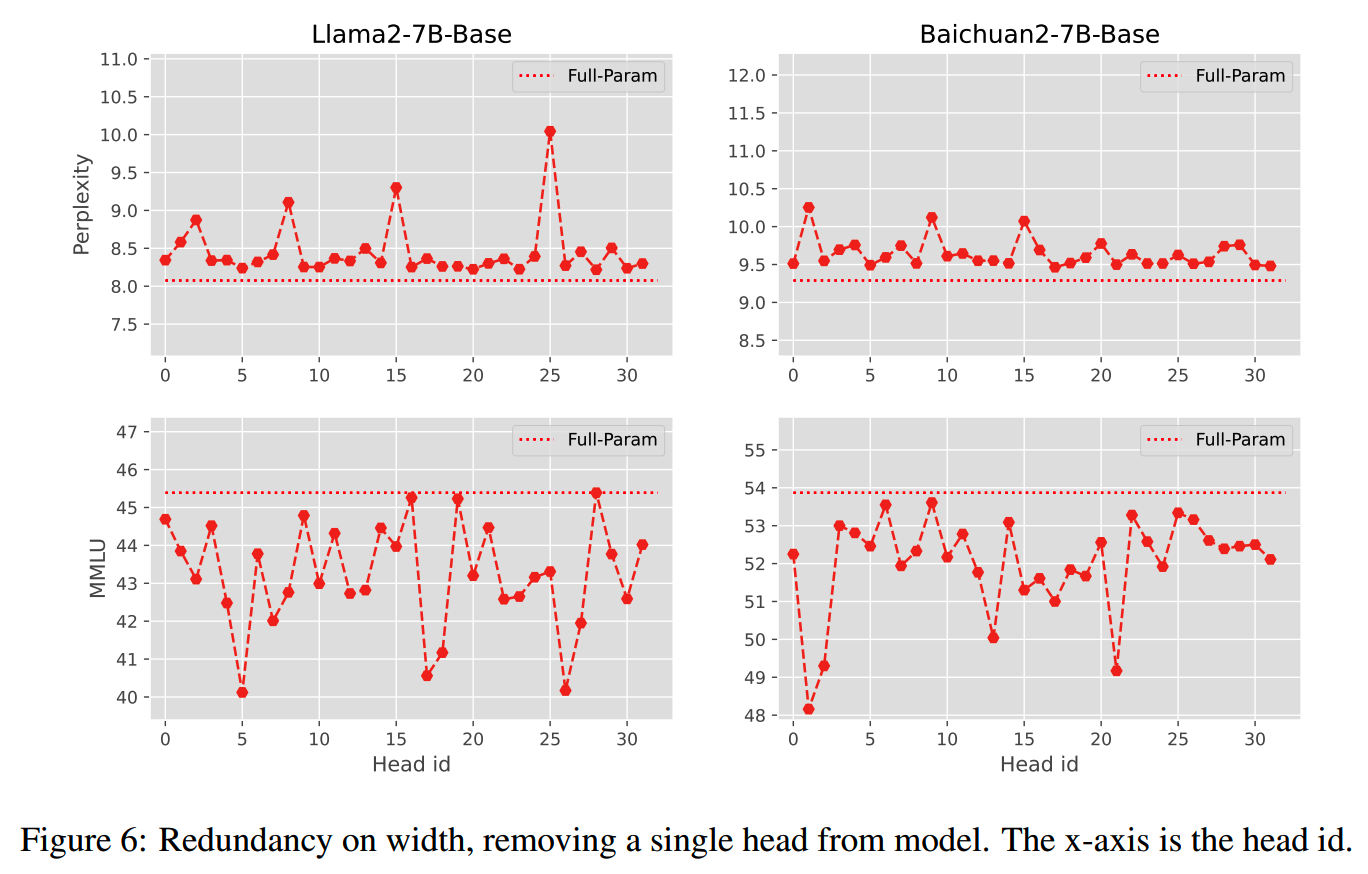
不过注意力头的冗余相比层数的冗余来说，没有那么明显的规律，不同的模型之间冗余模式有所不同。

Wanda

论文：《A Simple and Effective Pruning Approach for Large Language Models》

时间：2023年6月

Wanda = Weights and activations，Pruning by Weights and activations的意思。

Wanda其实并不算是模型裁剪的方法，因为在得到低重要性的参数之后，并没有将这些参数抛弃，而是保留稀疏化的参数矩阵/向量。不过因此Wanda也有一个好处，就是不需要重新训练模型，而通过稀疏化也能获得一定的推理加速效果。

简单来说，Wanda就是通过下图的方法计算参数重要性：

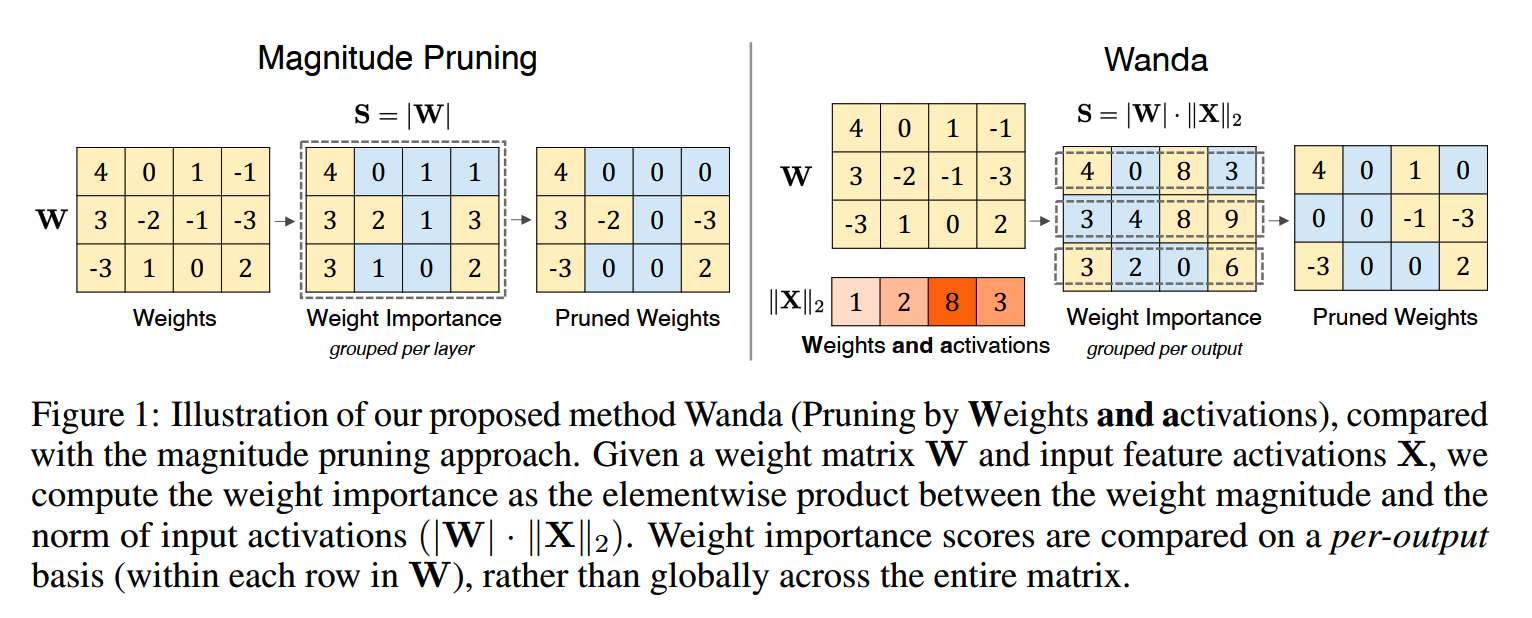
而稀疏度是作为超参输入的，实验中使用两种稀疏度设置：
- 4:8，对于每 8 个连续的权重，最多允许有 4 个非零权重。也就是说，在一个长度为 8 的连续权重块中，要剪掉至少 4 个权重，使得剩下的非零权重数量不超过 4 个。
- 2:4，意义和4:8类似。

PyTorch code for Wanda：

# W: weight matrix (C_out, C_in);
# X: input matrix (N * L, C_in);
# s: desired sparsity, between 0 and 1;
def prune(W, X, s):
  metric = W.abs() * X.norm(p=2, dim=0)
  _, sorted_idx = torch.sort(metric, dim=1)
  pruned_idx = sorted_idx[:,:int(C_in * s)]
  W.scatter_(dim=1, index=pruned_idx, src=0)
  return W

SLEB

论文：《SLEB: Streamlining LLMs through Redundancy Verification and Elimination of Transformer Blocks》

时间：2024年2月

SLEB尝试用三种metric对模型中transformer block的redundancy进行验证。

第一种metric是计算block的输入和输出之间的相似度。相似度越高，说明block的影响越小：

\[Metric_j^1=1-similarity(A_j,B_j)\]

\[similarity(x_i,x_j)=\frac{x_i\cdot x_j}{||x_i||||x_j||}\]

但是按这种方法移除block会导致PPL显著增加。原因是虽然一个block的影响可能很小，但是在inference的过程中，这个影响很可能被放大。

第二种metric则把要验证的transformer block移除，获取对输出结果的影响：

\[Metric_j^2=-\frac{1}{K}\sum_{k=0}^Klogp_{M_j}(w_k|w_{<k})\]

这种方法在PPL上的表现比第一种好，但是随着移除的层数增多，也会上升。

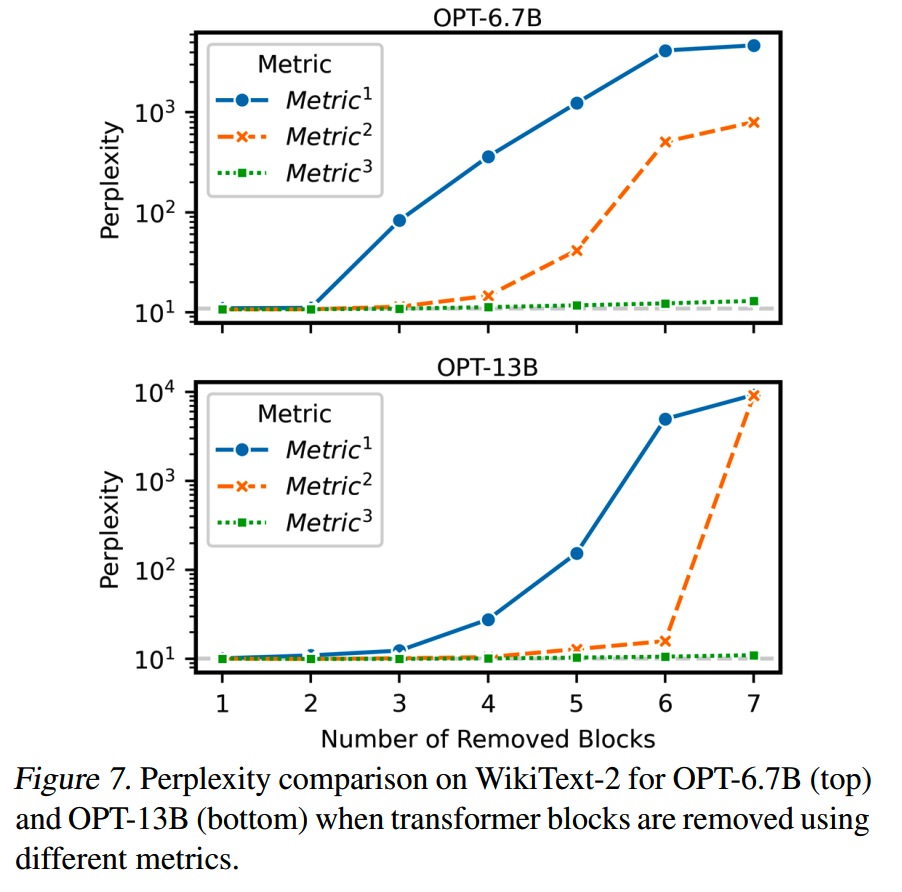
第三种metric其实和第二种一样，只是第三种metric是迭代移除block的。每次移除一层，并用移除后的模型作为base模型，用于下次的层重要性计算。

\[Metric_j^3(M')=-\frac{1}{K}\sum_{k=0}^Klogp_{M_j^{'}}(w_k|w_{<k})\]

M'就是上一次移除之后的result model。

第三种方法一定程度上避免了移除连续的层，从而更大程度保留模型的效果。

其他

一些文献：
- 关于模型neuron、attention head、层重要性的论文：《A survey on deep neural network compression: Challenges, overview, and solutions》、《An survey of neural network compression》、《A comprehensive survey of compression algorithms for language models》

博客：http://www.linsight.cn/
知乎：Linsight
微信公众号：Linsight
博主微信号(添加请注明来意)：

Reference

【1】Learning Sparse Neural Networks through L0 Regularization https://arxiv.org/abs/1712.01312
【2】Compact Language Models via Pruning and Knowledge Distillation https://www.arxiv.org/abs/2407.14679
【3】LLM Pruning and Distillation in Practice: The Minitron Approach https://arxiv.org/abs/2408.11796
【4】Shortened LLaMA: Depth Pruning for Large Language Models with Comparison of Retraining Methods https://arxiv.org/abs/2402.02834
【5】ShortGPT: Layers in Large Language Models are More Redundant Than You Expect https://arxiv.org/abs/2403.03853
【6】Laco: Large language model pruning via layer collapse https://arxiv.org/abs/2402.11187
【7】A Simple and Effective Pruning Approach for Large Language Models https://arxiv.org/abs/2306.11695
【8】SLEB: Streamlining LLMs through Redundancy Verification and Elimination of Transformer Blocks https://arxiv.org/abs/2402.09025