大模型偏好对齐-IPO
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
前面我们对DPO、ODPO、simPO的思路做了整理:大模型偏好对齐-DPO,大模型偏好对齐-ODPO,大模型偏好对齐-simPO。
而《A General Theoretical Paradigm to Understand Learning from Human Preferences》提出了可以将RLHF和DPO的目标函数视为其中一个特例的更general的目标函数ΨPO,并对ΨPO的一些问题进行了分析,最终设计了Identity-PO (IPO)来绕过这些问题。
ΨPO
回顾一下RLHF,它的目标函数是
\[\mathbb{E}_\pi[r(x,y)]-\beta D_{\text{KL}}(\pi\mid\mid\pi_{\text{ref}})\]
而DPO从等价的目标函数推导出DPO的损失函数如下
\[\begin{aligned}\min_{\pi}\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\Bigg[-\log\sigma\Bigg(\beta\log\Bigg(\frac{\pi(y_w|x)}{\pi(y_l|x)}\Bigg)-\beta\log\left(\frac{\pi_{\mathrm{ref}}(y_w|x)}{\pi_{\mathrm{ref}}(y_l|x)}\Bigg)\Bigg)\right]\end{aligned}\]
IPO这篇论文则提出一个general的目标函数。考虑一个对preference probability进行非线性变换的non-decreasing function Ψ
\[\Psi:\begin{bmatrix}0,1\end{bmatrix}\to\mathbb{R}\]
Ψ-preference optimisation objective定义为
\[\max_\pi\quad\mathbb{E}_{x\thicksim\rho}\quad[\Psi(p^*(y\succ y'|x))]-\beta D_{\mathrm{KL}}(\pi\mid\mid\pi_{\mathrm{ref}})\]
如果我们给Ψ一个具体定义,如下式
\[\Psi(q)=\log(q/(1-q))\]
那么在Bradley-Terry model的假设下,我们有
\[\begin{aligned} \mathbb{E}_{y'\thicksim\mu}[\Psi(p^*(y\succ y'))]& =\underset{y'\thicksim\mu}{\operatorname*{\mathbb{E}}}\left[\Psi\left(\frac{e^{r(y)}}{e^{r(y)}+e^{r(y')}}\right)\right] \\ &=\mathbb{E}_{y^{\prime}\thicksim\mu}[\log(e^{r(y)}/e^{r(y^{\prime})})] \\ &=\mathbb{E}_{y'\thicksim\mu}[r(y)-r(y')] \\ &=r(y)-\underset{y'\thicksim\mu}{\mathbb{E}}[r(y')] \end{aligned}\]
右边最终结果里的第二项可视为常数。除去这个常数,ΨPO的优化目标和RLHF的优化目标是等价的,同时也就和DPO的目标是等价的。
同DPO的做法一样,这里我们可以推出ΨPO在Bradley-Terry model下的解析解
\[\pi^*(y)\propto\pi_{\mathrm{ref}}(y)\exp\left(\beta^{-1}\mathbb{E}_{y^{\prime}\thicksim\mu}[\Psi(p^*(y\succ y^{\prime}))]\right)\]
我们把Ψ(q)的图像画出来,如下所示
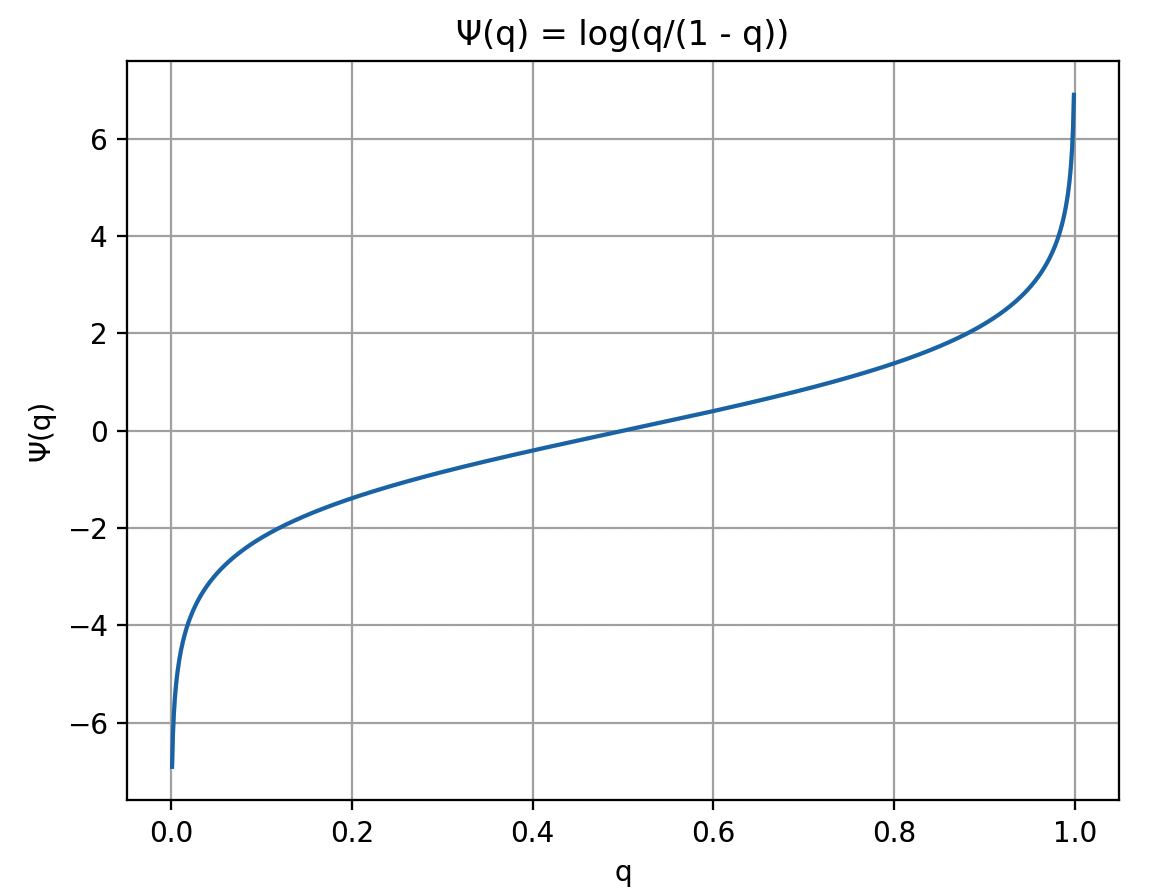
可以看到在两端,Ψ(q)的曲线有很强的非线性化特征,并且值会趋向于无穷大。
那么当我们对一对质量差异很大的样本,即
\[p^*(y\succ y')=1\]
进行学习时,在BT模型的假设下,就有
\[(r(y)-r(y'))\to+\infty\]
把 \((r(y)-r(y'))\to+\infty\) 代入到ΨPO上面退出来的解析解里,有
\[\begin{aligned} &\frac{\pi^*(y_l)}{\pi^*(y_w)}\\ =&\frac{\pi_{\mathrm{ref}}(y_l)}{\pi_{\mathrm{ref}}(y_w)}\mathrm{exp}\left(\beta^{-1}\sum_{y^{\prime}}[\Psi(p(y_l\succ y^{\prime}))-\Psi(p(y_w\succ y^{\prime}))]\right)\\ =&\frac{\pi_{\mathrm{ref}}(y_l)}{\pi_{\mathrm{ref}}(y_w)}\mathrm{exp}(\beta^{-1}\sum_{y^{\prime}}[r(y_l)-r(y_w)])\\ =&\frac{\pi_{\mathrm{ref}}(y_l)}{\pi_{\mathrm{ref}}(y_w)}\mathrm{exp}(\beta^{-1}\sum_{y^{\prime}}[-\infty])\\ =&0 \end{aligned}\]
那么此时无论 \(\beta\) 取什么值,都有 \(\pi^*(y_l)=0\)。说明当偏好越确定,KL项的约束能力越弱,模型就很容易摆脱KL项的约束,过度追求reward的最大化,最终导致过拟合。
不过RLHF在实践上并没有表现出如这里推算结果一样特别容易过拟合的特性,原因是因为训练出来的reward模型通常由于欠拟合,没有给出那么极端的偏好概率。反而是DPO因为节省了reward模型的训练,因此更加容易受到这种过拟合的困扰。
IPO
既然高度非线性化(且极值无限大)的Ψ(q)会导致DPO容易过拟合,那么一个自然的想法就是把Ψ(q)替换成一个有界的函数,identity mapping恒等变换就是一个符合要求的选择。这样就得到IPO的目标函数
\[\max_\pi\quad\mathbb{E}_{x\thicksim\rho}\quad[p^*(y\succ y'|x)]-\beta D_{\mathrm{KL}}(\pi\mid\mid\pi_{\mathrm{ref}})\]
根据这个,可以推导出IPO的损失函数为
\[\mathbb{E}_{(y_w,y_l,x)\thicksim D}\left(h_\pi(y_w,y_l,x)-\frac{\beta^{-1}}2\right)^2\]
\[h_\pi(y,y',x)=\log\left(\frac{\pi(y|x)\pi_{\text{ref}}(y'|x)}{\pi(y'|x)\pi_{\text{ref}}(y|x)}\right)\]
小结
ΨPO/IPO从理论上对DPO进行了一系列的分析,也推出了一个相对更不容易过拟合的偏好学习方法。不过在实践上的证明没有完善,可以作为一个理解的DPO的角度来参考吧。
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

【往期文章】
MoE模型的前世今生
LLM长上下文的问题
解锁大模型长上下文能力
大模型推理窗口-从有限到无限大
理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
大模型偏好对齐-DPO
大模型偏好对齐-ODPO
大模型偏好对齐-simPO
Yi技术报告-划重点看细节
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding
window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)
Reference
【1】A General Theoretical Paradigm to Understand Learning from Human Preferences https://arxiv.org/abs/2310.12036