transformer中normalization的二三事
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
Normalization在模型中,相对于attention这种经常被魔改的结构,受到的关注度似乎没那么高,但它对模型能否顺利训练,却有很关键的作用。
在此简单梳理下normalization相关的背景和内容,也分析一下在transformer发展上的相关内容。
这部分内容感觉目前还有些存在争议的地方,如果有不同意见欢迎讨论。
why normalization
normalization,也叫「归一化」、「正则化」、「规范化」、「标准化」等,可以说已经是神经网络不可以或缺的一环。
使用的话,现在基本只需几行代码就能实现。但要用得好,还是需要了解一下它作用的机制。
从输入数据看normalization
假设我们有一个二元损失函数 \(Loss(x_1,x_2)=x_1^2+x_2^2+b\) ,那在三维空间画出来的损失平面大概是这样
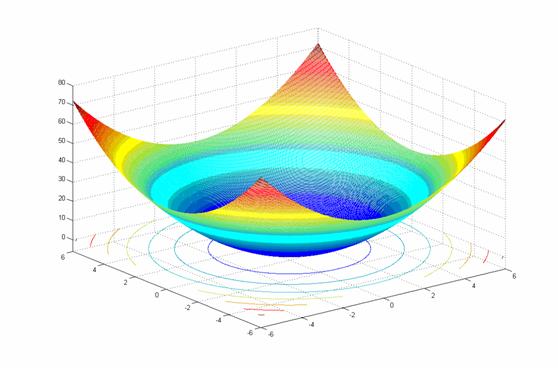
在这样一个平面上,使用梯度下降法,梯度方向是垂直于当前位置等高线的切线方向的。
如果这个损失函数的等高线是一系列完美的同心圆,那么无论我们起点在哪里,梯度下降的时候都会以垂直切线方向,沿着圆心一路奔去。
这种情况下优化很快,控制好学习率不要跳过minimum就可以(也可以用自适应优化器来控制速度)。
但是实际上我们的损失平面很难那么完美。损失函数的等高线更可能是个椭圆(或者更复杂的形状)。
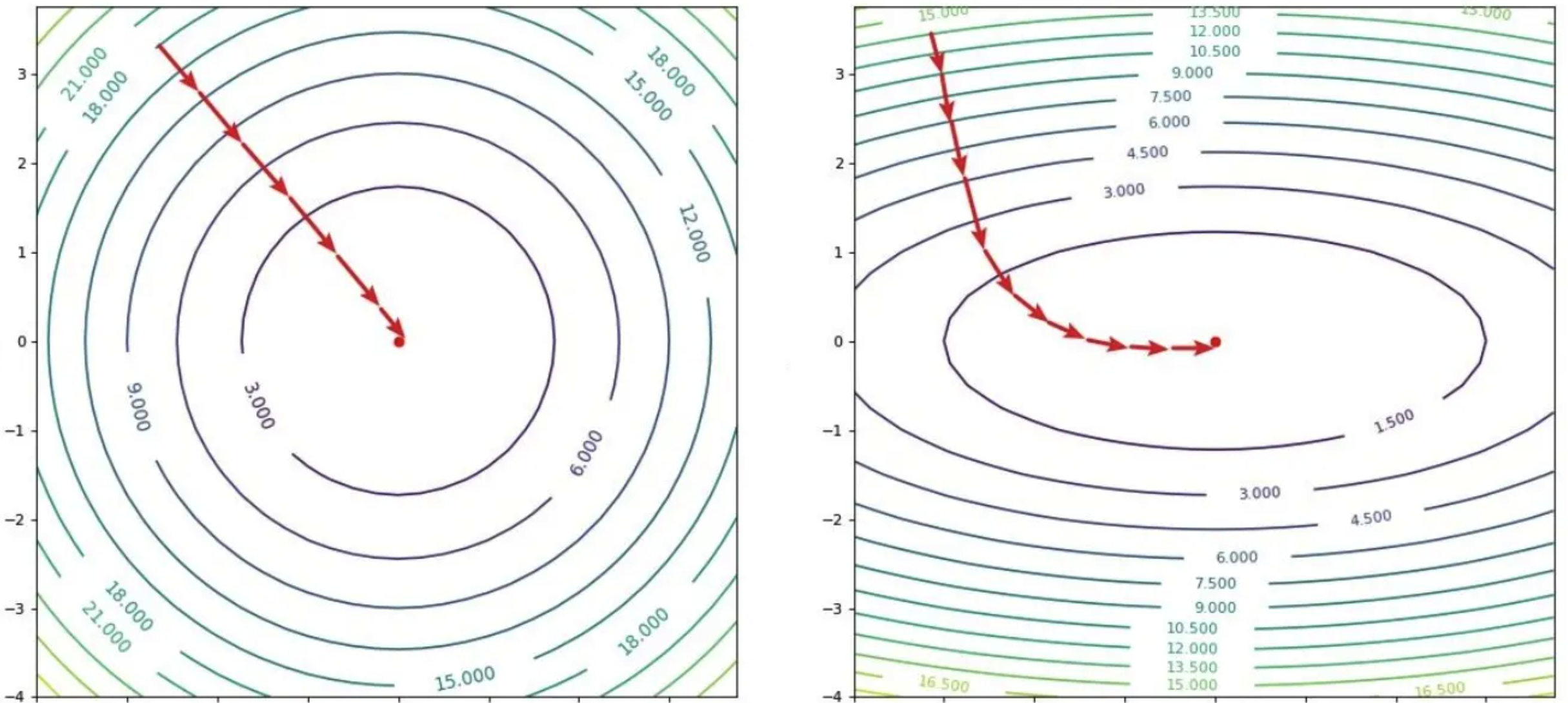
这样我们梯度下降是方向就要经常修正,训练效率就会受影响。
如果这个椭圆很扁或者我们的训练参数不太好,可能会出现反复震荡收敛缓慢的情况。
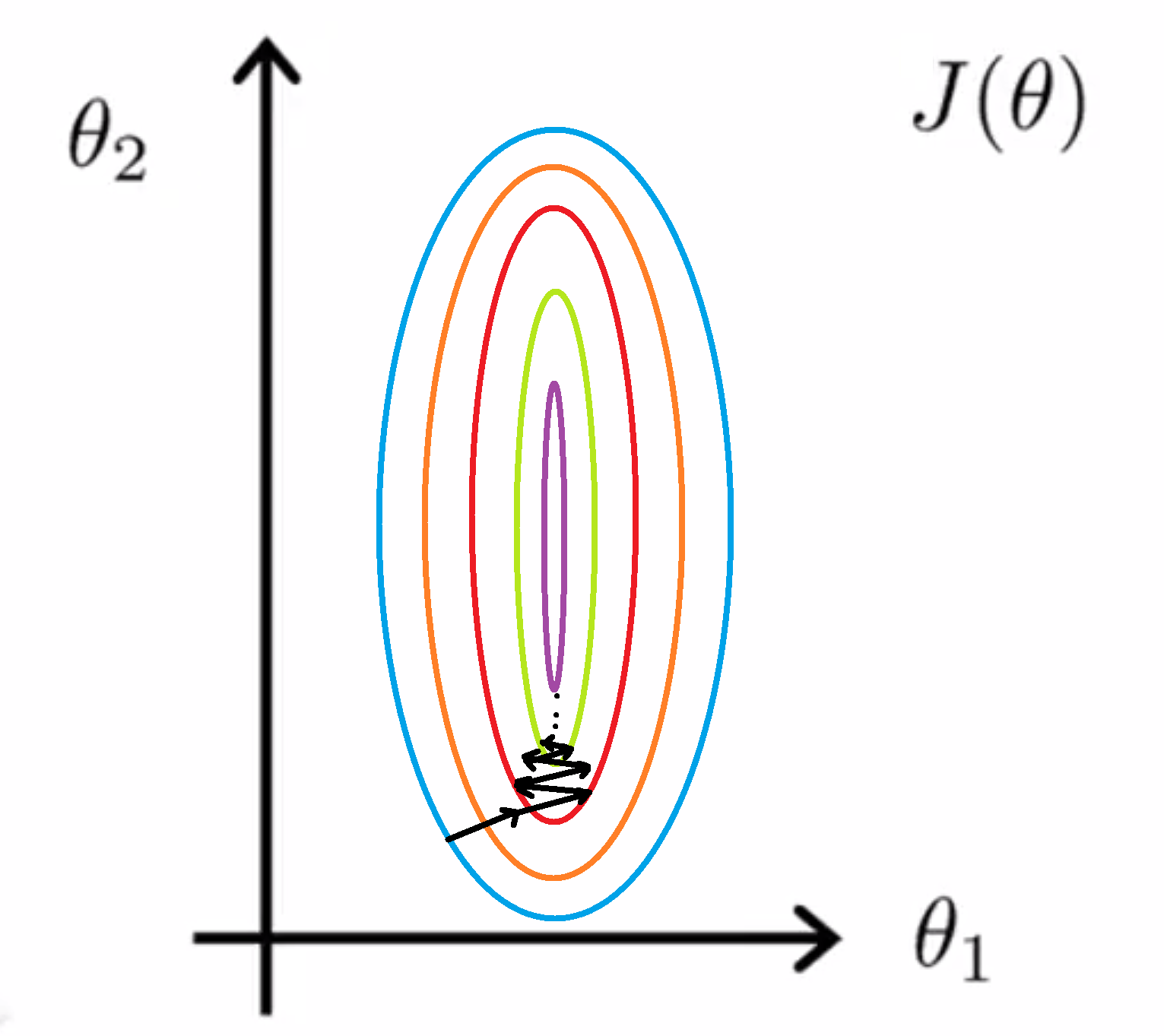
损失在这个狭窄的山谷中反复横跳。
那损失函数等高线什么时候会是椭圆形?
假设我们现在有两个输入变量,以米为单位的身高 \(x_{1}\),和以元为单位的月工资收入 \(x_{2}\)。(这里对量纲的使用也会改变数值,如米->厘米)
如果我们用这两个自变量训练模型,我们会发现,身高取值范围基本是在0.x米~2.x米,而工资的取值范围是0到几百几千几万或者几十万以及更多。
而模型的一个主要操作就是对输入特征进行线性组合。
这时模型的输出值会更大地受到 \(x_{2}\) 的影响,因为它的变化更大,取值范围也更大。
这时损失函数在不同变量维度的变化速度相差很多,损失函数就会出现椭圆形等高线的情况。
既然由于量纲和取值范围的问题,会导致训练困难,那最直接方法就是规定一个标准范围,所有输入变量,不管原来是什么范围,现在都归一化到标准范围里来。
这就是最朴素的输入normalization的思想。
输入的normalization有很多种做法
\[x^{\prime}=\frac{x-\min(\mathrm{x})}{\max(\mathrm{x})-\min(\mathrm{x})}\]
\[x^{\prime}=\frac{x-\mu}{\max(\mathrm{x})-\min(\mathrm{x})}\]
\[x^{\prime}=\frac{x-\mu}\sigma\]
其中 \(\mu\) 为均值,\(\sigma\) 为方差。
第三种,均值方差归一化,也叫Z-score normalization,应该是我们用得比较多的。
这样我们通过对输入进行一些操作,把「椭圆」拉成了「圆」,解决输入参数范围带来的一些训练问题。
除了针对均值、方差、最大值、最小值的归一化,对输入还有一些其他的处理,如PCA等,就暂不展开。
缓解ICS...吗?
机器学习里有一个叫i.i.d.(independent and identical distribution,独立同分布)的假设:独立,每次抽样之间是没有关系的,不会相互影响;同分布,即每次抽样,样本都服从同样的一个分布。
为什么需要i.i.d.?
由于机器学习依赖于使用现有数据来训练模型,进而对未来的数据做出预测和模拟,因此这一过程本质上是在历史数据的基础上,通过模型来推测未来的数据走向。
这就要求我们使用的历史数据必须具备整体的代表性。以便从现有数据(经验)中提炼出规律,对未知数据进行决策。
如果用于训练的数据缺乏总体代表性,即仅代表特殊情况,那么得出的规律可能不准确或错误,因为这些规律是基于个别案例推测出来的,就不具备泛化性。
当然并不是所有机器学习都需要i.i.d.,但是有i.i.d.的话,可以简化很多事情,让模型学习起来更容易快速。
对于输入,通过合理的抽样和处理(前面提到的PCA就可以用来解耦特征间的关联,达到“独立”的效果),我们可以得到输入的i.i.d.的条件,但这只是针对输入。
在多层的神经网络中,上一层的输出会作为下一层的输入。
而在训练过程中,由于上层的模型参数在不断学习变化,则上层输出的分布也在不断变化,靠后的层实际上要学习不断的变化的分布,这就很不i.i.d.,那靠后面的层的学习速度和效果就会收到影响,调参也变得困难,模型也难以加深。
这个问题就是ICS,internal covariate shift。
那有没有办法保证上一层的分布不要变化呢?
一个「可能」的方案就是normalization。我们通过把上一层的输出映射到一个固定的分布上,来稳定给下一层的输入,这样就降低了学习难度。
但也有一些工作表明normalization(batchnorm)的作用机制和ICS的关系并不大,这个观点下面在batchnorm部分说。
当然ICS的问题也可以通过改变初始化策略、调控训练超参如学习率等方法来优化,但是这样做的效率并不是很高。
远离激活函数饱和区
神经网络中还有一个重要组件,非线性激活函数,比如常用的sigmoid。
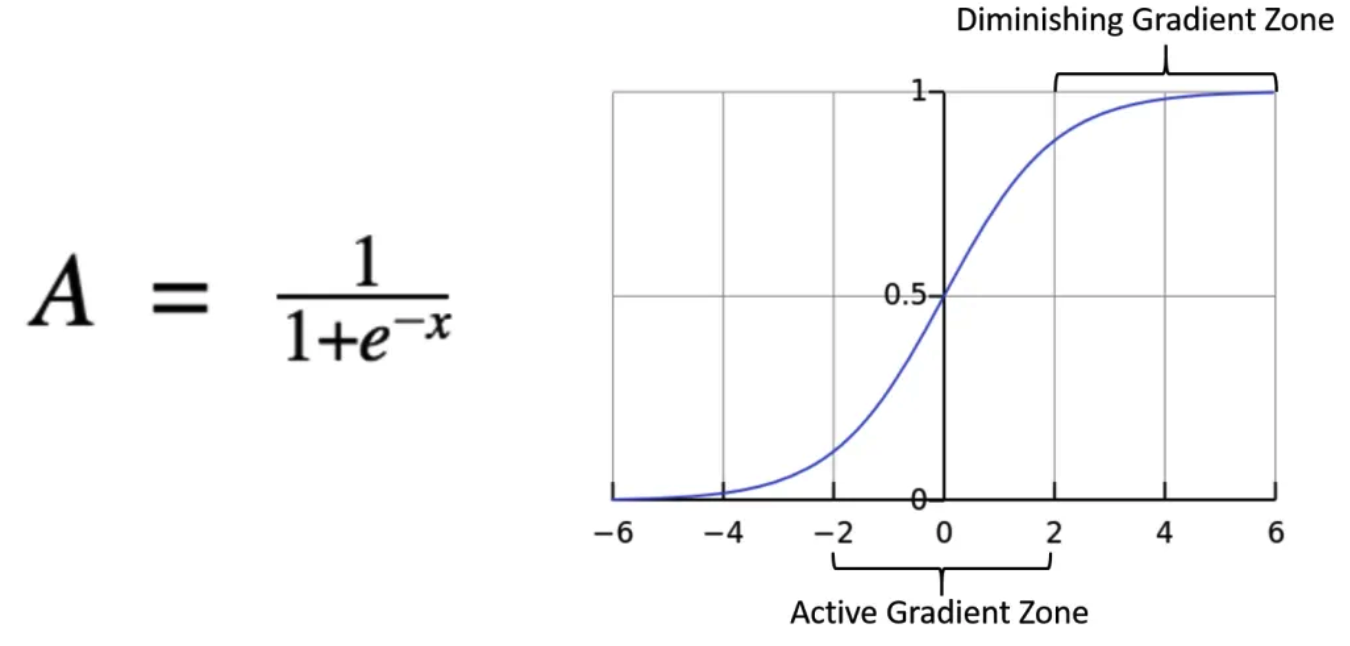
当输入 > 6 或者 < -6 的时候,sigmoid函数的梯度已经变得非常小,也就是进入了饱和区。
这种情况下训练就变得困难。
ICS就会加剧梯度消失的情况。在没有normalization的情况下,分布不断变化,后面层的参数变化激烈,导致输出值更容易进入到左右两端,更容易进入到激活函数的饱和区。
而normalization能把部分输出值拉回到梯度正常的范围内,一定程度缓解了梯度消失的问题,使训练可以正常进行下去。
batchnorm
神经网络中使用的normalization有很多种,这里不一一展开,只梳理一下最重要的batchnorm和layernorm两类。
batchnorm算法
假设输入数据的形状是 \([B,C]\) ,其中 \(B\) 是batch size,\(C\) 是特征向量维度。
这 \(C\) 个输入特征每个都有不同的含义,如我们前面的例子,第一个元素可能是身高,第二个元素可能是月收入,因此做normalization的时候这 \(C\) 个特征分别来做。
具体来说,对于第 \(i\) 个特征维度,首先计算整个batch内的均值
\[ \mu_{i}=\frac{1}{B}\sum_{j=1}^{B}x_{i,j} \]
再计算这个维度上的方差
\[ \sigma_{i}^{2}=\frac{1}{B}\sum_{j=1}^{B}(x_{i,j}-\mu_{i})^2 \]
得到均值和方差之后,对batch内维度上的所有值进行Z-score normalization
\[ x_{i,j}'=\frac{x_{i,j}-\mu_{i}}{\sqrt{\sigma_{i}^{2}+\epsilon}} \]
其中 \(\epsilon\) 是为了防止分母为0。这个在实际代码中挺重要的,忘记加可能会出问题。
经过这样的变换之后,在 \(C\) 个特征维度上就是均值为0,方差为1的分布了。
但是到这还没结束。
每个维度的数值全部归一化之后,对于激活函数来说,更集中在中间的部分,而这部分的非线性特征并不强(比如上面的sigmoid),这样非线性激活层近似了一个线性变换,这样就降低了模型的学习能力。
且无论输入是什么,最终输出都会被强行拉到这样一个“平均”的值,也极大抑制了模型的表达能力。
所以为了保证模型的能力,也保证非线性能力的获得,对每个特征,又增加两个可学习的参数, 缩放参数 \(\gamma\) 和位移参数 \(\beta\) 。
\[ y_{i,j} = \gamma_{i} x_{i,j}' + \beta_{i} \]
这样每个特征值就有机会从“线性区”移动到“非线性区”,把被归一化削弱的非线性能力找了回来。
并且通过这样一个归一化再重新缩放移动的操作,解耦了上层输出分布和下层输入,本来下层参数要去适应上层分布变化,现在只需要通过每个batchnorm层中的 \(\gamma\) 和 \(\beta\) 直接学习就行了,训练变得简单了。
《Batch Normalization: Accelerating Deep Network》给出的算法如下

CNN中的batchnorm
batchnorm最主要的应用还是在CNN模型中。
假设CNN中feature map的size是 \([B,C,H,W]\) ,其中 \(B\) 是batch size,\(C\) 是channel数(也是卷积核数量),\(H\) 和 \(W\) 分别是特征图的高和宽。
如果按照前面batchnorm的算法,那应该有 \(C\times H\times W\) 组特征,每组特征有 \(B\) 个,对每组内的 \(B\) 进行归一化,再进行放缩和平移。
但是实际上,CNN中卷积是一个滑动窗口,对于同一个channel下的 \(H\times W\) 个特征值其实都来自于同一个卷积核的计算,这 \(H\times W\) 也属于一个“batch”,它们要放在一起进行归一化。
也就是对于卷积核来说,真正的batch数是 \(B\times H\times W\) ,而只有 \(C\) 组特征值,因此也只有 \(C\) 个 \(\gamma\) 和 \(\beta\) 。
batchnorm原文中,batchnorm放在了relu后面,作者认为这样使得进入激活函数的分布会更加稳定,顺便对于fc层,由于batchnorm和fc都有bias项,还可以省略掉其中一个而不影响效果。
btw,一般来说,batchnorm初始化的时候,把 \(\gamma\) 设为1(不缩放),把 \(\beta\) 设为0(不平移),在训练中让模型从相当于没有batchnorm开始慢慢学习这两个参数。
训练和推理
现在我们知道在训练时,batchnorm对一个mini-batch计算均值和方差来进行归一化,再进行缩放和移动。
\(\gamma\) 和 \(\beta\) 属于模型学出来的参数,只要训练结束这两个向量就固定了,在推理的时候直接使用即可。
但是推理时,均值和方差怎么计算呢。推理的时候可能是一个sample,也可能是任意个sample作为一个batch,和训练的时候一样计算肯定不合适。
我们需要在训练的时候就为推理做准备:训练的时候,模型会遍历整个训练集,因此理论上可以统计出整个训练集的均值和方差,然后把这个大量样本统计出来的均值和方差当做真实分布的均值和方差,在推理的时候使用。(回想i.i.d.)
当时又有一个问题,训练集可能会很大,有百万甚至千万的数据,在训练的数据记录下所有层所有特征来计算均值和方差显然效率不高,因此用一个近似的方法:
moving_mean = momentum × moving_mean + (1.0 − momentum) × mean
moving_var = momentum × moving_var + (1.0 − momentum) × var
通过把多个batch的均值和方差进行移动平均的方式来逼近整个训练集的均值和方差。
momentum为动量参数,在 TF/Keras 中,该值为0.99,在 Pytorch 中,这个值为0.9。
小的momentum值对应快的更新速度,能够更快地向真实分布靠近,但是同时也会导致更大的波动。
大的momentum值对应慢的更新速度,如果更新过慢,则可能导致训练结束时还没有统计到真实的分布,是欠拟合的状态。
如果batch size比较小,每个mini batch和全局差异较大,就不应该用太大的momentum。
理论上,训练步数越长是会越靠近真实分布的,实际上,因为每个batch并不能代表整个训练集的分布,所以最后的值是在真实分布附近波动。
这里还引入另外一个问题,如果batch size太小,每个mini batch统计的均值和方差和全局的值偏差相对会比较大,对模型收敛的稳定性有影响,因此一般来说,使用batchnorm的话,batch size不能太小,如下图
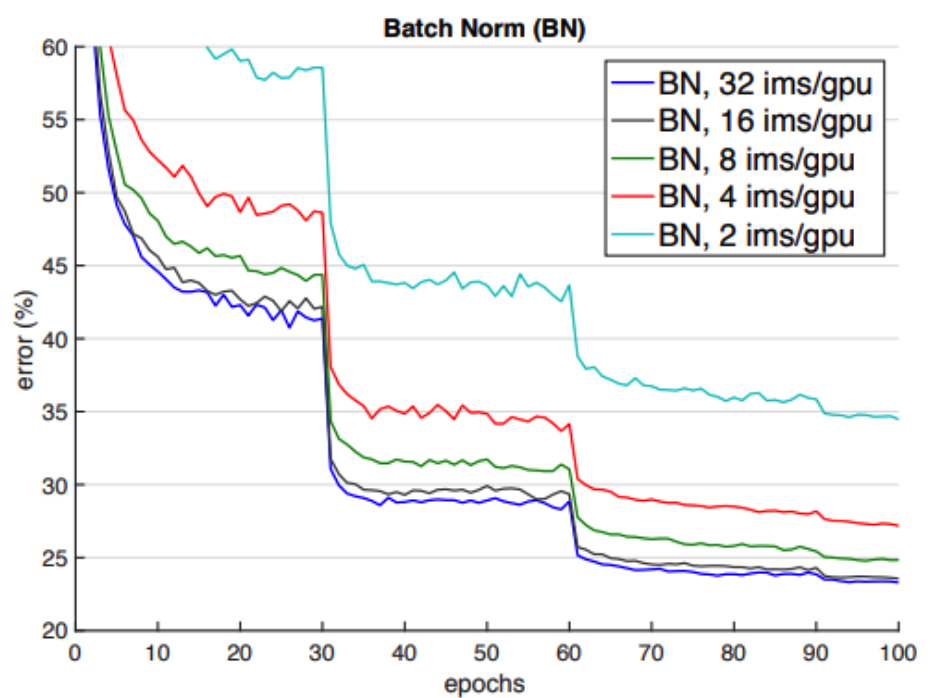
小结一下,batchnorm的优点是解耦了上层输出和下层输入的分布,既缓解了进入激活函数饱和区带来的梯度消失的情况,又保留了模型的表达能力。每一层的输入尺度相对固定,提供了更好的尺度不变形,使模型训练更稳定。
同时每个batch分别进行归一化,相当于引入了一些随机噪音,使得模型不容易过拟合到某些微小的特征上,相当于进行了一定的正则化,将损失平面变得相对平滑。
但是同时也引入了新的超参(如momentum),另外也依赖batch size的大小,过小的batch size可能会带来问题。
batchnorm起作用的真正原因?
虽然batchnorm原文认为batchnorm在一定程度上是缓解了ICS,但是2018年的《How Does Batch Normalization Help Optimization?》提出了不同观点。
为了探究batchnorm的效果,是否是因为优化了ICS(或者说和优化了ICS有多大关系),做了一个这样的实验:在batchnorm后面又通过加入随机噪音来引入“covariate shift”,并和没有加噪音,以及没有加batchnorm的模型效果进行对比,如下图
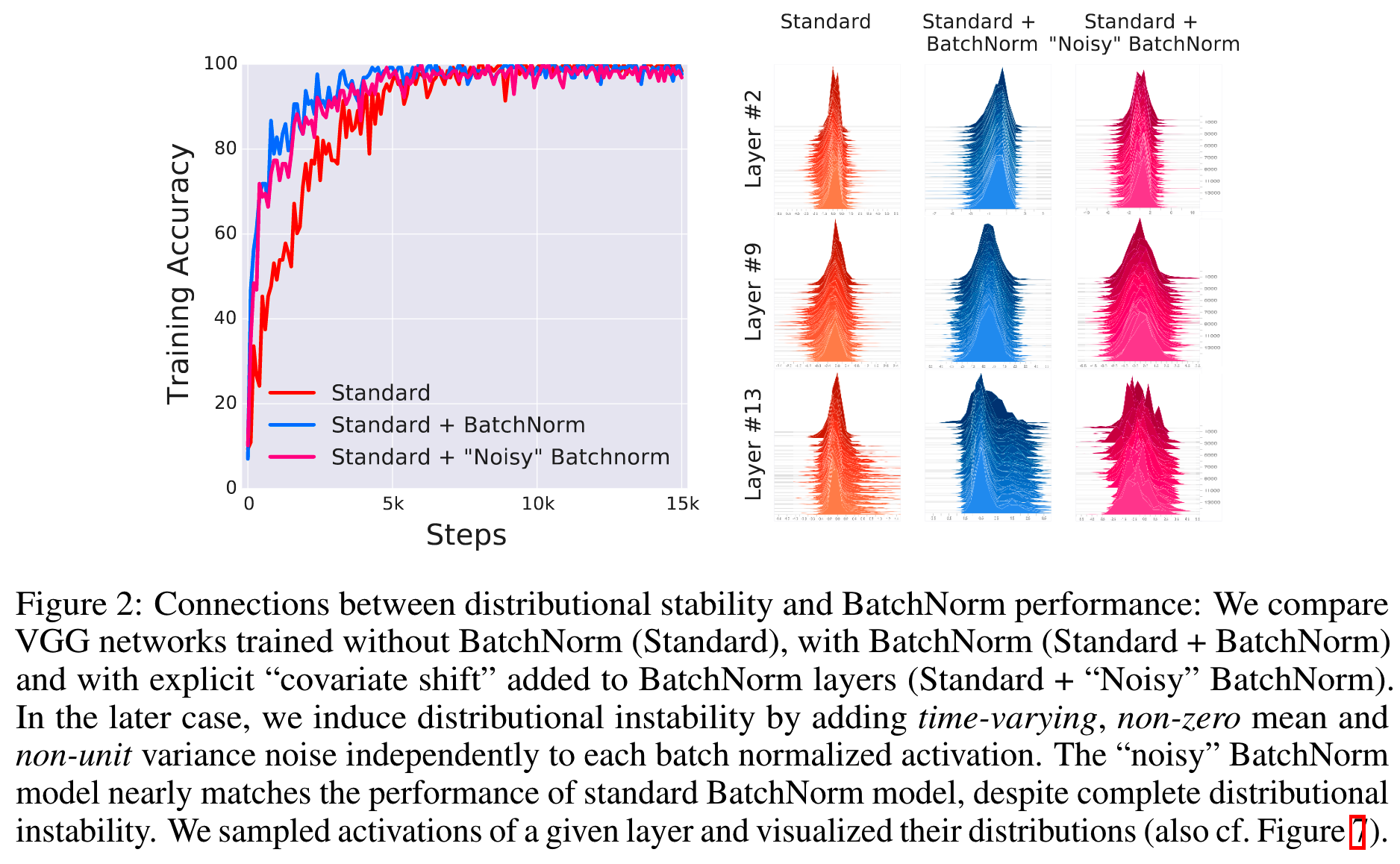
结果发现,即使人工加强了ICS的情况,但是只要用了batchnorm,效果依然比不用好;而人工引入ICS的模型,在效果上并没有多大影响。
这就说明缓解ICS并不是batchnorm有效的真正原因。
那batchnorm到底有没有缓解到ICS呢?
要测量ICS的变化,就要先定义ICS。
对于网络中的每一层,ICS被定义为在前一层参数更新后,当前层输入分布的变化。这种变化可以通过比较更新前后的梯度来量化。

具体来说,对于每一层i,作者们计算了以下两个梯度之间的L2范数差异:
\(G_{t,i}\) ,在时间t,使用当前所有层的参数(包括前一层的参数)计算的梯度。
\(G_{t,i}'\) ,在时间t,使用更新后的前一层参数计算的梯度,而其他层的参数保持不变。
这个差异直观上表明了「上一层参数变化,下一层需要在多大程度上来变化,以适应新的分布」。
理想来说,ICS越小,上一层参数更新对当前层的分布影响越小,梯度变化程度应该越小。
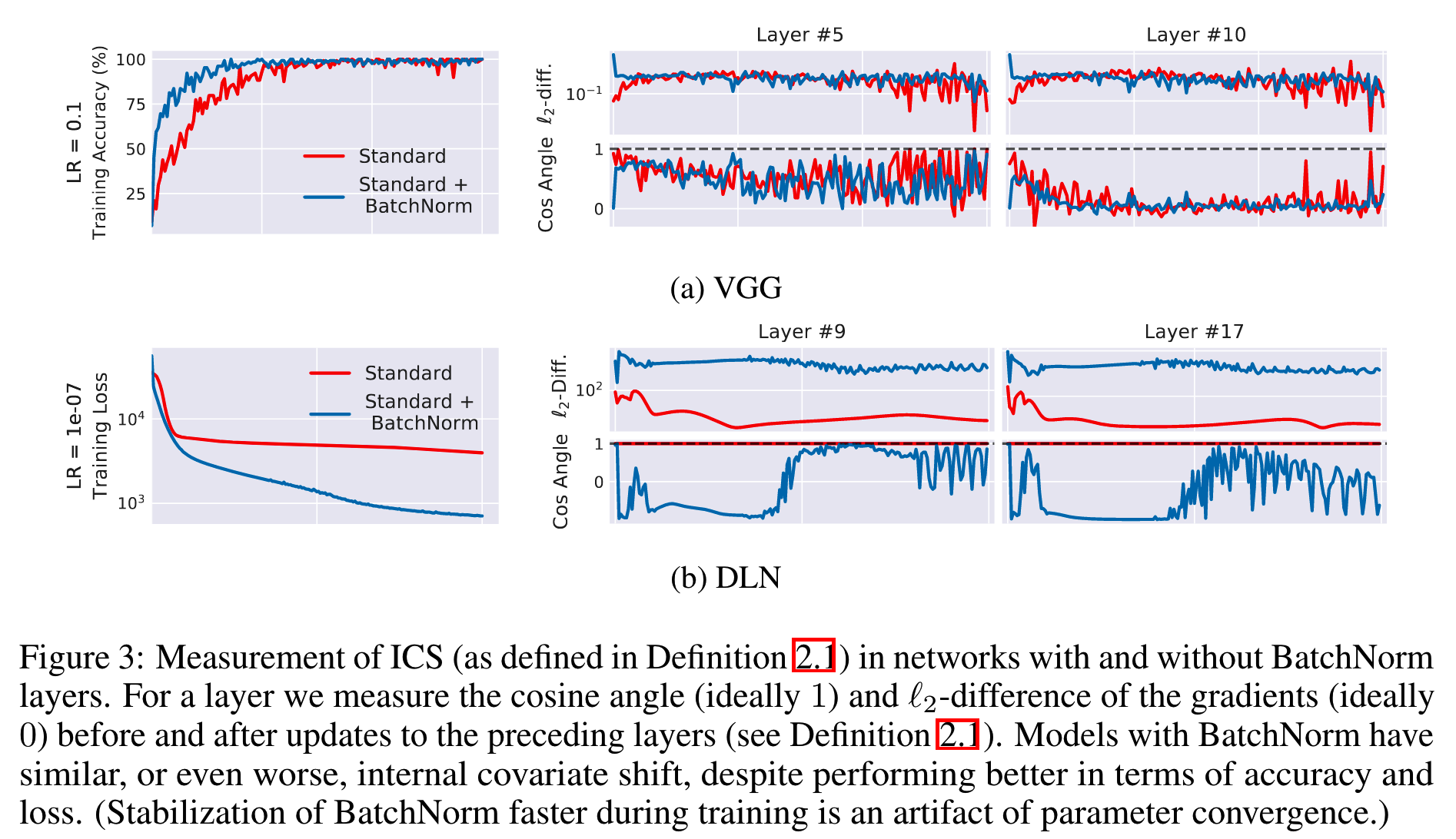
但是从结果上来看,使用了batchnorm并不能有效减少这个变化,甚至还有所增加。
这也说明batchnorm实际上并不能真正缓解ICS的情况。
那batchnorm起效果的真正原因是什么?
作者认为主要是batchnorm使得损失函数更加平滑,直观上来说就是减少了很多坑坑洼洼的位置,使得训练更不容易陷入到局部最小值中去。
layernorm
看完batchnorm,再来看layernorm。
理解layernorm
layernorm,不要被名字骗了,这里的layer指的不是模型的层,而是数值的layer。
对于二维的输入,batchnorm实在batch维度上做归一化,而layernorm是在特征维度做归一化
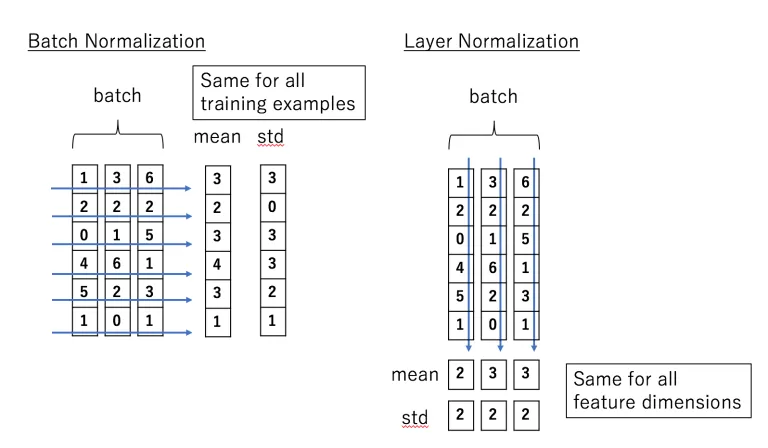
对于非NLP数据而言,相比batchnorm,layernorm归一化的维度似乎解释性没那么强。batchnorm对同一个特征,比如身高计算均值是有意义的,而layernorm在不同的特征,比如身高、工资、温度做归一化,好像并没有可靠的物理意义。
layernorm最主要的应用就是NLP的模型,包括RNN和transfomrer模型。
在transformer中,一般输入的形状是 \([B,S,H]\) ,\(S\) 是序列长度,每个样本的长度可能不同,因此在这个维度需要使用padding(一般是zero-padding)来把batch内的数据处理成一样长。
比如这样一批文本输入
1 | 我 爱 中 国 |
为了使模型能够统一处理,会pad成
1 | 我 爱 中 国 |
一般来说,我们认为由于有padding的存在,做batchnorm并不合适。
比如上面的例子,对“中”,“[P]”,“你”做归一化,由于 [P] 的存在,实际的batch size只有2,并且和 [P] 做normalization也对训练没什么帮助。
而且对于文本数据,batch内同一个位置上的字是不同的,对完全没有关系的字进行归一化也并没有什么意义。
也就是说,哪怕没有 [P] 的存在,比如对第一个token“我”,“你”,“谢”做归一化,直觉上也不太有物理意义。
因此使用layernorm,在 \(H\) 维度上进行normalization,同时有 \(H\) 个\(\gamma\) 和 \(\beta\) 需要学习。
相当于计算每一句输入内,每个token所有特征之间的均值和方差来进行归一化。
为什么transformer用layernorm
和batchnorm不同的是,由于layernorm不需要再batch维度上计算均值和方差,所以不存在训练和推理的时候不一样的地方,不用保存一个全局的均值和方差供推理的时候使用。
而由于layernorm和batch无关,也就不会受到batch size大小的影响。
除了以上的原因,也有一些工作深入探究了在nlp任务上layernorm和batchnorm的区别。
如《PowerNorm: Rethinking Batch Normalization in Transformers》就研究了transformer中BN为啥表现不太好。
研究了训练中的四个统计量:batch的均值和方差,以及他们的梯度的均值和方差。对于batch的均值和方差,计算了他们和running statistics(就是用移动平均法累积的均值和方差,见前面的文章)的欧氏距离。发现NLP任务上(IWSLT14)batch的均值和方差一直震荡,偏离全局的running statistics,而CV任务也相对稳定。
对于他们梯度的均值和方差,研究了其magnitude(绝对值),在CV任务上震荡更小,且训练完成后,也没有离群点。
总结来说,transformer中BN表现不太好的原因可能在于CV和NLP数据特性的不同,对于NLP数据,前向和反向传播中,batch统计量及其梯度都不太稳定。
更重要的是,实际效果就是layernorm在NLP的效果比batchnorm好,效果好,这是最重要的原因。
RMSnorm
19年《Root Mean Square Layer Normalization》提出了normalization变体RMSnorm,主要针对layernorm来改进。
简单地说,RMSnorm就是在标准layernorm的基础上,省略了平移,只进行缩放。

作者认为标准layernorm计算效率并不高
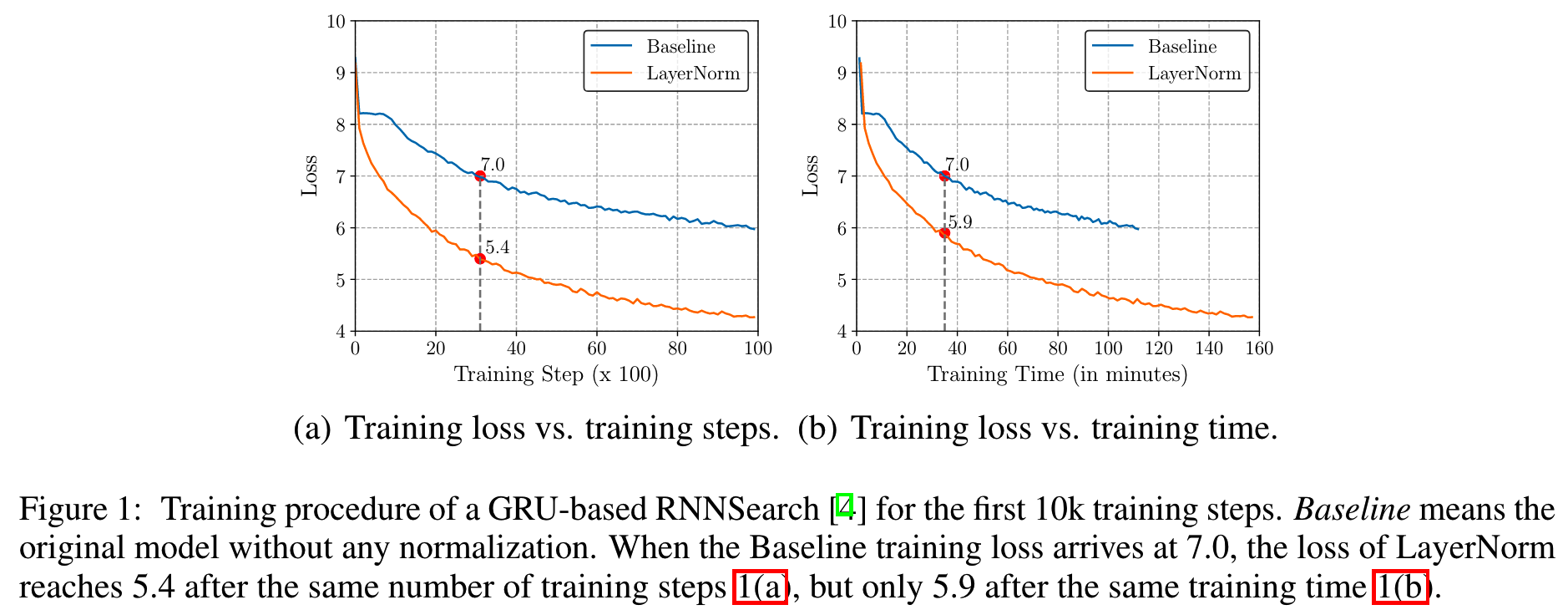
作者用一个GRU模型做实验,对比是否添加layernorm的结果,发现在相同时间和相同步骤下,有layernorm的模型,都没有无layernorm的模型收敛得快。
并且layernorm的平移对梯度方差的减小没有贡献,因此作者直接舍弃了中心化和平移两步,只对数据进行方差归一化和缩放。
更近一步,作者提出pRMSnorm,只对数据中前p%的数值进行处理,这样就能进一步加速训练,而效果也基本不太受影响。
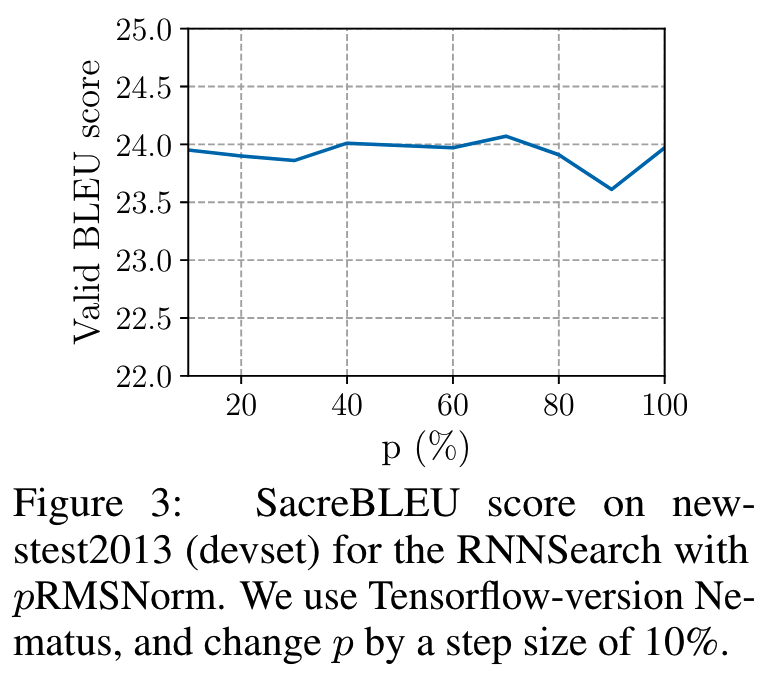
RMSnorm现在被很多主流的大模型所采样了。
post-norm & pre-norm
二者对比
layernorm在模型里放哪也有讲究。
原始的transformer模型使用的post-norm,而《On Layer Normalization in the Transformer Architecture》则认为pre-norm更好。
post-norm和pre-norm分别是下面这样
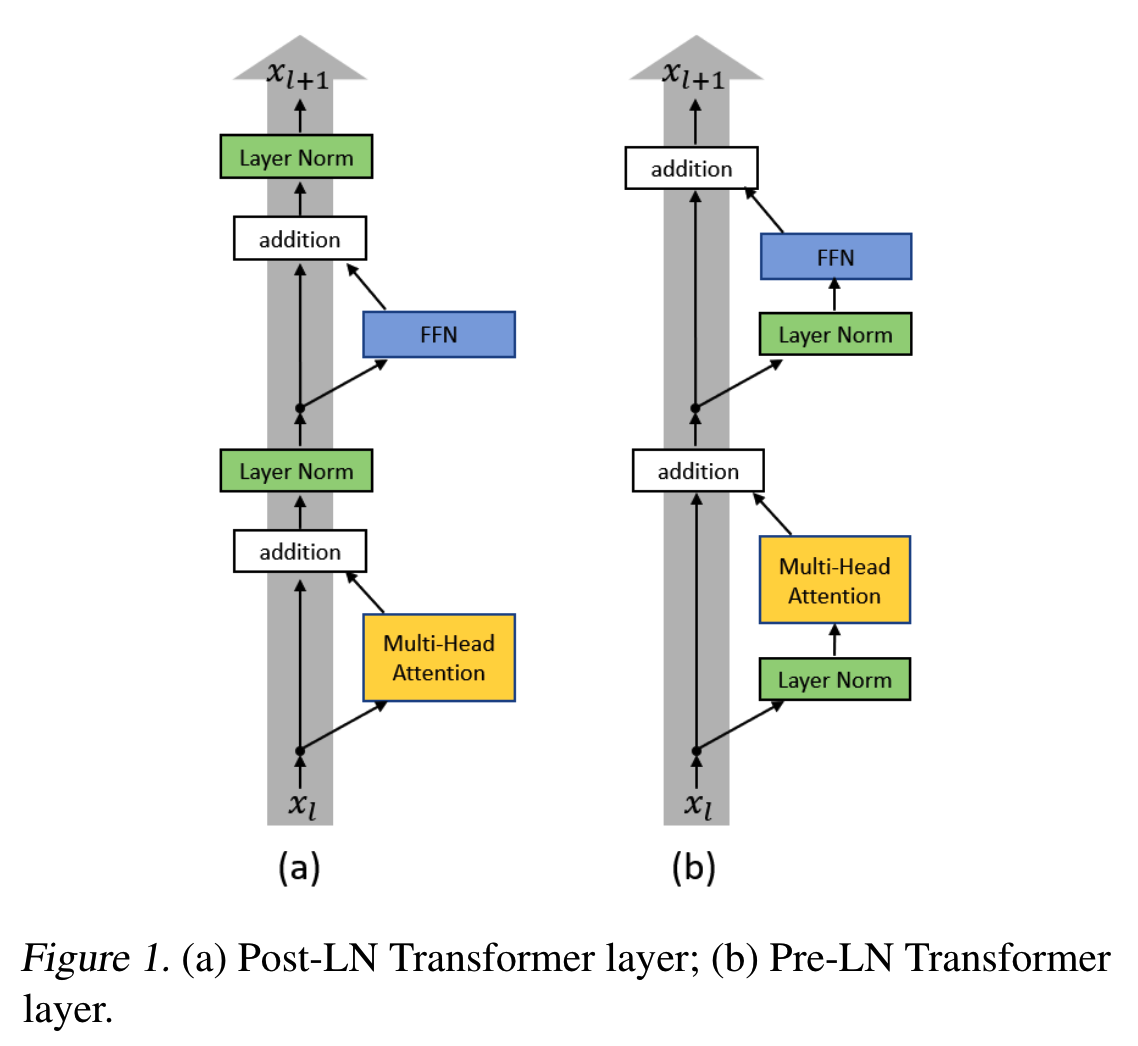
post-norm是在残差和主干相加之后进行归一化,而pre-norm则是在主干先归一化再和残差相加。
post-norm和pre-norm对比,目前大家比较接受的结论是,pre-norm更容易训练,因此可以叠加更多的层,但是在层数不是特别多的情况下,post-norm最终的收敛效果会比pre-norm要好。
模型中,第 \(l\) 层的输出是第 \(l+1\) 层的输入,对于post-norm有
\[ x_{l+1}=\mathrm{Norm}(x_l+\mathrm{F}_t(x_l)) \]
而对于pre-norm则是
\[ x_{l+1}=x_l+\mathrm{F}_l(\mathrm{Norm}(x_l)) \]
参考苏剑林在《为什么Pre Norm的效果不如Post Norm?》中的分析,认为 \(\mathrm{F}_l(\mathrm{Norm}(x_l))\) 的方差,由于有norm的存在,是不随层数变化的。
当 \(l\) 比较大时,\(x_{l}、x_{l+1}\) 的差距较小,因此 \(\mathrm{F}_l(\mathrm{Norm}(x_l))\) 和 \(\mathrm{F}_{l+1}(\mathrm{Norm}(x_{l+1}))\) 的差距也很小,这时有
\[\begin{aligned} &\mathrm{F}_l(\operatorname{Norm}(x_l))+\operatorname{F}_{l+1}(\operatorname{Norm}(x_{l+1})) \\ &{\approx}\mathrm{F}_l(\mathrm{Norm}(x_l))+\mathrm{F}_{l+1}\left(\mathrm{Norm}(x_l)\right) \\ &=(\mathrm{F}_l\oplus\mathrm{F}_{l+1})(\mathrm{Norm}(\pmb{x_l})) \end{aligned}\]
相当于 \(l\) 层和 \(l+1\) 层的效果接近于一个更宽的 \(l\) 层的效果。
也就是使用pre-norm的时候,模型的深度有水分,表面看起来有 \(l\) 层,实际在效果上,等效于post-norm的浅层模型。
从模型结构上看,恒等分支永远有一部分不用经过normalization,这部分能够直接把梯度回传到最前面,这也是pre-norm能够训练“层数更多”的模型的原因--缓解了梯度消失。
正常来说,模型深度对最终效果的影响,是大于模型宽度的。
而post-norm,在残差分支之后做归一化,对参数正则化的效果更好(loss平面更平滑),且它每norm一次就削弱一次恒等分支的权重,所以post-norm相对pre-norm,是更突出残差分支的,因此它的层数更加“足秤”,训练好之后效果更优。
和warmup的关系
《On Layer Normalization in the Transformer Architecture》(认为pre-norm更好)还分析指出,使用post-norm的transformer,在初始化时候,靠近输出层的部分梯度期望很大,所以模型在开始训练的时候很依赖warmup的策略,通过缓慢提升学习率来稳定训练过程。
使用warmup引入了新的超参,调参更为麻烦点。
而实验表明,使用pre-norm的transformer在不需要warmup的情况下,也能收敛到post-norm+warmup的相同水平,而post-norm不加warmup效果就差点了。
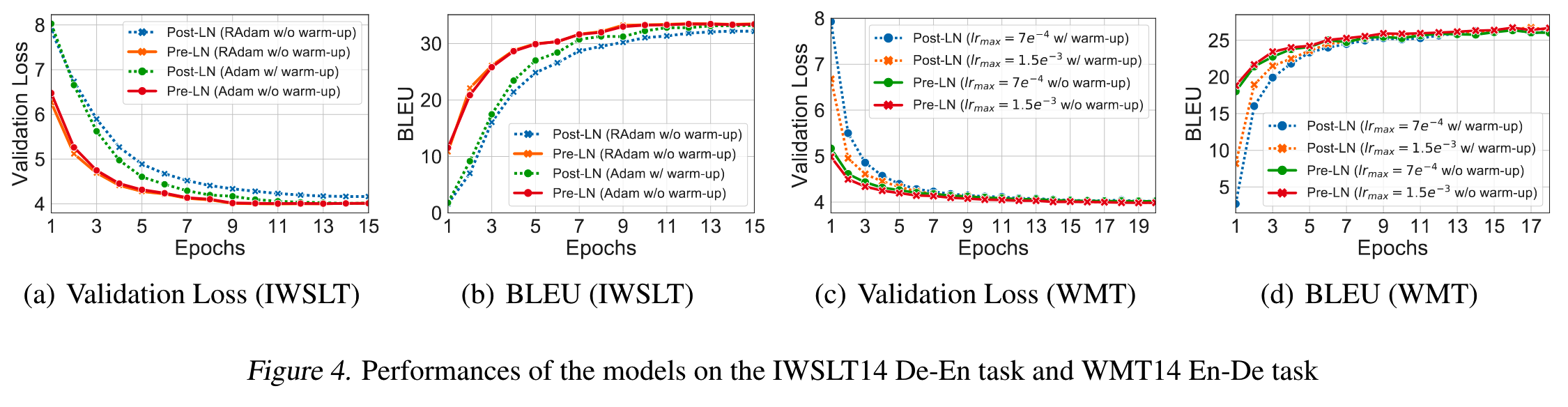
Deepnorm
2022年,《DeepNet: Scaling Transformers to 1,000 Layers》对transformer训练不稳定的原因进行了深入分析,发现模型更新过大是导致不稳定的主要原因。
为了解决这个问题,他们提出了Deepnorm,可以限制模型更新的大小。

其中 \(\alpha>1\) 是根据模型参数定的常数。这里相比post-norm提升了恒等分支的权重,使训练更容易进行。
另外,还用了一个 \(\beta\) 参数,把 \(G_{l}\) 中的模型参数进行了缩小,以此来稳定模型的训练。
实验结果上,deepnorm结合了pre-norm的容易训练,和post-norm的收敛效果好的特点,能够把百层、浅层的模型训到比较好的效果。
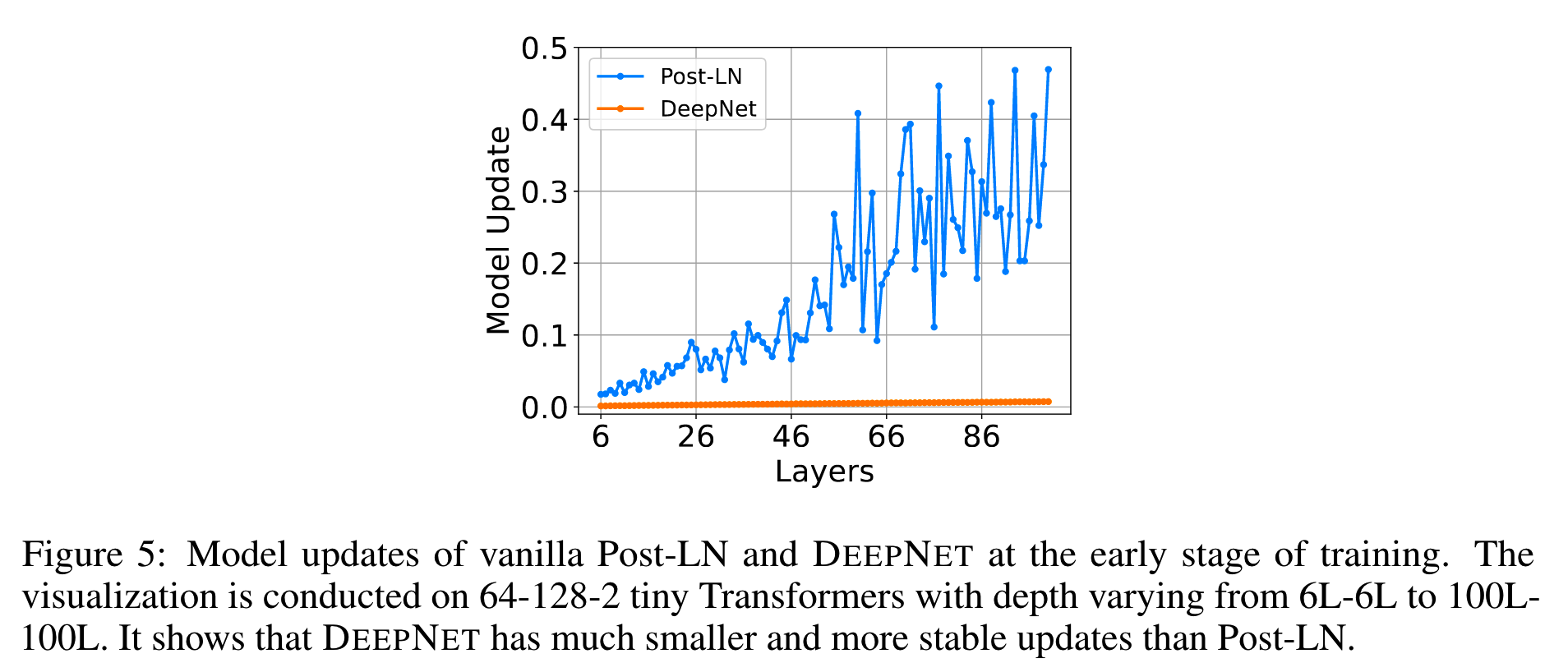
参数过程相比post-norm稳定了很多。
Realformer--residual attention
post-norm和pre-norm实际上改变的是模型残差分支和恒等分支怎么排布的问题,而《RealFormer: Transformer Likes Residual Attention》则提出了另外一种做法
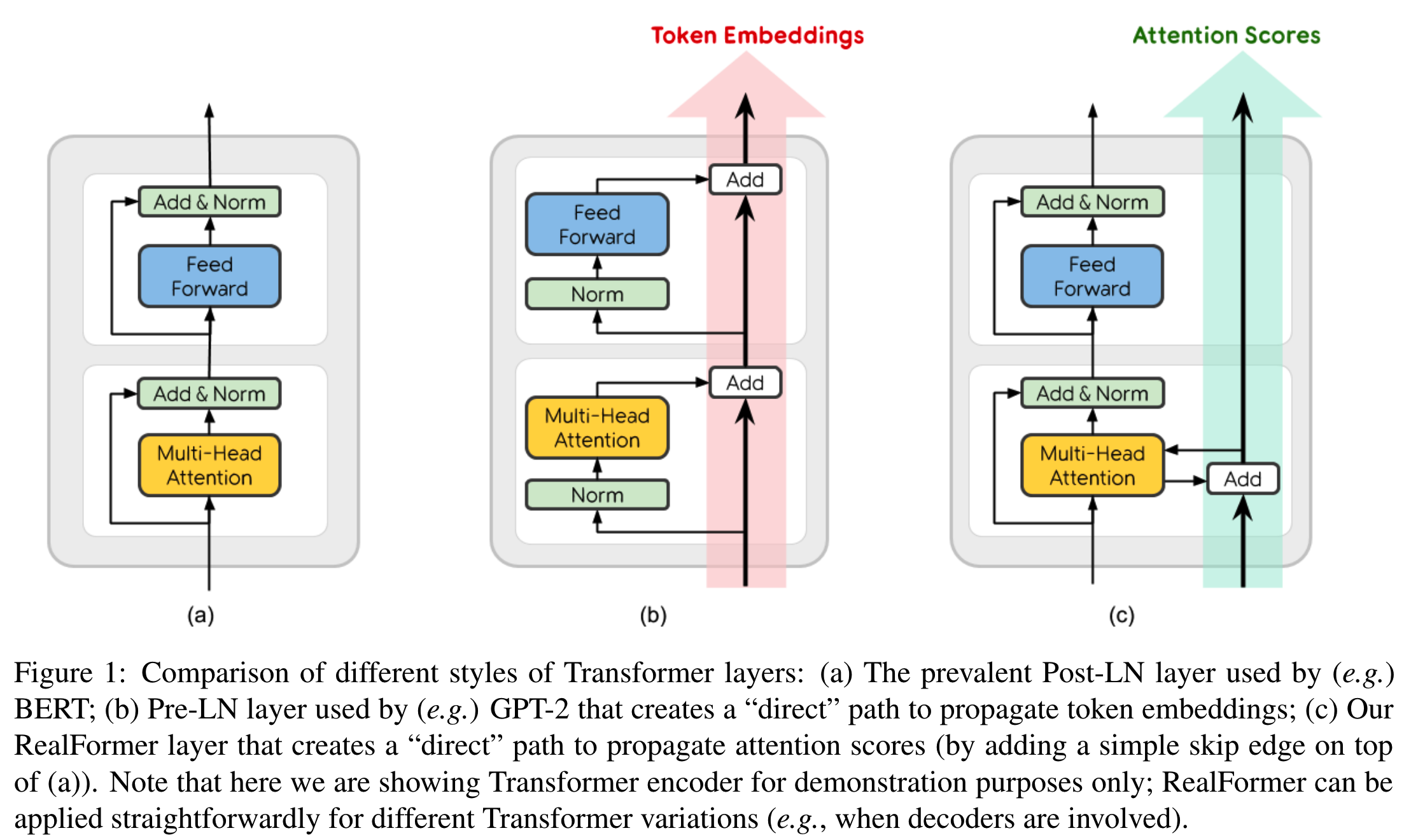
RealFormer的核心是在其标准Transformer编码器的每一层中引入了残差连接。这些残差连接将前一层的原始注意力分数(即在应用Softmax之前的分数)与当前层计算出的注意力分数相结合。这样做的结果是,当前层的注意力分数在计算时会考虑到前一层的信息。
每个多头注意力模块都会接收来自前一层的残差注意力分数作为额外输入。这意味着每个注意力头不仅考虑了当前层内的输入序列,而且还直接利用了前一层的注意力信息。
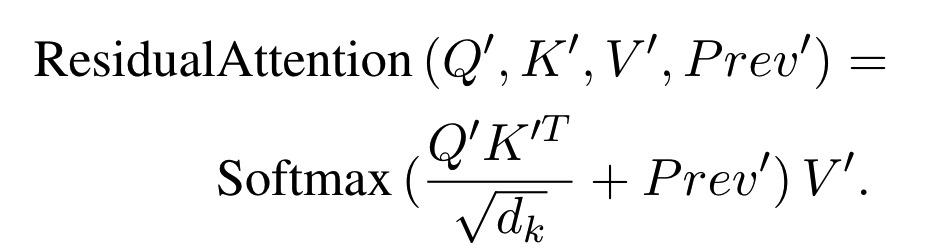
其中 \(Prev'\) 是来自上一层softmax之前的权重矩阵(多头注意力的话,则是对应的头的值),而 \(\frac{Q^{\prime}K^{\prime T}}{\sqrt{d_k}}+Prev'\) 则是传给下一层的attention的。
小结
本篇粗略梳理了一下关于normalization,batchnorm,以及layernorm在transformer的一些使用情况。
目前主流的大模型使用的是rmsnorm + prenorm,也有使用其他变体的。
关于normalization,依然留有一些探索空间。
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

往期文章
稀疏注意力计算:sliding window attention
Reference
【1】https://www.zhihu.com/question/487766088
【2】Towards Stabilizing Batch Statistics in Backward Propagation of
Batch Normalization https://arxiv.org/abs/2001.06838
【3】Transformer中的归一化(一):什么是归一化&为什么要归一化
https://zhuanlan.zhihu.com/p/476102712
【4】Batch Normalization: Accelerating Deep Network Training by Reducing
Internal Covariate Shift https://arxiv.org/abs/1502.03167
【5】How Does Batch Normalization Help Optimization?
https://arxiv.org/abs/1805.11604
【6】Batch Normalization: Accelerating Deep Network
https://zhuanlan.zhihu.com/p/340856414
【7】Layer Normalization https://arxiv.org/abs/1607.06450
【8】详解深度学习中的Normalization,BN/LN/WN
https://zhuanlan.zhihu.com/p/33173246
【9】Transformer中的归一化(四):BatchNormalization的原理、作用和实现
https://zhuanlan.zhihu.com/p/481277619
【10】Layer Normalization https://arxiv.org/abs/1607.06450
【11】PowerNorm: Rethinking Batch Normalization in Transformers
https://arxiv.org/abs/2003.07845
【12】Root Mean Square Layer Normalization
https://arxiv.org/abs/1910.07467
【13】On Layer Normalization in the Transformer Architecture
https://arxiv.org/abs/2002.04745
【14】为什么Pre Norm的效果不如Post Norm?
https://spaces.ac.cn/archives/9009
【15】Understanding the Difficulty of Training Transformers
https://arxiv.org/abs/2004.08249
【16】RealFormer: Transformer Likes Residual Attention
https://arxiv.org/abs/2012.11747
【17】DeepNet: Scaling Transformers to 1,000 Layers
https://arxiv.org/abs/2203.00555