理解LLM位置编码:RoPE
最近在做LLM窗口外推的相关工作,因此刚好也回顾一下目前最流行的位置编码RoPE。
关于RoPE
RoPE(Rotary Position Embedding),是苏剑林大神在2021年就提出的一种Transformer模型的位置编码。RoPE是一种可以以绝对位置编码形式实现的相对位置编码,兼顾了模型性能和效率。
2023年上半年的时候,大模型位置编码尚有Alibi和RoPE在相互比拼,而到了2023年下半年,及今2024年,新开源出来的模型,大部分都是使用RoPE了。当然Alibi也有其优势,这个在讲Alibi的时候来说。
苏神在他的个人网站科学空间中对RoPE有相关文章进行了介绍,本篇是在这个基础上,对RoPE进行理解(公式和符号上也会沿用苏神的写法)。
以绝对位置编码的方式实现相对位置编码
前面提到,RoPE是一种一绝对位置编码的方式实现的相对位置编码,那么这么做能带来什么收益?
先说原因:
在文本长度不长的情况下(比如Bert时代基本都是256/512token的长度),相对位置编码和绝对位置编码在使用效果上可以说没有显著差别。
如果要处理更大长度的输入输出,使用绝对位置编码就需要把训练数据也加长到推理所需长度,否则对于没训练过的长度(训练时没见过的位置编码),效果多少会打些折扣。
而使用相对位置编码则更容易外推,毕竟token-2和token-1的距离,与token-10002和token-10001的距离是一样的,也因此可以缓解对巨量长文本数据的需求。
但是传统相对位置编码的实现相对复杂,有些也会有计算效率低的问题。由于修改了self-attention的计算方式,也比较难推广到线性注意力计算法模型中。
总结来说,就是绝对位置编码好实现,效率高,适用线性注意力,而相对位置编码易外推,因此就有了对“绝对位置编码的方式实现相对位置编码”的追求,去把二者的优点结合起来。
下面简单回顾一下绝对位置编码和相对位置编码。
(对位置编码比较熟悉的朋友可以直接跳到第3节。)
绝对位置编码
先回顾一下带绝对位置编码的self-attention。
\[\left.\left\{\begin{array}{l}q_\mathrm{i}=(x_\mathrm{i}+p_\mathrm{i})W_\mathrm{Q}\\k_\mathrm{j}=(x_\mathrm{j}+p_\mathrm{j})W_\mathrm{K}\\\nu_\mathrm{j}=(x_\mathrm{j}+p_\mathrm{j})W_\mathrm{V}\\\mathrm{a_\mathrm{i,j}}=\mathrm{softmax}\left(q_\mathrm{i}k_\mathrm{j}^\top\right)\\o_\mathrm{i}=\sum_\mathrm{j}a_\mathrm{i,j}\nu_\mathrm{j}\end{array}\right.\right.\tag{1}\]
\(x_i\) 和 \(x_j\) 分别是位置 \(i\) 和 \(j\) 的输入,\(p\) 是对应位置的位置编码向量。
这里的位置编码\(p\)可以是三角函数式,或者直接训练式。但是无论是哪种,其实现方式都很简单,就是在输入端把词向量 \(x\) 和位置向量 \(p\) 相加即可,相比attention中的softmax计算,element-wise addition操作的计算量非常小,是可以忽略不计的。
大部分绝对位置编码使用的是这样向量相加的形式,即加性编码,也有一些用乘性编码的工作,把 \(x + p\) 变成 \(x * p\) 这样,效果上也是大差不差。
相对位置编码
在绝对位置编码中,可以在输入阶段就把 \(x\) 和 \(p\) 直接相加,是因为这里把位置信息当做是这个位置的词的固有特征。
比如“我”这个词放在位置1时,形成一个 \(e_1 = x_我 + p_1\) 这么一个向量来代表【“我”在位置1】这一个情况;而当同样的词“我”放在位置8时,形成了另一个向量 \(e_8 = x_我 + p_8\) 。两个向量 \(e_1\) 和 \(e_8\) 虽然包含同一个词,但是对于模型来说,这两个输入是不同的(因为每个数值都包含了位置向量),词向量和位置向量耦合在一起共同构成了一个完整的输入。
直观来说,比如词表大小是1万,模型训练窗口最大长度是512,那么对于模型来说,实际上要区分的输入是1万×512=512万个。看起来虽然不少,但是在海量的数据和训练量下,这也不算什么事儿,模型确实能handle。
扯远了,现在回来看一下相对位置编码。把公式(1)中的 \(q_{i}k_{j}^{T}\)展开来
\[\begin{align*}q_ik_j^\top&=\left(x_i+p_i\right)W_\mathbb{Q}W_K^\top\left(x_j+p_j\right)^\top\\&=\left(x_iW_\mathbb{Q}+{\color{red}p_iW_\mathbb{Q}}\right)\left(W_K^\top x_j^\top+{\color{red}W_K^\top p_j^\top}\right)\end{align*}\tag{2}\]
和位置相关的有 \(p_iW_\mathbb{Q}\) 和 \(W_K^\top p_j^\top\) 两项。
Google式
在最早引入相对位置编码的Google的论文《Self-Attention with Relative Position Representations》中,把第一项 \(p_iW_\mathbb{Q}\) 去掉了(因为要搞相对位置编码,只要能把相对位置信息加到其中一项输入就可以了,这里加在了位置 \(j\)),把第二项 \(W_K^\top p_j^\top\) 改成和位置 \(i\)、\(j\) 都相关的位置向量 \(R_{ij}^K\),于是在这个使用相对位置编码的attention计算中,不再是直接计算input projection的内积来获取权重,而变成
\[ \mathrm{a_{ij}=softmax}\left(x_{i}W_{\mathbb{Q}}\left(x_{j}W_{\mathbb{K}}+R_{\mathbf{i,j}}^{\mathbf{K}}\right)^{\top}\right)\tag{3} \]
\(R_{ij}^K\) 是什么呢?可以是可训练式的向量,也可以是类似三角函数式的,在这个基础上增加了一个clip操作。
\[ R_{\mathrm{i,j}}^\mathrm{K}=p_\mathrm{K}\left[\mathrm{clip(i-j,p_{min},p_{max})}\right] \]
其中 \(p_\mathrm{K}\) 就是可训练的向量或者三角函数向量。
为什么要增加一个clip操作?因为直观上,一个词对其左右附近的其他词的位置关系理应更加敏感,比如“我请你吃饭”中,“吃饭”这个词需要以高分辨率明确区分出前面三个词“我”、“请”、“你”的位置,以免理解成了“你请我吃饭”;而随着距离越来越远,这种高分辨率的需求也就越来越低,十万个token之前的内容顺序对于当前token来说,影响比较小了,在位置向量上可以一视同仁。另外这也是方便了位置信息的外推,比如我们可以只训练256个相对位置编码信息,而在应用是可以外推到>256的长度。
本来到这里就可以了,相对位置信息已经加入了,但是Google除了在input端增加了相对位置信息,在输出端也增加了相对位置信息。本来输出端的计算是
\[\begin{align*} o_\mathrm{i}&=\sum_\mathrm{j}a_\mathrm{i,j}\nu_\mathrm{j}\\ &=\sum_{\mathrm{j}}\mathrm{a_{i,j}}(x_{j} + p_{j})W_{\mathrm{V}}\\ &=\sum_{\mathrm{j}}\mathrm{a_{i,j}}(x_{j}W_{\mathrm{V}} + {\color{red}p_{j}W_{\mathrm{V}}})\\ \end{align*}\tag{4}\]
Google的方法把 \(p_{j}W_{\mathrm{V}}\) 也改成了包含相对位置信息的向量
\[\begin{align*} o_{\mathrm{i}}=\sum_{\mathrm{j}}\mathrm{a_{i,j}}\left(x_{j}W_{\mathrm{V}}+R_{\mathrm{i,j}}^{\mathrm{V}}\right)\tag{5} \end{align*}\]
\(R_{\mathrm{i,j}}^{\mathrm{V}}\) 和 \(R_{ij}^K\) 相似,都是一个相对位置向量 + clip操作。
XLNET式
XLNET也使用了相对位置编码,思路类似Google,只是具体的操作不同。
在公式(2)的基础上继续展开
\[\begin{align*} q_ik_j^T &= \left(x_iW_\mathbb{Q}+{p_iW_\mathbb{Q}}\right)\left(W_K^\top x_j^\top+{W_K^\top p_j^\top}\right)\\ &= x_iW_\mathbb{Q}W_\mathbb{K}^Tx_j^T +x_iW_\mathbb{Q}W_\mathbb{K}^T{\color{red}p_j^T} +{\color{red}p_i}W_\mathbb{Q}W_\mathbb{K}^T{x_j^T} +{\color{red}p_i}W_\mathbb{Q}W_\mathbb{K}^T{\color{red}p_j^T}\\ \end{align*}\tag{6} \]
把绝对位置相关的几个参数改成相对位置相关的参数,变成:
\[ \mathrm{a_{ij}=softmax}\left (x_iW_\mathrm{Q}W_\mathrm{K}^\top x_\mathrm{j}^\top +x_iW_\mathrm{Q}W_\mathrm{K}^\top {\color{red}R_\mathrm{i-j}^\top} +{\color{red}u}W_\mathrm{Q}W_\mathrm{K}^\top x_\mathrm{j}^\top +{\color{red}\nu} W_\mathrm{Q}W_\mathrm{K}^\top{\color{red}R_\mathrm{i-j}^\top}\right) \tag{7} \]
把 \(p_i\) 变成了两个可训练的向量 \(u\) 和 \(\nu\) ,把 \(p_j\) 变成相对位置向量 \(R_{i-j}^\top\) 。
实际实现上可以把 \(u\) 和 \(\nu\) 后面跟着的矩阵省掉了,去掉这个线性变化不影响 \(u\) 和 \(\nu\) 的训练,变成
\[ x_iW_\mathrm{Q}W_\mathrm{K}^\top x_\mathrm{j}^\top +x_iW_\mathrm{Q}W_\mathrm{K}^\top {\color{red}R_\mathrm{i-j}^\top} +{\color{red}u}W_\mathrm{K}^\top x_\mathrm{j}^\top +{\color{red}\nu} W_\mathrm{K}^\top{\color{red}R_\mathrm{i-j}^\top} \tag{8} \]
此外,XLNET只对输入端做了处理,输出端则直接把位置相关的计算去掉了,即
\[\begin{align*} o_\mathrm{i} &=\sum_{\mathrm{j}}\mathrm{a_{i,j}}x_{j}W_{\mathrm{V}}\\ \end{align*}\tag{9}\]
可以看到,Google式和XLNET式的相对位置编码在权重 \(\mathrm{a_{i,j}}\) 的计算上都变得比较复杂了(相对绝对位置编码而言),并且到这里可以看到,获取相对位置信息的思路其实就是想办法把原来公式(2)中的绝对位置向量替换成和位置 \(i\) 、 \(j\) 都相关的向量。很多其他变体其实都大差不差,基本就是在怎么加入相对位置向量、怎么clip上下功夫。
当然,也有简单一点的实现,比如T5的方法。
T5式
公式(6)中展开了内积计算,一共有四项,第一项完全没有位置信息,只和词向量本身有关,第二三项分别包含了位置 \(i\) 和位置 \(j\) 的信息,而第四项只和位置相关,和词向量本身是什么内容无关。也就是说,位置相关的信息都是在后面三项引入的,那简单点,直接把后面三项替换成一个位置向量:
\[ \mathrm{a_{ij}=softmax}\left (x_iW_\mathrm{Q}W_\mathrm{K}^\top x_\mathrm{j}^\top + \beta_{i,j}\right) \tag{10} \]
(从最早提出,到XLNET,以及DeBerta,T5等,可以看到相对位置编码的实现有一个简化的趋势,而效果也越来越好,正所谓大道至简,有时候有用的东西未必需要很复杂)
对比
看来相对位置编码确实比较复杂,说个大概需要这么多篇幅;并且相对绝对位置编码,也没有那么直接明了,需要对attention计算做一些改造。
公式(1)的绝对位置编码中,可以看到在进softmax操作前需要做3次矩阵加法,3次矩阵乘法
从公式(8)可以看到,共有4组矩阵计算要做,每组要做3次矩阵乘法,相对会比较复杂。公式(3)也有类似的情况。当然同时也有一些针对相对位置编码的高效计算被提出,这些就需要针对不同的计算方案来优化了。
总之在实现方式上和计算效率上,绝对位置编码具有一些优势。
而在输入输出窗口外推方面,相对位置编码有着天然的优势。
另外,绝对位置编码保持self-attention的经典形式,使得应用面更广,如可以使用到linear attention方案中去,这个以后再展开讲(又挖了个坑)。
RoPE的设计思路
保持attention计算形式
回顾完经典的绝对位置编码和相对位置编码,回到RoPE上来。
先说设计思路:
首先我们想要保持经典self-attention的计算方式,即公式(1)中的形式,输入端 = 内积 + softmax,至于输出端则保持完全不变。softmax我们不去动,那这里留给我们操作的就是内积。
也就说,现在问题是,我们怎么在只做内积的情况下,把内积结果变成只和相对位置有关,而和绝对位置无关的结果。写成公式就是
\[ \langle f_q(\boldsymbol{q}_m,m),f_k(\boldsymbol{k}_n,n)\rangle=g(\boldsymbol{q}_m,\boldsymbol{k}_n,m-n) \tag{11} \]
其中 \(q_m\) 是在位置 \(m\) 的query向量,\(k_n\) 是在位置 \(n\) 的key向量,\(f_q\) 和 \(f_k\) 是分别针对这query和key向量的操作函数。
我们的任务就是要找到一组 \(f_q\) 、 \(f_k\) 和 \(g\) ,使得公式(11)恒成立。
当然理论上这里是存在无数多组答案的,那么RoPE怎么找到一组好实现的组合呢?
借用复数寻找组合
式(11)中, \(g\) 的结果是一个标量,我们需要一个能连接向量内积和标量的桥梁,这个桥梁就是复数。
这里先回顾一下复数的知识。任意复数都可以表示成复平面的一个2维向量
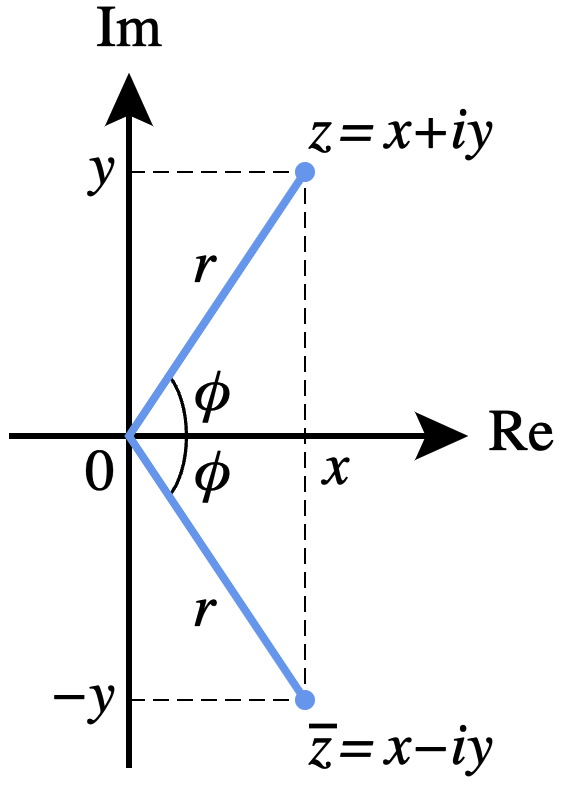
现在考虑query和key向量都是2维的情况,那么可以代入复数的操作
(先把 hidden size = 2 的情况推理清楚,后续再推广到更高维的情况)
那么在2维复数平面上有什么操作可以满足公式(11)的要求呢?Roformer论文中提出的是这组:
\[ \begin{aligned} f_q(\boldsymbol{q}_m,m)&=\boldsymbol{q}_me^{im\theta}=\left(\boldsymbol{W}_q\boldsymbol{x}_m\right)e^{im\theta} \\ f_k(\boldsymbol{k}_n,n)&=\boldsymbol{k}_ne^{in\theta}=(\boldsymbol{W}_k\boldsymbol{x}_n)e^{in\theta} \\ g(\boldsymbol{q}_m,\boldsymbol{k}_n,m-n)&=\mathrm{Re}\left[\boldsymbol{q}_m\boldsymbol{k}_n^*e^{i(m-n)\theta}\right] =\mathrm{Re}\left[(\boldsymbol{W}_q\boldsymbol{x}_m)(\boldsymbol{W}_k\boldsymbol{x}_n)^*e^{i(m-n)\theta}\right]\\ \end{aligned} \\ \tag{12} \]
其中 \(\boldsymbol{k}_n^*\) 是 \(\boldsymbol{k}_n\) 的共轭复数。
(如果暂时理解不了是怎么想出这个组合来满足要求的的,先把它放一边,毕竟数学就是这么神奇)
共轭复数是这样的关系
\[ \begin{gathered} z=a+ib \\ z^*=a-ib \end{gathered} \tag{13} \]
先证明一下这个组合的正确性,是不是真的满足公式(11)。
(也可以先跳过证明,选择先相信这个组合)
回顾一下欧拉公式
\[ e^{ix}=\cos x+i\sin x \tag{14} \]
因为现在我们讨论的是2维的情况,那2维向量 \(q_m\) 可以用一个复数来表示
\[ q_m = q_m^{(1)} + iq_m^{(2)} \tag{15} \]
那从复数角度来看,就有
\[ \begin{aligned} f_q(\boldsymbol{q}_m,m) &= \boldsymbol{q}_me^{im\theta} \\ &= (q_m^{(1)} + iq_m^{(2)})(\cos (m\theta)+i\sin (m\theta)) \\ &= (q_m^{(1)}cos(m\theta)-q_m^{(2)}\sin(m\theta))+i(q_m^{(1)}\sin(m\theta) + q_m^{(2)}\cos(m\theta)) \end{aligned} \tag{16} \]
式(16)的结果也是一个复数,那也可以用复平面上的一个向量来表示:
\[ f_q(\boldsymbol{q}_m,m) = \left.\left[\begin{matrix}{q_m^{(1)}cos(m\theta)-q_m^{(2)}\sin(m\theta)}\\{q_m^{(1)}\sin(m\theta) + q_m^{(2)}\cos(m\theta)}\end{matrix}\right.\right]^\top \tag{17} \]
(这里沿用式(1)中,默认向量为行向量的设定,所有有个transpose,实际上是行向量还是列向量都没关系,只是推算的时候写法问题)
类似地,有
\[ \begin{aligned} f_k(\boldsymbol{k}_n,n) &= (k_n^{(1)}cos(n\theta)-k_n^{(2)}\sin(n\theta))+i(k_n^{(1)}\sin(n\theta) + k_n^{(2)}\cos(n\theta)) \end{aligned} \tag{18} \]
和
\[ f_k(\boldsymbol{k}_n,n) = \left.\left[\begin{matrix}{k_n^{(1)}cos(n\theta)-k_n^{(2)}\sin(n\theta)}\\{k_n^{(1)}\sin(n\theta) + k_n^{(2)}\cos(n\theta)}\end{matrix}\right.\right]^\top \tag{19} \]
则有
\[
\begin{aligned}
&\langle
f_q(\boldsymbol{q}_m,m),f_k(\boldsymbol{k}_n,n)\rangle\\=&(q_m^{(1)}cos(m\theta)-q_m^{(2)}\sin(m\theta))(k_n^{(1)}cos(n\theta)-k_n^{(2)}\sin(n\theta))
\\&+ (q_m^{(1)}\sin(m\theta) +
q_m^{(2)}\cos(m\theta))(k_n^{(1)}\sin(n\theta) +
k_n^{(2)}\cos(n\theta))\\
=&q_m^{(1)}k_n^{(1)}\left(\cos(m\theta)\cos(n\theta)+\sin(m\theta)\sin(n\theta)\right)
\\
&+q_m^{(1)}k_n^{(2)}\left(-\cos(m\theta)\sin(n\theta)+\sin(m\theta)\cos(n\theta)\right)
\\
&+q_m^{(2)}k_n^{(1)}(-\sin(m\theta)\cos(n\theta)+\cos(m\theta)\sin(n\theta))
\\
&+q_m^{(2)}k_n^{(2)}(\sin(m\theta)\sin(n\theta)+\cos(m\theta)\cos(n\theta))
\\
=&q_m^{(1)}k_n^{(1)}\cos((m-n)\theta)+q_m^{(1)}k_n^{(2)}\sin((m-n)\theta)
\\
&-\left.q_m^{(2)}k_n^{(1)}\right.\sin((m-n)\theta)
+q_m^{(2)}k_n^{(2)}\cos((m-n)\theta)\\
= &(q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})\cos((m - n)\theta) +
(q_m^{(1)}k_n^2 - q_m^{(2)}k_n^{(1)})\sin((m-n)\theta)
\end{aligned}
\tag{20}
\]
用了三角函数和差公式 \[ \sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\\ {\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta} \]
再看 \(g\)
\[ \begin{aligned} &g(\boldsymbol{q}_m,\boldsymbol{k}_n,m-n)\\ = &\mathrm{Re}\left[\boldsymbol{q}_m\boldsymbol{k}_n^*e^{i(m-n)\theta}\right] \\ = &\mathrm{Re}\left[[(q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)}) - i(q_m^{(1)}k_n^2 - q_m^{(2)}k_n^{(1)})](\cos((m - n)\theta) + i\sin((m-n)\theta))\right] \\ = &(q_m^{(1)}k_n^{(1)} + q_m^{(2)}k_n^{(2)})\cos((m - n)\theta) + (q_m^{(1)}k_n^2 - q_m^{(2)}k_n^{(1)})\sin((m-n)\theta)\\ = &\langle f_q(\boldsymbol{q}_m,m),f_k(\boldsymbol{k}_n,n)\rangle \end{aligned} \tag{21} \]
证毕。
“旋转”位置编码
发现式(17)可以写成这样
\[ f_q(\boldsymbol{q}_m,m)^\top = \left.\left[\begin{matrix}{\cos(m\theta)}&{-\sin(m\theta)}\\{\sin(m\theta)}&{\cos(m\theta)}\end{matrix}\right.\right] {\left.\left[\begin{matrix}{q_m^{(1)}}\\{q_m^{(2)}}\end{matrix}\right.\right]} \tag{22} \]
同样地
\[ f_k(\boldsymbol{k}_n,n)^\top = \left.\left[\begin{matrix}{\cos(n\theta)}&{-\sin(n\theta)}\\{\sin(n\theta)}&{\cos(n\theta)}\end{matrix}\right.\right] {\left.\left[\begin{matrix}{k_n^{(1)}}\\{k_n^{(2)}}\end{matrix}\right.\right]} \tag{23} \]
如果从向量视角来看,则有
\[ \begin{aligned} &\langle f_q(\boldsymbol{q}_m,m),f_k(\boldsymbol{k}_n,n)\rangle\\ =&{\left.\left[\begin{matrix}{q_m^{(1)}}&{q_m^{(2)}}\end{matrix}\right.\right]} \left.\left[\begin{matrix}{\cos(m\theta)}&{\sin(m\theta)}\\{-\sin(m\theta)}&{\cos(m\theta)}\end{matrix}\right.\right] \left.\left[\begin{matrix}{\cos(n\theta)}&{-\sin(n\theta)}\\{\sin(n\theta)}&{\cos(n\theta)}\end{matrix}\right.\right] {\left.\left[\begin{matrix}{k_n^{(1)}}\\{k_n^{(2)}}\end{matrix}\right.\right]}\\ =&{\left.\left[\begin{matrix}{q_m^{(1)}}&{q_m^{(2)}}\end{matrix}\right.\right]}\left.\left[\begin{matrix}{\cos(m\theta)\cos(n\theta) + \sin(m\theta)\sin(n\theta)}& {-\cos(m\theta)\sin(n\theta) + \sin(m\theta)\cos(n\theta)}\\ {-\cos(n\theta)\sin(m\theta) + \cos(m\theta)\sin(n\theta)}& {\sin(m\theta)\sin(n\theta) + \cos(m\theta)\cos(n\theta)} \end{matrix}\right.\right] {\left.\left[\begin{matrix}{k_n^{(1)}}\\{k_n^{(2)}}\end{matrix}\right.\right]}\\ =&{\left.\left[\begin{matrix}{q_m^{(1)}}&{q_m^{(2)}}\end{matrix}\right.\right]} \left.\left[\begin{matrix}{\cos((m-n)\theta)}&{\sin((m-n)\theta)}\\{-\sin((m-n)\theta)}&{\cos((m-n)\theta)}\end{matrix}\right.\right] {\left.\left[\begin{matrix}{k_n^{(1)}}\\{k_n^{(2)}}\end{matrix}\right.\right]} \end{aligned} \tag{24} \]
看式(22)和(23),可以看到等号右边都有
\[ \left.\left[\begin{matrix}{\cos(n\theta)}&{-\sin(n\theta)}\\{\sin(n\theta)}&{\cos(n\theta)}\end{matrix}\right.\right] \]
这正是一个二维平面的旋转矩阵。 \(f_q\) 、 \(f_k\) 的操作相当于对输入向量进行了一次不改变大小,只改变方向的旋转。
这也是为什么叫做“旋转”位置编码。
从2维推广到高维
我们现在已经确认,对于2维的情况,经过 \(f_q\) 、 \(f_k\) 和 \(g\) 这么一波操作,能够满足式(11)的要求,但是实际上怎么在高维模型里实现呢?
答案是把高维输入拆分成两个两个一组(这要求输入是偶数维,目前的模型也都是偶数维,所以没问题),则高维的“旋转”矩阵有多个小旋转矩阵组成
\[ \boldsymbol{R}_{\Theta,m}^d=\begin{pmatrix}\cos m\theta_0&-\sin m\theta_0&0&0&\cdots&0&0\\\sin m\theta_0&\cos m\theta_0&0&0&\cdots&0&0\\0&0&\cos m\theta_1&-\sin m\theta_1&\cdots&0&0\\0&0&\sin m\theta_1&\cos m\theta_1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\\0&0&0&0&\cdots&\sin m\theta_{d/2-1}&\cos n\theta_{d/2-1}\end{pmatrix} \tag{25} \]
\(d\) 是的输入向量的维度,由于是两个两个一组,所以一共有 \(d/2\) 组小旋转矩阵,这 \(d/2\) 组矩阵为了区分,设计使用了不同的 \(\theta\)
\[ \Theta=\left\{\theta_i=10000^{-2(i-1)/d},i\in[1,2,\ldots,d/2]\right\} \tag{26} \]
那么在实际操作的时候,给位置 \(m\) 和位置 \(n\) 的输入向量分别乘以 \(R_m\) 和 \(R_n\),再进行self-attention,就能获得仅使用相对位置信息编码的效果。
另外 \(\theta\) 是怎么来的呢?这里是参考了Google最初在《Attention is All You Need》中提出的,这里就先不展开了,可以看看论文原文。
高效率实现
式(25)中的矩阵在高维的情况下很稀疏,直接使用这么个矩阵来计算效率并不高,可以使用一个这样的高效率实现方式
\[ \boldsymbol{R}_{ m}\boldsymbol{q}=\begin{pmatrix}q_0\\q_1\\q_2\\q_3\\q_4\\\vdots\\q_{d-2}\\q_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{pmatrix} +\begin{pmatrix}-q_1\\q_0\\-q_3\\\vdots\\-q_{d-1}\\q_{d-2}\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0\\\sin m\theta_0\\\sin m\theta_1\\\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{pmatrix} \tag{27} \]
只需进行两组element-wise乘法即可。形式上看起来是类似乘性绝对位置编码的做法。
另外,看LLAMA中的实现,可以看到旋转位置编码是在每一个decoder层的输入都加了的。每次都强化一次位置信息,也有助于模型更好识别不同距离的内容。
远程衰减的特性
至此,旋转位置编码已经完备,具备了计算高效,实现容易,便于外推,适用于线性注意力的特性。实际上它还具备另一项优点:有远程衰减的特性。
直观看起来远程衰减很符合直觉,毕竟注意力机制随着距离的衰减而降低,这个机制和人类也很像。
回顾训练式的绝对位置编码,由于每个位置的位置向量是模型在训练中自我学习的,所以并不保证能具备这样的特性。而这个 \(\theta\) 的选择沿用了三角函数式编码的做法,就使得整体具有远程衰减的特性。
证明过程这里就偷偷懒略过了,具体可以看Roformer的论文或者苏神的博客。
当 \(d = 128\) 时,画出来的图像如下
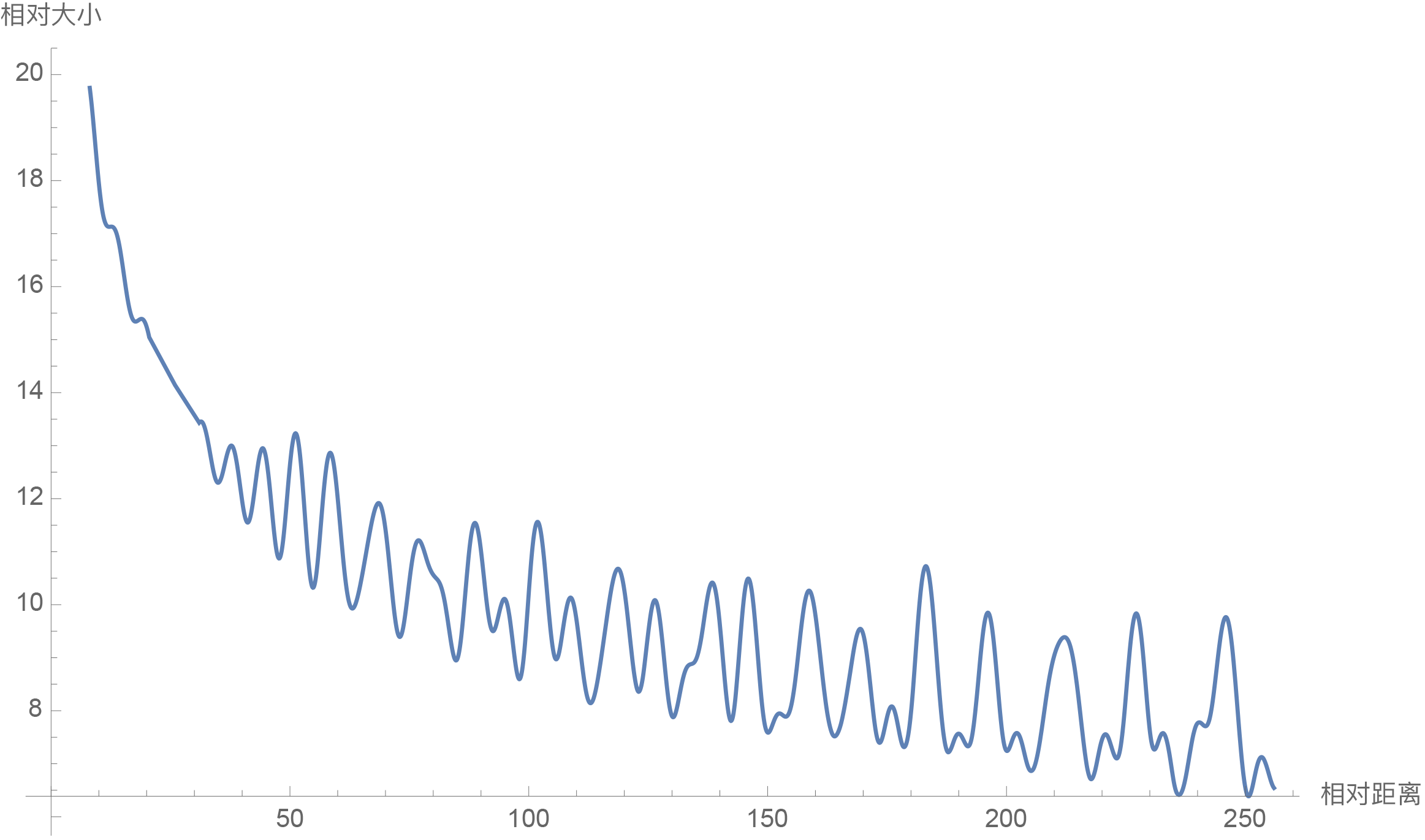
小结
总之,RoPE在设计和实现上还是挺巧妙的,性质上也很有很多优势,所以被广泛应用到transformer模型中去了。
Reference
【1】让研究人员绞尽脑汁的Transformer位置编码,https://spaces.ac.cn/archives/8130
【2】Transformer升级之路:2、博采众长的旋转式位置编码,https://spaces.ac.cn/archives/8265
【3】RoFormer: Enhanced Transformer with Rotary Position Embedding
https://arxiv.org/abs/2104.09864
【4】十分钟读懂旋转编码(RoPE)
https://zhuanlan.zhihu.com/p/647109286
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight
