大模型偏好对齐-ODPO
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
前面对DPO的思路做了整理:大模型偏好对齐-DPO。
DPO把RLHF的两阶段训练,变成了一阶段训练,降低了训练成本。而ODPO(DPO with an offset)在DPO的基础上做了一点改进,在几个下游任务的实验中,获得了比DPO更好的效果。
背景
直接使用指令微调,是让模型学会处理下游任务的一个快速有效的方法。
但是指令微调的优化目标是maximize the response log-likelihood,这和“生成人类所偏好的高质量内容”的目标之间存在gap,不完全对齐。
这个misalignment部分是因为maximum likelihood的目标无法区分数据里“大错”(比如幻觉)和“小错”(比如标点符号不恰当)。
Training with the maximum likelihood objective makes the model assign nonzero probability mass to all responses in SFT dataset, even those of lower quality.
因此有RLHF的方法来解决这个问题。RL通过人类偏好数据训练一个reward模型,并用reward模型来指导策略模型。
而reward的modeling有两种,pointwise reward和pairwise preference。
pointwise reward一般用于reward有比较确定定义且简单的场景,比如情感分类,我们可以定义positive的情感的reward为1,negative的reward为0。类似的还有toxicity等。这些类别一般也有很多现成的打分模型/classifier可以使用。
pairwise preference一般用于比较复杂的任务,比如文本摘要和对话生成。这类任务难以直接基于单个答案来打分,而需要通过对比才能知道哪个更好。
但RLHF成本比较高,因此DPO对训练过程进行了简化。
Bradley–Terry model的局限
DPO的损失如下
\[\begin{aligned} \mathcal{L}^{\mathrm{DPO}}(\boldsymbol{\theta})& =-\mathbb{E}_{(\boldsymbol{x},\boldsymbol{y}_w,\boldsymbol{y}_l)\sim\mathcal{D}_{\text{HF}}}\left[\log\sigma\Big(\beta\log\frac{\pi_{\boldsymbol{\theta}}(\boldsymbol{y}_w\mid\boldsymbol{x})}{\pi_{\text{SFT}}(\boldsymbol{y}_w\mid\boldsymbol{x})}-\beta\log\frac{\pi_{\boldsymbol{\theta}}(\boldsymbol{y}_l\mid\boldsymbol{x})}{\pi_{\text{SFT}}(\boldsymbol{y}_l\mid\boldsymbol{x})}\Big)\right] \\ &=-\underset{(\boldsymbol{x},\boldsymbol{y}_w,\boldsymbol{y}_l)\thicksim\mathcal{D}_{\mathrm{HF}}}{\operatorname*{\mathbb{E}}}\left[\log\sigma\left(\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_w)-\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_l)\right)\right] \end{aligned}\]
其中
\[\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y})=\beta\log\frac{\pi_{\boldsymbol{\theta}}(\boldsymbol{y}|\boldsymbol{x})}{\pi_{\mathrm{SFT}}(\boldsymbol{y}|\boldsymbol{x})}\]
是estimated reward。
这个DPO损失的形式背后用到了Bradley–Terry model对偏好进行建模。而Bradley–Terry model只给出了一个response比另一个response好的概率,而没有告诉我们好的程度。
而实际上我们很多偏好对比数据都提供了具体的分数,而不仅仅是排序信息。有这些具体分数我们就可以知道两条response之间是差一点点,还是差很多。
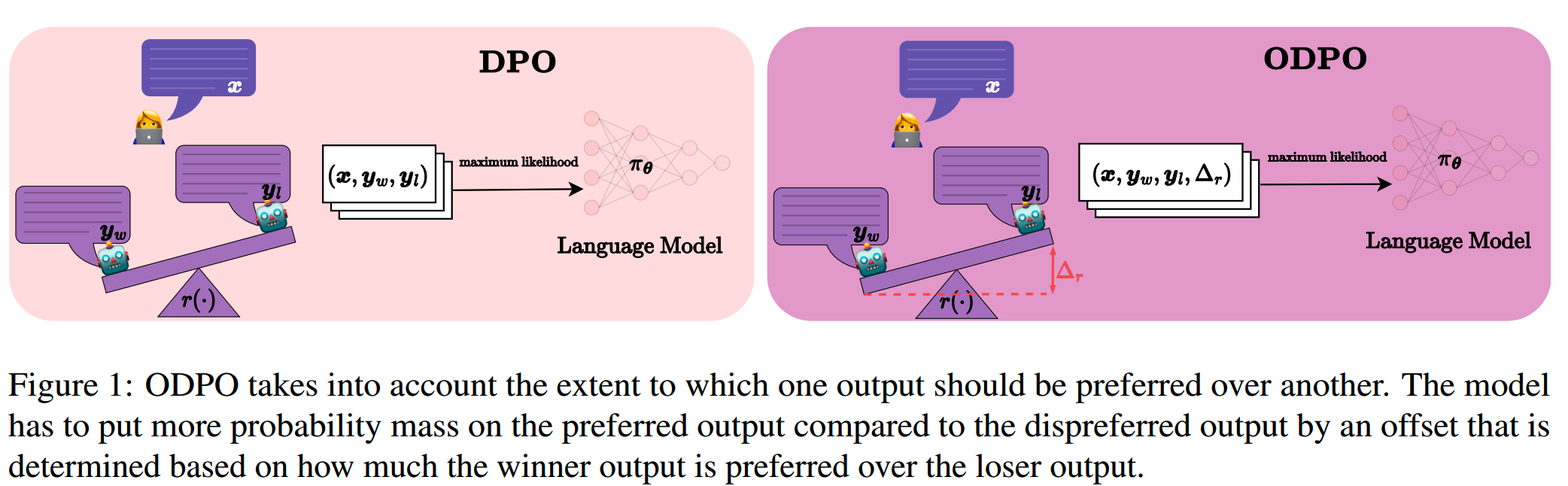
那么把这个差距的信息引入到偏好的建模里,应该能带来收益,这也是ODPO的思路,而两个response之间的差距就是offset。
DPO with an Offset
给 \(\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_w),\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_l)\) 分别加上Gumbel noise,即得到
\[\tilde{r}_w\sim\operatorname{Gumbel}(\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_w),1)\]
\[\tilde{r}_l\sim\operatorname{Gumbel}(\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_l),1)\]
论文中证明了
\[p\big(\tilde{r}_w-\tilde{r}_l>\Delta_r\big)=\sigma(\Delta_{\hat{r}_\theta}-\Delta_r)\]
基于此,ODPO的损失函数表达成
\[\mathcal{L}^{\mathrm{ODPO}}(\boldsymbol{\theta})=-\underset{(\boldsymbol{x},\boldsymbol{y}_w,\boldsymbol{y}_l)\sim\mathcal{D}_{\mathrm{HF}}}{\operatorname*{\mathbb{E}}}\left[\log\sigma{\left(\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_w)-\hat{r}_{\boldsymbol{\theta}}(\boldsymbol{x},\boldsymbol{y}_l)-\Delta_r\right)}\right]\]
这相当于要求preferred response的estimated reward要比dispreferred response的estimated reward大,且要大offset值这么多。
当offset=0的时候,ODPO的损失等价于DPO的损失。
ODPO的这个做法和softmax margin loss/marginal loss有些相似,都是在原来loss的基础上,加上一个margin,加大对靠得比较近的数据对的penalization的力度。
ODPO里,offset是两个response之间的actual reward的increasing scaling function。
\[\Delta_r=\alpha\mathbf{f}\big(\mathrm{score}(\boldsymbol{x},\boldsymbol{y}_w)-\mathrm{score}(\boldsymbol{x},\boldsymbol{y}_l)\big)\]
其中 \(\alpha\) 是超参。
实验
论文在几个下游任务上做了实验。
sentiment control
首先是sentiment control的任务,即要求模型输出positive的response。
先用GPT2-Large在IMDB dataset做了finetune,获得SFT模型。论文用一个现成的sentiment classifier作为reward的打分模型,给response分别打分,分数如下计算
\[r_{negative}(\boldsymbol{x},\boldsymbol{y}) = 1-p(\text{negative}\mid\cdot)\]
\[r_{positive}(\boldsymbol{x},\boldsymbol{y}) = 1+p(\text{positive}\mid\cdot)\]
有了reward打分数据之后,还要构造偏好数据对。这里把同一个prompt下生成的所有reward分数不同的response进行排列组合,获得偏好数据对。
对于DPO,有这些偏好数据对就够了。而ODPO还需要一个offset,按如下方式计算:
\[\Delta_r=\log\left(r(\boldsymbol{y}_w)-r(\boldsymbol{y}_l)\right)\]
实验里把 \(\alpha\) 设为1。
实验中使用两个不同的random seed,从SFT模型里进行采样,从而得到了2份不同的偏好数据。
而 \(\beta\) 使用了14个不同的取值 \(\{0.1,0.2,\ldots,1\}\cup\{1,2,3,4,5\}\) 进行实验。
论文在2份数据集下分别使用不同的数据量进行训练(5000,7500,10000),这样DPO和ODPO分别有2×3×14=84个实验。
每个实验计算模型生成结果的sentiment打分,以及和SFT模型的KL divergence。结果如下图
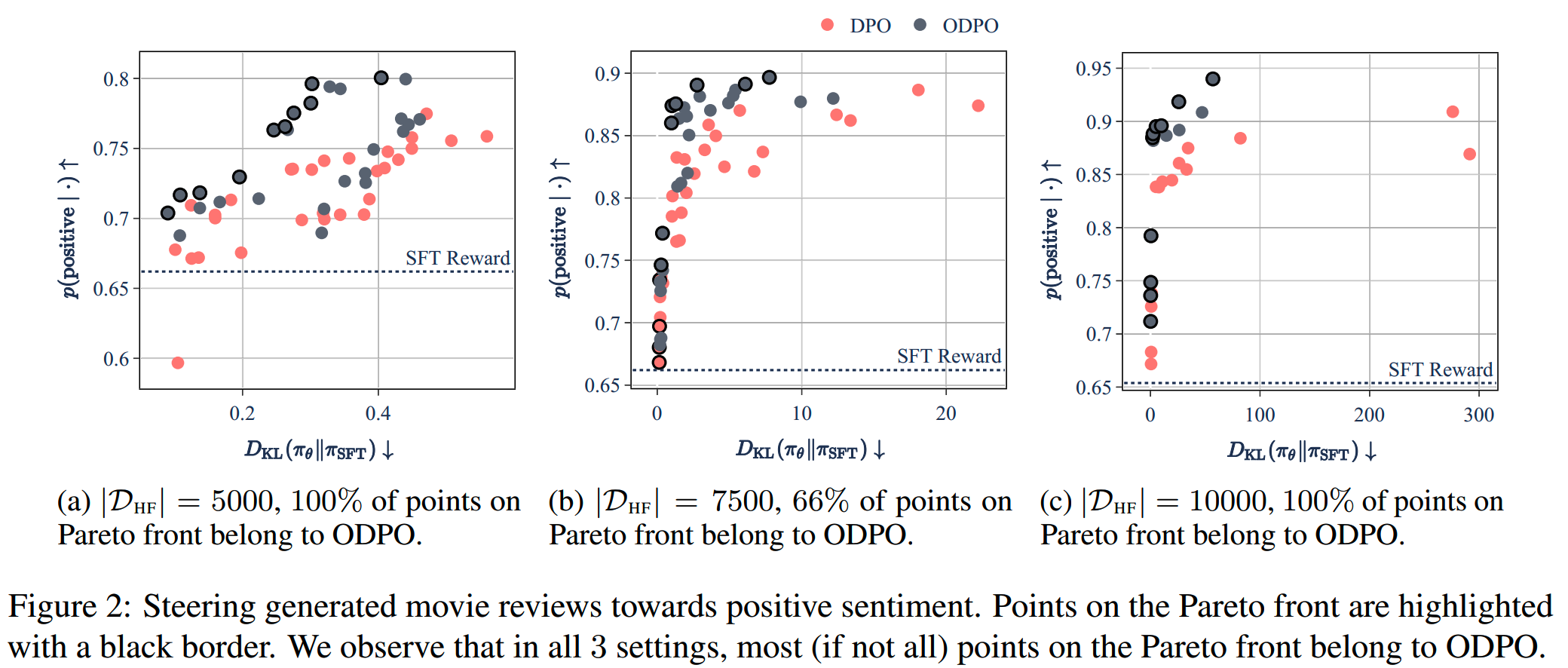
我们希望模型在sentiment的打分上越高越好,同时不要和SFT模型有太大的差距,因此越靠近左上角的点越符合我们的要求。从结果上看,ODPO比DPO更好一些。
toxicity control
toxicity control任务和sentiment control类似,要求模型的response的毒性尽量低。
这次使用GPT-neo-2.7b模型,\(\beta\) 的取值范围为 \(\{0.05,0.1,0.2,0.3,0.4,0.5\}\),使用从REALTOXICITYPROMPTS数据集里抽样的10000个毒性评分大于0.3的prompt。
结果如下
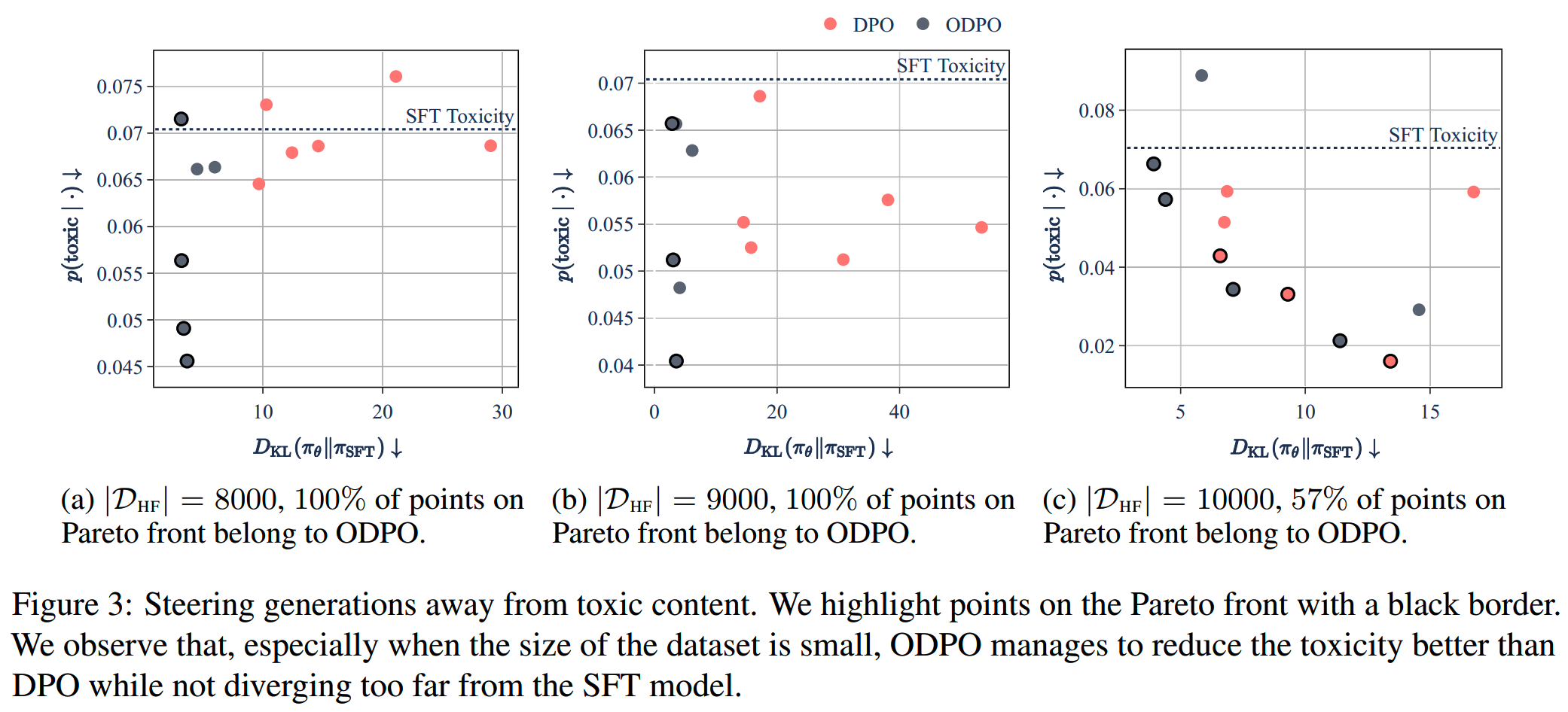
在数据量较少的情况下(8000 & 9000),ODPO效果更明显好。
summarization
摘要任务使用REDDIT TL;DR数据集,使用的模型是GPTJ-6B。
DPO和ODPO训练后的评分:抽了100条测试prompt,用不同的temperature生成结果,并用GPT-4进行评分对比。结果如下
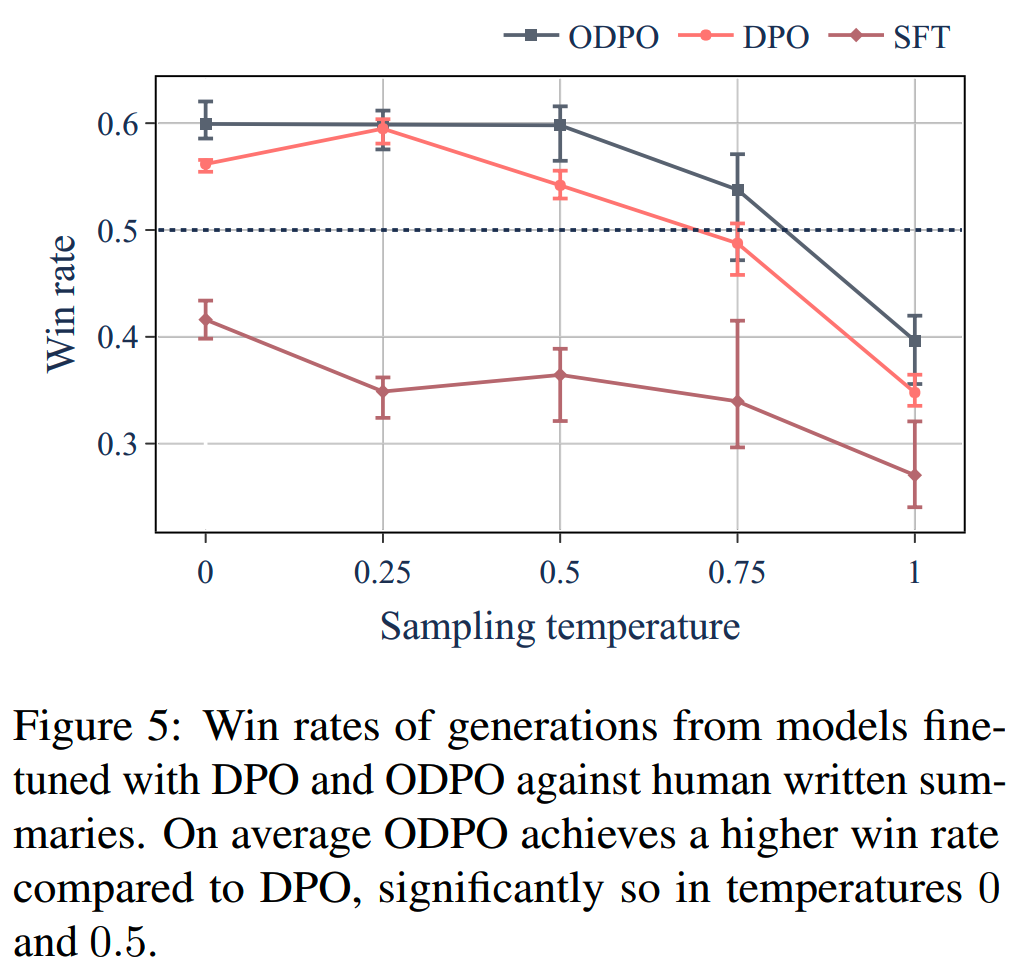
DPO和ODPO都比SFT好,并且在temperature比较低的设置下,DPO和ODPO都比human-written的结果好。
消融实验:scaling function
前面实验的offset都是用reward差值的log值,这里使用其他两种计算方式进行对比
\[\Delta_r=\log r(\boldsymbol{y}_w)-\log r(\boldsymbol{y}_l)\]
\[\begin{array}{rcl}\Delta_r=r(\boldsymbol{y}_w)-r(\boldsymbol{y}_l)\end{array}\]
使用5000对sentiment control的数据,\(\beta \in \{0.1,0.2,\ldots,0.9\}\cup\{1,2,3,4,5\}\)。
对比结果如下
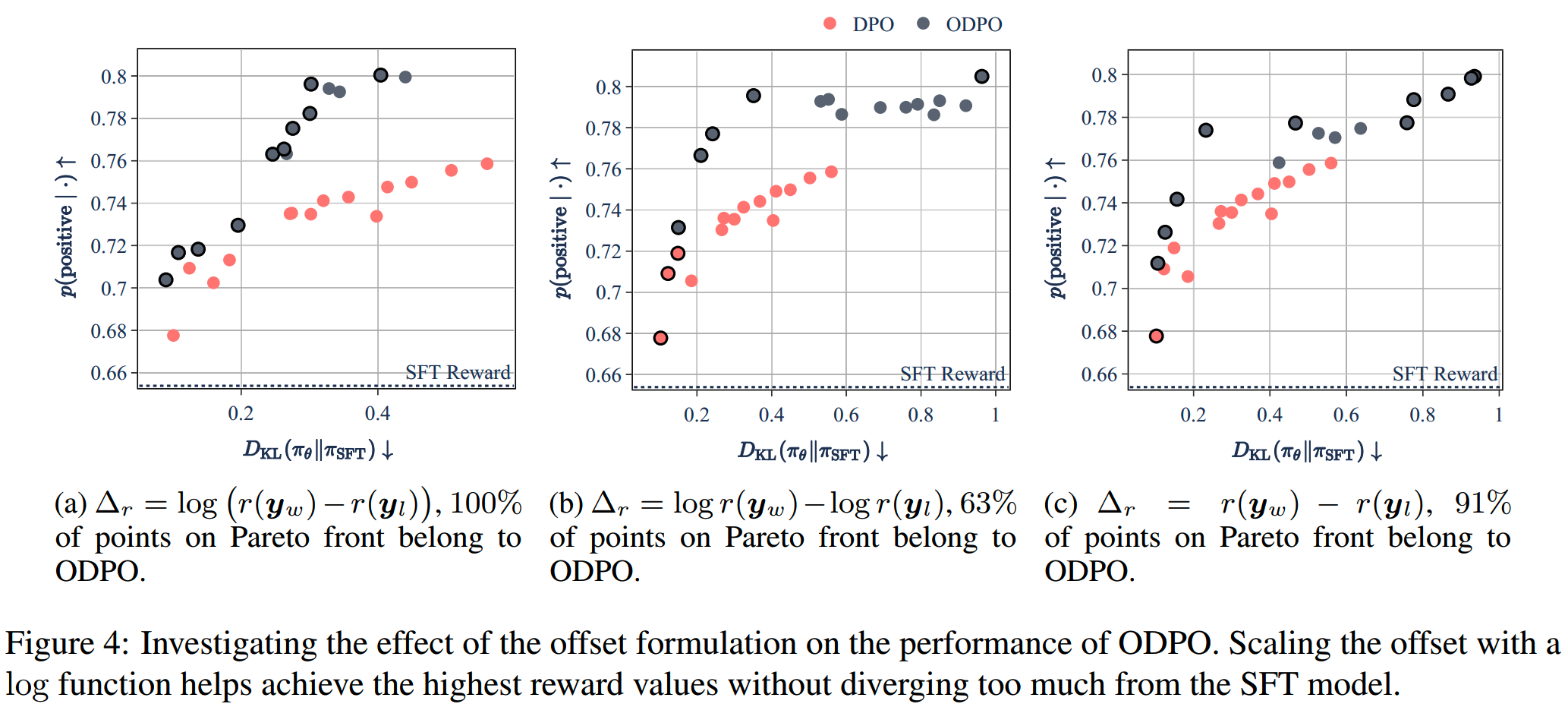
使用log scaling的ODPO在KL divergence更小的时候(0.4)可以达到0.8的reward,而没有使用log scaling的模型需要再更大的KL divergence下才能达到通用的reward。
消融实验:α
同样使用7500对sentiment control的数据,\(\beta=0.5\),改变\(\alpha\in\{0.0,0.1,0.2,0.3,0.5,0.8,1.\}\)。
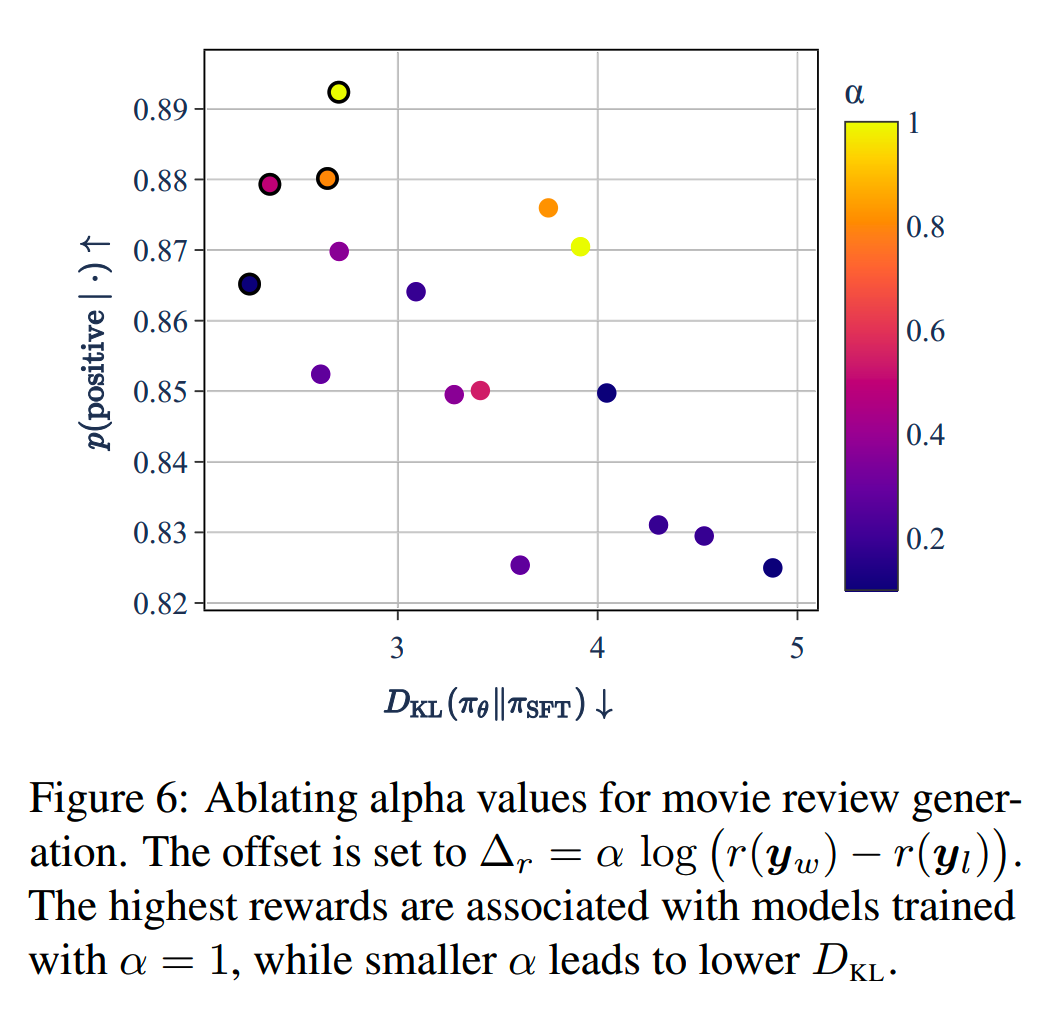
发现更高的 \(\alpha\) 会使得模型更多偏离SFT模型,并带来更高的reward值。
小结
ODPO在DPO的基础上加入了offset,在实现上并不复杂,而且能带来一些收益。
略有瑕疵的是ODPO的实验覆盖面并不太全,也没有使用LLAMA等更强大的模型进行实验。
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

【往期文章】
MoE模型的前世今生
LLM长上下文的问题
解锁大模型长上下文能力
大模型推理窗口-从有限到无限大
理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
大模型偏好对齐-DPO
Yi技术报告-划重点看细节
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding
window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)
Reference
【1】Direct Preference Optimization with an Offset https://arxiv.org/pdf/2402.10571