大模型推理加速-投机解码

发表于 2024-05-13 更新于 2024-05-25 分类于 CS ， NLP ， LLM 本文字数： 10k 阅读时长 ≈ 18 分钟

【本文已在同名微信公众号 / 知乎 / 个人博客linsight.cn 上线】

大语言模型虽然效果很好，但是推理时，朴素的自回归解码策略需要逐个串行解码，耗时较长，这给用户的耐心带来了很大挑战。如今各家大模型提供商基本都有对外提供大模型的体验平台，而模型的推理效率自然也成了一个重要的竞争点。

speculative decoding，译作投机解码，就是推理加速的一个比较巧妙的方案。本篇将介绍投机解码的基础思路。

背景

2022年11月，Google在《Fast Inference from Transformers via Speculative Decoding》里提出投机解码的策略；DeepMind稍晚一点，在2023年初的《Accelerating Large Language Model Decoding with Speculative Sampling》也提出了一样的解码策略。（以这两家的关系，很可能私底下就沟通过这个idea了）Google的论文相比DeepMind的，做了更多的实验和分析，更为详尽一些。

在speculative decoding之前，研究人员已经在模型推理加速这个方向做了不少工作：
- 模型蒸馏：以Hinton的《Distilling the Knowledge in a Neural Network》为代表，以及后面衍生出的各种蒸馏方法（参考《Knowledge Distillation: A Survey》），可以把规模更大的、性能更强的模型的能力，部分迁移到规模较小的模型上，在效果上相比直接训练小模型有一定的提升。transformer上蒸馏相关的经典工作有《TinyBERT: Distilling BERT for Natural Language Understanding》和《DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter》等。
- 模型量化：如《Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations》、《LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale》、《Zeroquant: Efficient and affordable post-training quantization for large-scale transformers》等，把模型参数量化到int8、int4以及更低的精度，在减少空间需求的同时，最大化地保持模型的推理效果。
- 高效模型结构设计：如使用稀疏层的《Sparse is Enough in Scaling Transformers》，减少KV缓存需求的MQA《Fast Transformer Decoding: One Write-Head is All You Need》、GQA《《GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints》》以及最近DeepSeek-V2中的MLA等，还有通过进化算法进行高效架构搜索的工作《Primer: Searching for Efficient Transformers for Language Modeling》。

以上这些做法对不同的输入一视同仁，采用一个全局来看有收益的方案来统一处理，达到推理加速的目的。

相对地，也有一些其他的方案，认为不是每一步推理都适合一样处理：某些推理step需要大模型，而另一些step只需要高效的小模型，从而根据输入，动态地决定模型参与计算的参数，相关工作有：
- 《Dynamic Neural Networks: A Survey》
- 《Adaptive Attention Span in Transformers》
- 《Consistent Accelerated Inference via Confident Adaptive Transformers》
- 《Why should we add early exits to neural networks?》
- 《Controlling Computation versus Quality for Neural Sequence Models》
- 《The Right Tool for the Job: Matching Model and Instance Complexities》
- 《Depth-Adaptive Transformer》
- 等

MoE也属于动态激活的方案之一。

而《Training compute-optimal large language models》的scaling law则指出模型规模没有原先预想的影响那么大，可以通过增加训练数据等方法让小模型逼近大模型的效果。

以上这些方案虽然可以在一定程度上提升推理效率，但是要么需要重新训练模型，要么对模型的效果有损害。

也有一些方案在解码的方法上进行优化，比如《Blockwise Parallel Decoding for Deep Autoregressive Models》和《Lossless Acceleration for Seq2seq Generation with Aggressive Decoding》。

speculative decoding也是一个在解码策略上进行优化的方法。投机解码可以在不用训练原模型的基础上，提升2x-3x的推理速度，并且保证结果和原模型完全一致，没有任何效果损失。

speculative decoding算法

回想一下，自回归语言模型在训练的时候，在每一个位置，会根据当前及前面所有的token，预测下一个token。由于强制学习的特性，所有token可以一起训练。在某种特别的情况下，模型对当前的输入拟合得特别好，就有可能出现每个token的预测，都完美命中下一个输入token的情况。举个例子：

1
2
3

位置：一  二  三  四
输入：我  爱  中  国
输出：爱  中  国  EOS

而在推理的时候，这种依赖前面所有token的特性，使得自回归模型只能一个一个串行地解码：

step1：输入“我”，输出“爱”；
step2：输入“我爱”，输出“中”；
step3：输入“我爱中”，输出“国”；
step4：输入“我爱中国”，输出“EOS”；

现在，假设我们有一个神奇海螺，你只要输入“我”，就会输出“爱中国 EOS”四个token作为草稿，我们就可以拿着这四个draft token一起放到原来的模型，跑一下各个位置的输出，进行验证，跟训练时的前向推理一样：

1
2
3

位置：一  二  三  四
输入：我  爱  中  国
输出：爱  中  国  EOS

然后就会发现模型的输出和神奇海螺给出的草稿完全一致，那就相当于我们只进行了一次模型推理，就解码了四个token，并且和原模型的效果完全一致。并且一般情况下，模型对一个位置进行预测和对四个位置进行预测的耗时基本没有太大的差异，也就是说在这个例子下，模型解码速度提升到了将近4倍。

当然，神奇海螺不会总是能够给出和模型一模一样的结果，除非它就是模型本身。因此，在上面这个例子中，输入“我”之后，神奇海螺有可能给出的是“爱中华 EOS”这四个draft token。这种情况下，我们把这些token一起输入到模型进行验证

1
2
3

位置：一  二  三  四
输入：我  爱  中  华
输出：爱  中  国  EOS

会发现神奇海螺给出的“爱”和“中”命中了模型的结果，但是“华”没对上。不过这种情况下，跑一次模型推理也能解码出两个token，推理效率依然有提升。

部分情况下，神奇海螺给出的结果也可能完全跑偏，比如给它输入“我”，它有可能输出“叫小明”，这就和原模型一个都没对上。但是只要统计上，神奇海螺给出的草稿平均命中token数 > 0，我们就有机会获得推理加速。

使用神奇海螺的这个思路其实就是speculative decoding的主要思路，而你肯定也已经猜到了，神奇海螺其实就是一个规模比较小的模型，论文中把它称为approximation model或者draft model，而我们想要加速的原模型则叫target model。

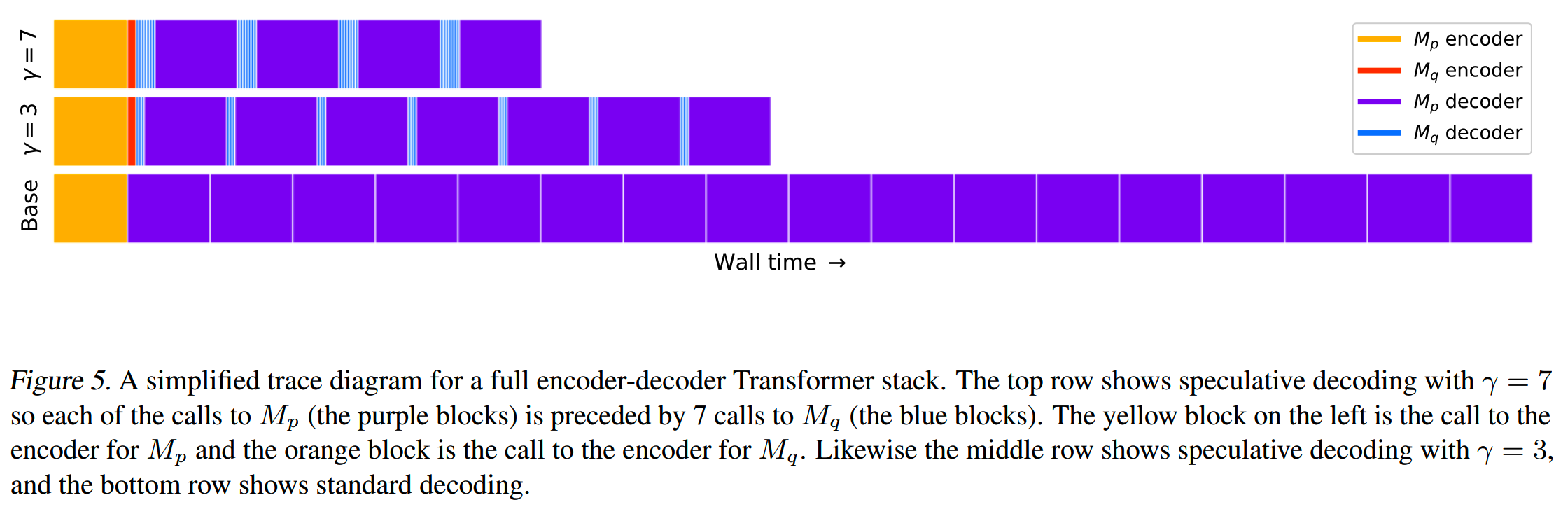
论文给出的一个例子如下

绿色的就是approximation model给出并命中target model验证结果的token，红色的是错误的token，蓝色则是修正后的token。

在这个例子中，target模型只推理了9次，就解码出了38个token，推理速度获得了较大提升。

看完了例子，现在对投机解码算法给出正式的描述。

\(M_p\) 是target model， \(M_q\) 是approximation model，prefix是当前的输入。

首先 \(M_q\) 给出 \(\gamma\) 个draft token，然后 \(M_p\) 并行地对这 \(\gamma\) 个draft token进行验证，根据验证结果，按顺序把通过验证的token加入到当前序列中；如果出现被 \(M_p\) 拒绝的token，这些token则按规则重新抽样。

Google论文给出的投机解码算法描述如下图。

（DeepMind版本的算法描述在下面）

这里注意，投机解码单次运行能解码的token数量，除了这 \(n\) 个被接受的draft token，还有 \(M_p\) 对这些草稿进行验证时顺便推理出来的一个额外token，因此最终可以得到 \(n+1\) 个token。因此如果approximation model每次给出 \(\gamma\) 个draft token，理论上最多可以获得 \(\gamma+1\) 新解码token，而最少也能有1个（来自target模型）。

投机解码的原理大致就是这样，思路还是很巧妙的，但是要实际应用还有几个问题需要解决，比如：
- 关于投机采样speculative sampling：target model怎么对approximation model给出的token进行验证？在一个draft token被拒绝之后，怎么重新采样？
- 怎么选择 \(\gamma\) 才合理？
- 怎么选择approximation model，用什么指标表征approximation model的质量？

另外，DeepMind论文的给出投机解码算法如下，可以对照Google的算法，方便理解。（DeepMind所用的符号有所不同，本篇采用Google论文的符号描述。）

里面的 \((.)_+\) 操作表示 \((f(x))_+=\frac{\max(0,f(x))}{\sum_x\max(0,f(x))}\) 。

speculative sampling的正确性

我们希望投机解码的最终结果，和target model自回归解码的结果一致，即完全无损，因此需要对投机采样做一些设计和分析。

首先，当前在transformer的解码上已经有很多策略，包括但不限于argmax、top-k采样、使用温度等。而大部分操作都是在logits上进行操作，这相当于改变了模型的输出分布。而在最终分布上的采样操作，都是相同的。因此我们可以只在朴素的标准采样上进行分析，而结果可以推广到其他的解码策略上。

假设 \(p(x)\) 是target model \(M_p\) 在当前输入下的分布， \(q(x)\) 是approximation model \(M_q\) 在当前输入下的分布。

投机解码的做法是，先采样 \(x\sim q(x)\)，如果 \(q(x)\leq p(x)\)，就保留 \(x\)，否则就以 \(1-\frac{p(x)}{q(x)}\) 的概率拒绝 \(x\)，并在分布 \(p'(x)=norm(max(0,p(x)-q(x)))\) 对被拒绝的 \(x\) 重新采样，并结束当前的投机解码。

其中 \(norm(max(0,p(x)-q(x)))=\frac{\max(0,p(x)-q(x))}{\sum_x\max(0,p(x)-q(x))}\) 。

看起来并不复杂。一个问题是，为什么这样从 \(q(x)\) 采样之后，我们得到的结果符合分布 \(p(x)\)？即按这样的概率进行拒绝之后，结果和target model自己解码一样？

从公式上来说，approximation model的抽样有 \(\tilde{x}\sim q\)。假设 \(X\) 是最终结果，我们的目标就是证明 \(\mathbb{P}(X=x)=p(x)\)。

而要使得 \(X=x\)，只有 \(\tilde{x}=x\) 且 \(\tilde{x}\) 被接受，或者在 \(\tilde{x}\) 被拒绝之后重新采样到 \(\tilde{x}=x\) 两种情况，即有

\[\mathbb{P}(X=x)\\=\mathbb{P}(\tilde{x}=x)\mathbb{P}(\tilde{x}\textit{ accepted}|\tilde{x}=x)\\+\mathbb{P}(\tilde{x}\textit{ rejected})\mathbb{P}(X=x|\tilde{x}\textit{ rejected})\]

对于第一项，有

\[ \begin{aligned} &\mathbb{P}(\tilde{x}=x)\mathbb{P}(\tilde{x}\text{ ассерґе}d|\tilde{x}=x)\\=&q(x)\min\left(1,\frac{p(x)}{q(x)}\right)\\=&\min\left(q(x),p(x)\right) \end{aligned} \]

而第二项里

\[\begin{gathered} \mathbb{P}(\tilde{x}\textit{ rejected})=1-\mathbb{P}(\tilde{x}\textit{ accepted}) \\ =1-\sum_{x^{\prime}}\mathbb{P}(X=x^{\prime},\tilde{x}\text{ ассерґе}d) \\ =1-\sum_{x'}\min(q(x'),p(x')) \\ =\sum_{x'}\max(0,p(x')-q(x')) \\ \end{gathered}\]

上式第三行到第四行的解释：第三行相当于计算1减区域b的面积，而区域a+区域b的面积和为1，因此第三行相当于区域a的面积，即 \(\sum_{x'}\max(0,p(x')-q(x'))\)。

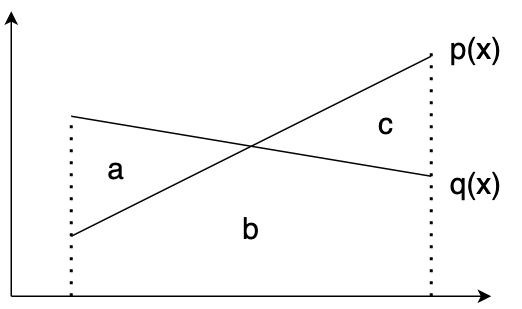
从采样规则，有

\[\mathbb{P}(X=x|\tilde{x}\text{ rejected})=\frac{\max(0,p(x)-q(x))}{\sum_x\max(0,p(x)-q(x))}\]

因此

\[\mathbb{P}(\tilde{x}\text{ rejected})\mathbb{P}(X=x|\tilde{x}\text{ rejected})=\max(0,p(x)-q(x))\]

最终有

\[\mathbb{P}(X=x)\\=\min(q(x),p(x))+\max(0,p(x)-q(x))\\=p(x)\]

因此按照前面设计的规则进行采样，就能保证结果和target model自己解码出来的一样。

approximation model的评估

approximation model的一个采样 \(x\sim q(x)\) 被target model接受的概率为 \(\beta\)，我们把这个概率叫acceptance rate接受率。

那么其期望值 \(E(\beta)\) 就是approximation model对target model拟合质量一个很好的评估指标。

\(E(\beta)\) 越大，每个token被接受的概率越大，那么每次投机解码能获得的输出token越多。

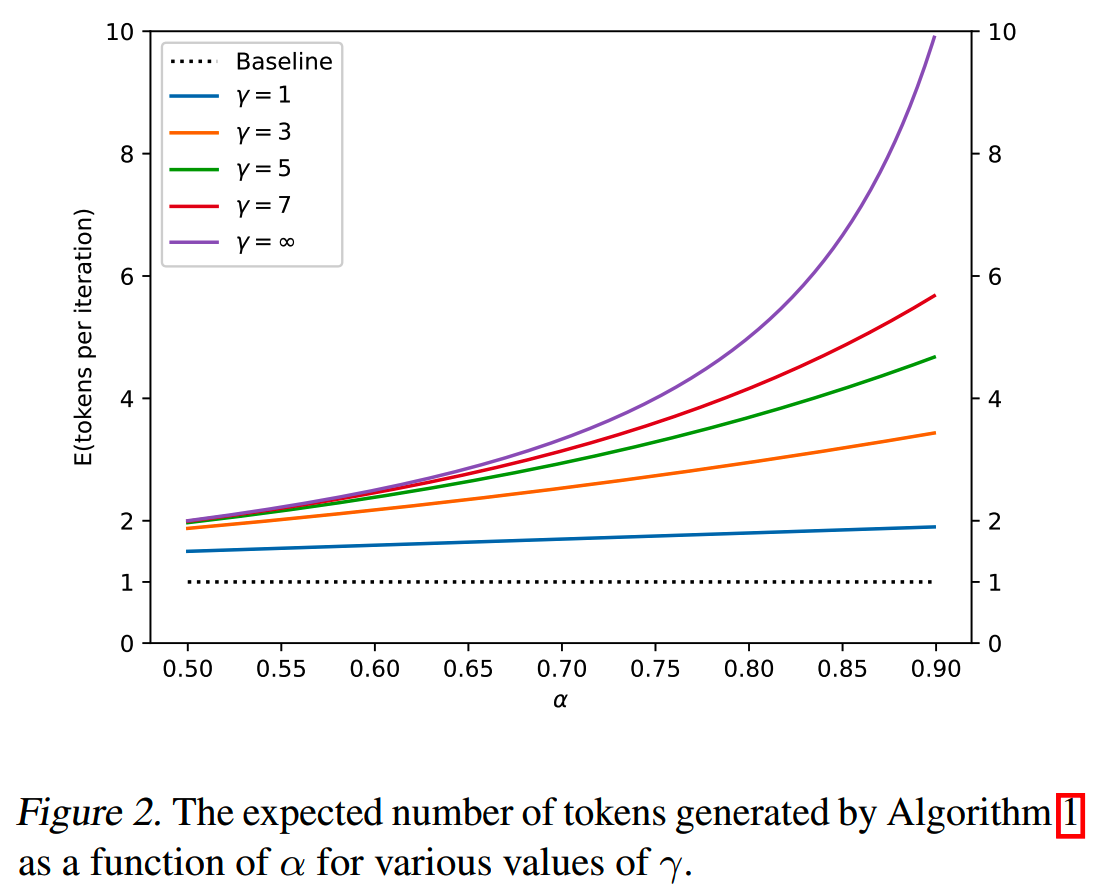
我们令 \(\alpha=E(\beta)\)，并且为简化起见，假设 \(\beta\) 的分布是i.i.d.的，那么跑一次投机解码能够获得的token数量是一个capped geometric variable，其期望值如下式

\[E(\#\textit{ generated tokens})=\frac{1-\alpha^{\gamma+1}}{1-\alpha}\]

不同 \(\gamma\) 下的图像如下

而 \(\alpha\) 是可以推算的。

首先定义一个 \(M_p\) 和 \(M_q\) 之间的divergence \(D_{LK}\)

\[\begin{aligned}D_{LK}(p,q)=\sum_x|p(x)-M(x)|=\sum_x|q(x)-M(x)|\end{aligned}\]

其中 \(M(x)=\frac{p(x)+q(x)}2\)。

而

\[ \begin{aligned} &\sum_x|p(x)-M(x)|\\=&\sum_x\frac{|p-q|}{2}\\=&1-\sum_x\frac{p+q-|p-q|}2\\=&1-\sum_x\min(p(x),q(x)) \end{aligned} \]

因此有

\[D_{LK}(p,q)=1-\sum_x\min(p(x),q(x))\]

\(D_{LK}(p,q)\)越小，则 \(M_p\) 和 \(M_q\) 越相近。如果 \(D_{LK}(p,q)=0\)，说明 \(p=q\)；如果 \(D_{LK}(p,q)=1\)，说明 \(p\) 和 \(q\) 两个分布完全没有交叉的部分。

根据 \(\beta\) 的定义，有

\[ \begin{aligned} \beta=&E_{x\sim q(x)}\begin{cases}1&q(x)\leq p(x)\\\frac{p(x)}{q(x)}&q(x)>p(x)\end{cases}\\ =&E_{x\thicksim q(x)}\min(1,\frac{p(x)}{q(x)})\\ =&\sum_x\min(p(x),q(x))\\ =&1-D_{LK}(p,q) \end{aligned} \]

最终得到

\[\alpha=E(\beta)=1-E(D_{LK}(p,q))=E(\min(p,q))\]

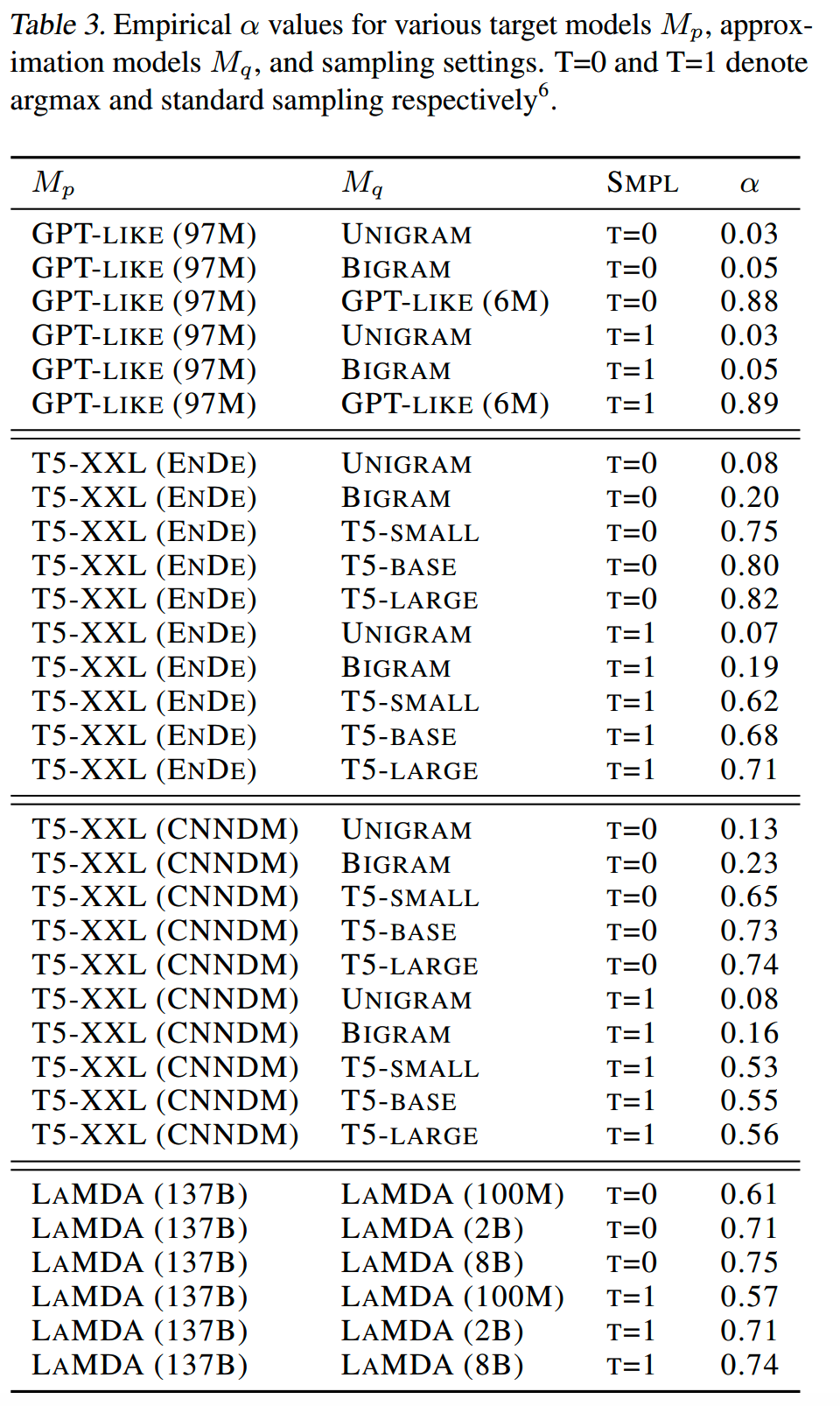
实验中，不同approximation model和target model之间测得的 \(\alpha\) 值如下表所示

耗时优化的分析

定义cost coefficient \(c\)，表示 \(M_q\) 单次推理和 \(M_p\) 单次推理的比值。

和仅与模型相关的 \(\alpha\) 不同，\(c\) 的具体值会受到硬件、推理框架等影响。在论文的实验中 \(c\) 的值大部分小于0.05。

假设 \(M_p\) 每次推理所需的时间为 \(T\)，则一次投机解码所需的时间为 \(Tc\gamma+T\)。

根据前面的推算，投机解码每次能获得的token数为 \(E(\#\textit{ generated tokens})=\frac{1-\alpha^{\gamma+1}}{1-\alpha}\) 个，因此每个token所需的时间为 \(\frac{(c\gamma+1)(1-\alpha)}{1-\alpha^{\gamma+1}}T\)。综上，使用投机解码在推理时间上的improvement factor为

\[\frac{1-\alpha^{\gamma+1}}{(1-\alpha)(\gamma c+1)}\]

只要 \(\alpha>c\)，就一定存在能提升解码效率的 \(\gamma\)，并且improvement factor至少为 \(\frac{1+\alpha}{1+c}\)（\(\gamma=1\)时）。

计算成本的分析

\(M_p\) 同时对 \(\gamma+1\) 个token进行验证。如果一个token被接受了，那么推理效率就获得了提升；如果token被拒绝了，那么相关的计算就没有实际收益，就会有计算的“浪费”。

假设 \(\hat{c}\) 是 \(M_q\) 和 \(M_p\) 计算一个token的arithmetic operations的比例，\(\hat{T}\) 是 \(M_p\) 解码一个token所需的arithmetic operations。

那么一次投机解码的计算量就是 \(\hat{T}\hat{c}\gamma+\hat{T}(\gamma+1)\)，这个计算量除以投机解码每次获得的token数 \(\frac{1-\alpha^{\gamma+1}}{1-\alpha}\) 就得到平均每个token的计算量为 \(\hat{T}\frac{(1-\alpha)(\gamma\hat{c}+\gamma+1)}{1-\alpha^{\gamma+1}}\)。

\(\alpha\) 越大，\(\frac{(1-\alpha)(\gamma\hat{c}+\gamma+1)}{1-\alpha^{\gamma+1}}\) 这个比值越小，平均计算成本越低。

另外，使用投机解码减少了KV cache和显存的读写。

\(\gamma\) 的选择

给定 \(\alpha\) 和 \(c\)，最佳的 \(\gamma\) 应该最大化walltime improvement factor \(\frac{1-\alpha^{\gamma+1}}{(1-\alpha)(\gamma c+1)}\)。

下图给出不同 \(\alpha\) 和 \(c\) 下，最佳的 \(\gamma\) 值

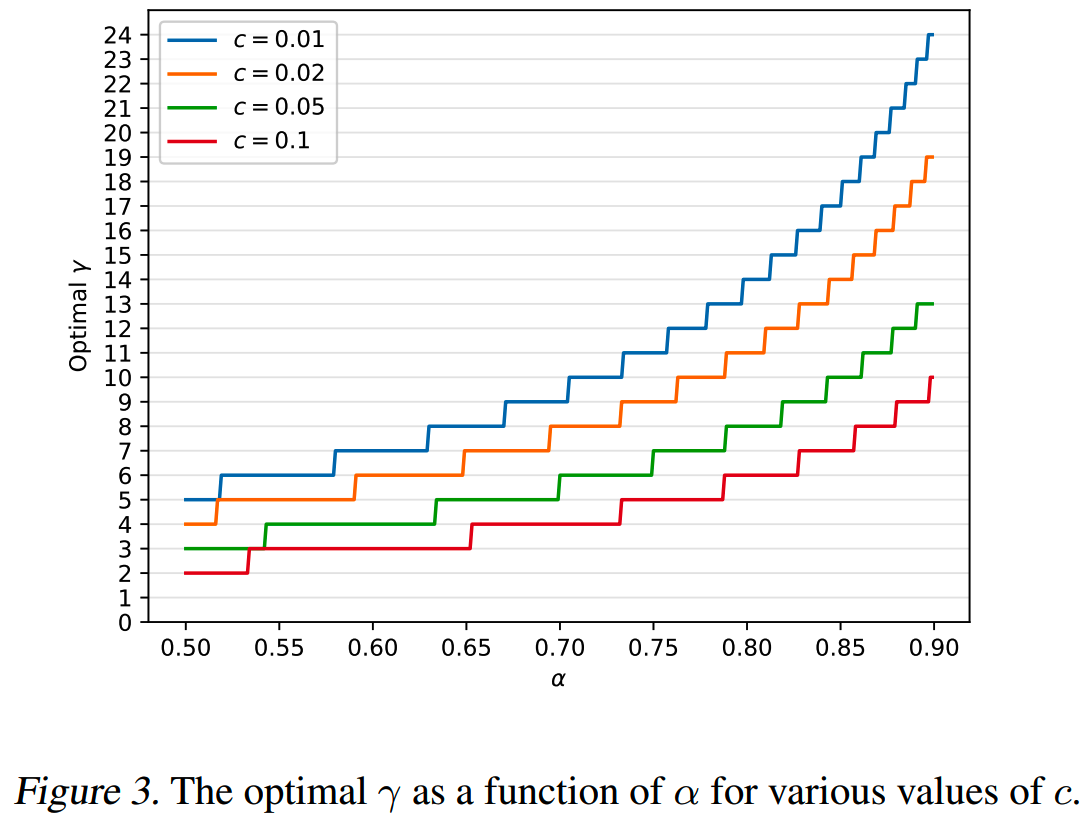
推理速度和总计算量之间有tradeoff，即增大 \(\gamma\) 会提升推理速度，同时也会带来更多的计算成本，如下所示

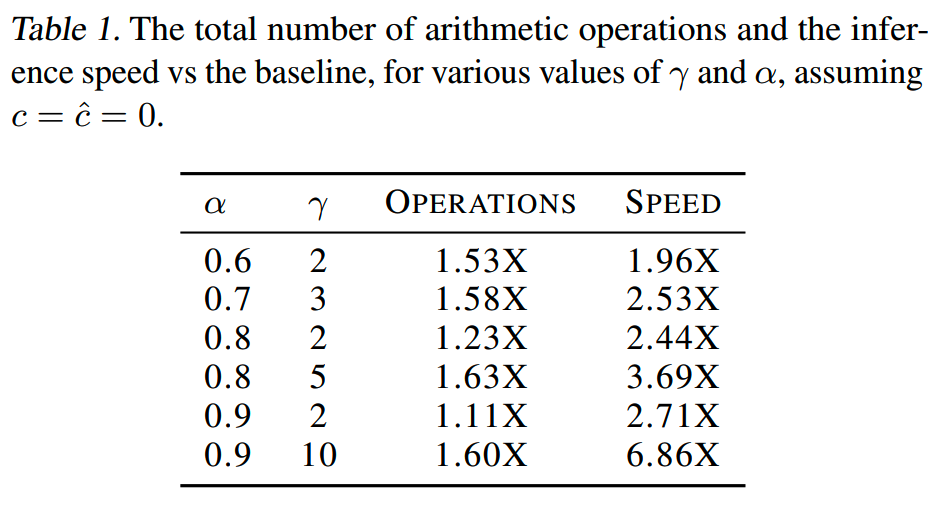
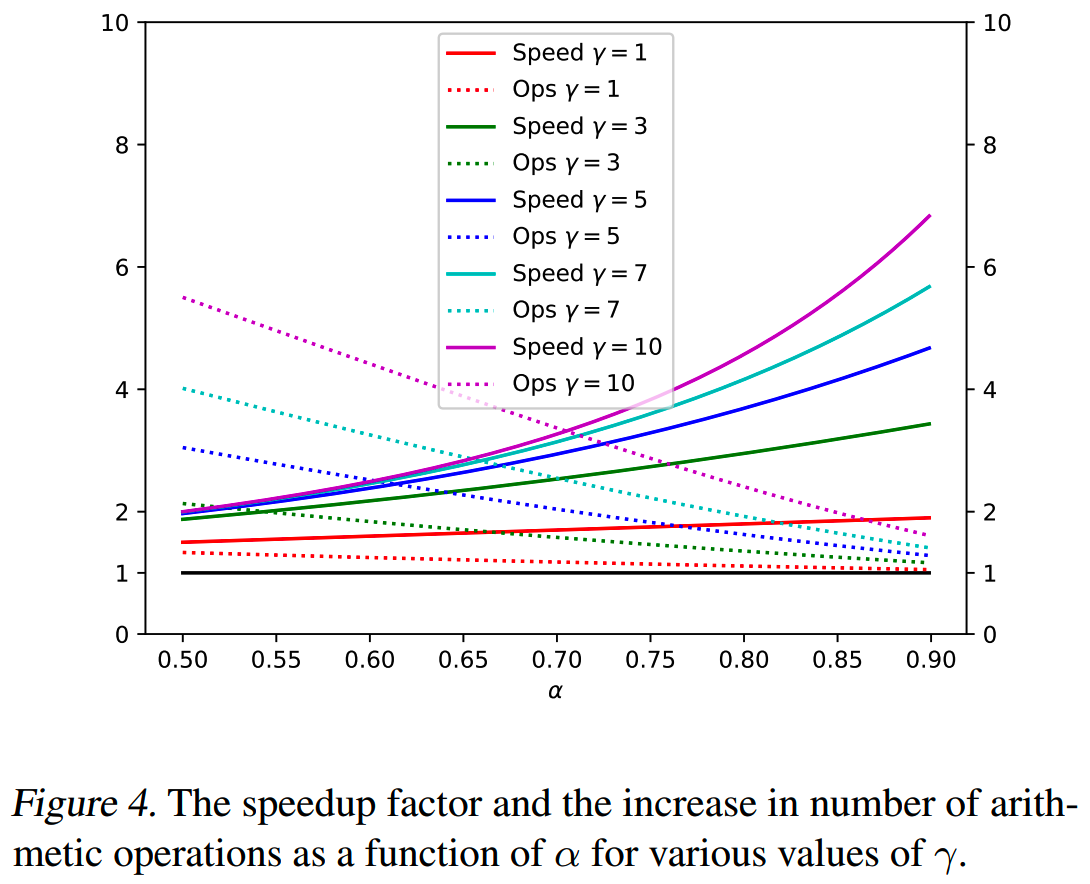
实际上，\(\beta\) 并不是固定的常数，因此实际上我们可以通过在投机解码的过程中预测 \(\beta\) 值来选择 \(\gamma\)，这是未来的一个改进方向。

approximation model的选择

论文的实验中，一部分使用现成的模型作为approximation model。这种情况下，让approximation model的参数规模比target model小两个数量级是比较好的选择，能够平衡推理加速和计算量。

有趣的是，即使使用很简单的模型，比如n-gram模型作为approximation model，也能获得不错的 \(\alpha\) 值。

另外，在一些特殊的任务，比如摘要任务，由于生成结果往往会从输入的原文里摘取内容，因此使用一个会从输入里copy token的approximation model可能会得到较高的 \(\alpha\) 值。

approximation model的另一个选择是如《Blockwise parallel decoding for deep autoregressive models》使用的非自回归模型。

实验

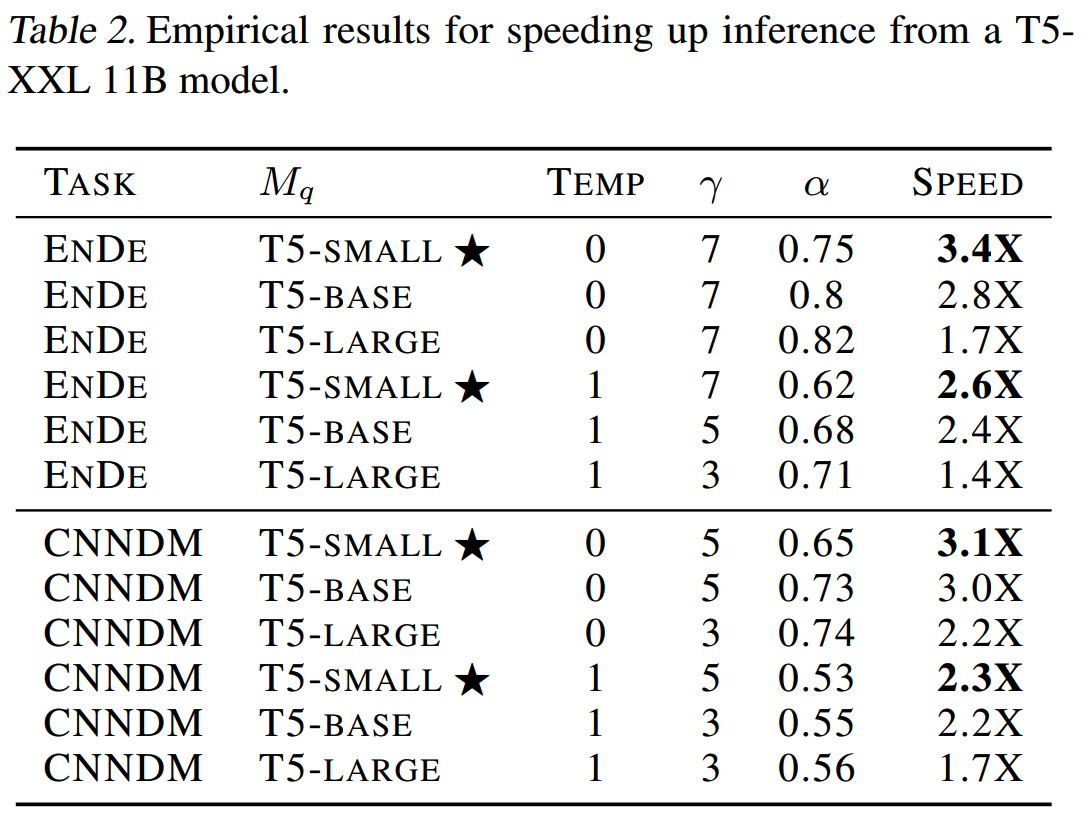
论文在翻译任务和摘要任务上测试了投机解码的效果。使用了T5的较小规模模型作为approximation model，来加速T5-XXL的推理，效果如下表，最高能达到3倍+的推理加速。

此外，论文对更多样的模型组合测试了 \(\alpha\) 值，如下表所示

可以观察到，比target model小几个数量级的approximation model倾向于产生介于0.5和0.9之间的 \(\alpha\) 值。还注意到，对于所有模型，用于采样的分布越尖（即T比较小，如argmax）， \(\alpha\) 值越高。

小结

投机解码可以在完全无损的情况下，把推理速度提升2~3倍
即使使用最简单的n-gram模型，也能在投机解码的策略下获得推理速度提升
正常来说，使用比target model小两个数量级的approximation model就有较好的效果

读到这了，来一发点赞收藏关注吧~

博客：http://www.linsight.cn/
知乎：Linsight
微信公众号：Linsight

【往期文章】

MoE模型的前世今生
 LLM长上下文的问题
 解锁大模型长上下文能力
 大模型推理窗口-从有限到无限大
 理解Attention:从起源到MHA,MQA和GQA
Yi技术报告-划重点看细节
 transformer中normalization的二三事
 从代码实现看normalization-到底做了什么
 稀疏注意力计算:sliding window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)

Reference

【1】Fast Inference from Transformers via Speculative Decoding https://arxiv.org/abs/2211.17192
【2】Accelerating Large Language Model Decoding with Speculative Sampling https://arxiv.org/abs/2302.01318