从代码实现看normalization-到底做了什么

发表于 更新于 分类于 ， ， 本文字数： 19k 阅读时长 ≈ 34 分钟

【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】

之前在《transformer中normalization的二三事》从思路上梳理了关于常用的normalization的内容。发出之后收到了一些反馈，关于这些norm在实际使用中是怎么实现的，有一些疑问。

因此本篇从实现的角度，来看下这些norm在不同的场景下，到底做了什么。

代码已上传至https://github.com/Saicat/normalization_exp

二维数据

先看下二维数据的情况下normalization是怎么做的。二维数据一般可以对应到神经网络中的全连接层，比如CNN中分类网络最后几个特征层。

1
2
3
4
5
6
7
8
9
10
11
12
import torch
from torch import nn

# epsilon
eps = 1e-8

# 定义一个随机二维输入
batch_size = 3
feature_num = 4
torch.manual_seed(0)  # 设置随机种子，方便复现
inputs = torch.randn(batch_size, feature_num)
print('二维输入:\n', inputs)

这里定义了一个3×4的矩阵，相当于batch size=3，特征向量维度为4。得到的随机二维输入是

1
2
3
4
二维输入:
 tensor([[ 1.5410, -0.2934, -2.1788,  0.5684],
        [-1.0845, -1.3986,  0.4033,  0.8380],
        [-0.7193, -0.4033, -0.5966,  0.1820]])

batchnorm

用pytorch自带的BatchNorm1d对二维输入进行操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# torch自带的batchnorm
torch_bn = nn.BatchNorm1d(num_features=feature_num, affine=True)  # 注意完整的batchnorm要包括仿射变换

# 仿射变化初始化的weigh=1，bias=0，相当于没有进行变换，看不出效果
# 手动改成别的值，用于对比包含仿射变换的效果
torch.manual_seed(1)  # 设置随机种子，方便复现
torch_bn.weight = nn.Parameter(torch_bn.weight * torch.randn(feature_num))
torch_bn.bias = nn.Parameter(torch_bn.bias + torch.randn(feature_num))
print('weight:\n', torch_bn.weight)
print('bias:\n', torch_bn.bias, '\n')

# 结果
torch_normed = torch_bn(inputs)
print('torch bn结果:\n', torch_normed)

注意完整的batchnorm/layernorm等，是包括①归一化和②仿射变换（缩放+平移，也就是有可训练参数这部分）两步的。在BatchNorm接口中通过参数"affine"来决定是否进行放射变换。如果"affine"为False，相当于只是在某个维度上对数据进行了归一化处理。

而且pytorch中各种norm的接口初始化都把缩放系数初始化为1.0，平移系数初始化为0，相当于没有进行变换。为了把仿射变换的影响也一起对比，这里手动给缩放和平移系数都添加了一个随机数，变成如下数值

1
2
3
4
5
6
weight:
 Parameter containing:
tensor([0.6614, 0.2669, 0.0617, 0.6213], requires_grad=True)
bias:
 Parameter containing:
tensor([-0.4519, -0.1661, -1.5228,  0.3817], requires_grad=True)

这里缩放系数weight和平移系数bias的维度都是4，对应特征向量的维度。

输入矩阵用官方接口batchnorm之后得到的结果如下

1
2
3
4
5
torch bn结果:
 tensor([[ 0.4756,  0.0513, -1.6033,  0.4715],
        [-1.0197, -0.5421, -1.4535,  1.0937],
        [-0.8117, -0.0077, -1.5115, -0.4202]],
       grad_fn=<NativeBatchNormBackward0>)

接下来手动实现batchnorm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 手动bn

# 计算均值和标准差
mean = torch.mean(inputs, dim=0, keepdim=True)
print('均值:\n', mean)
std = torch.std(inputs, dim=0, keepdim=True, unbiased=False)
print('标准差:\n', std, '\n')

manual_normed = (inputs - mean) / (std + eps) * torch_bn.weight + torch_bn.bias
print('手动bn结果:\n', manual_normed)

# 手动操作和torch自带操作有点误差，<1e-4
isclose = torch.isclose(torch_normed, manual_normed, rtol=1e-4, atol=1e-4)
print(isclose)

在dim=0这个维度上计算均值和标准差，即对整个batch内所有sample的同一个feature，进行操作，获得结果如下

1
2
3
4
均值:
 tensor([[-0.0876, -0.6985, -0.7907,  0.5295]])
标准差:
 tensor([[1.1612, 0.4971, 1.0630, 0.2692]])

均值和标准差的维度也是和特征向量的维度一致。这里计算mean和std的时候keepdim设置为True和False都可以，最后都会自动broadcast。

一个要注意的点是，计算std的时候unbiased要设置为False，表明这里是对标准差的有偏估计，否则算出来的结果和torch的batchnorm接口不一致。

用手动计算出来的均值和标准差对输入进行归一化，再进行放射变换，得到手动计算的batchnorm结果如下

1
2
3
4
手动bn结果:
 tensor([[ 0.4756,  0.0514, -1.6033,  0.4715],
        [-1.0197, -0.5421, -1.4535,  1.0937],
        [-0.8117, -0.0077, -1.5115, -0.4202]], grad_fn=<AddBackward0>)

这里用torch.isclose接口验证官方batchnorm和手动计算的batchnorm是否相同

1
2
3
tensor([[True, True, True, True],
        [True, True, True, True],
        [True, True, True, True]])

为什么没有用equal，因为发现两个结果会有一点点误差，相对误差大概在1e-5~1e-4之间，应该是因为使用的eps不同导致。

layernorm

看下layernorm对于二维数据的操作，还是用同样的3×4的输入

使用torch官方接口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# torch自带的layernorm
torch_ln = nn.LayerNorm(normalized_shape=feature_num, elementwise_affine=True)  # 注意完整的layernorm要包括仿射变换

# 仿射变化初始化的weigh=1，bias=0，相当于没有进行变换，看不出效果
# 手动改成别的值，用于对比包含仿射变换的效果
torch.manual_seed(2)  # 设置随机种子，方便复现
torch_ln.weight = nn.Parameter(torch_ln.weight * torch.randn(feature_num))
torch_ln.bias = nn.Parameter(torch_ln.bias + torch.randn(feature_num))
print('weight:\n', torch_ln.weight)
print('bias:\n', torch_ln.bias, '\n')

# 结果
torch_normed = torch_ln(inputs)
print('torch ln结果:\n', torch_normed)

得到layernorm仿射变换的系数如下

1
2
3
4
5
6
weight:
 Parameter containing:
tensor([ 0.3923, -0.2236, -0.3195, -1.2050], requires_grad=True)
bias:
 Parameter containing:
tensor([ 1.0445, -0.6332,  0.5731,  0.5409], requires_grad=True)

维度依然是和特征向量的维度一致。

官方layernorm的结果是这样的

1
2
3
4
5
torch ln结果:
 tensor([[ 1.5120, -0.6001,  1.0604, -0.0392],
        [ 0.7249, -0.3772,  0.3331, -0.9155],
        [ 0.6645, -0.6209,  0.7693, -1.4324]],
       grad_fn=<NativeLayerNormBackward0>)

接下来手动实现一下，和官方结果作对比。

在dim=1计算均值和向量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 手动ln

# 计算均值
mean = torch.mean(inputs, dim=1, keepdim=True)
print('均值:\n', mean)
std = torch.std(inputs, dim=1, keepdim=True, unbiased=False)
print('标准差:\n', std, '\n')

manual_normed = (inputs - mean) / (std + eps) * torch_ln.weight + torch_ln.bias
print('手动ln结果:\n', manual_normed)

# 手动操作和torch自带操作有点误差，<1e-4
isclose = torch.isclose(torch_normed, manual_normed, rtol=1e-4, atol=1e-4)
print(isclose)

得到的均值和标准差是这样的

1
2
3
4
5
6
7
8
均值:
 tensor([[-0.0907],
        [-0.3104],
        [-0.3843]])
标准差:
 tensor([[1.3691],
        [0.9502],
        [0.3458]])

对输入进行归一化和仿射变换，结果如下，和官方接口结果一致

1
2
3
4
5
6
7
8
手动ln结果:
 tensor([[ 1.5120, -0.6001,  1.0604, -0.0392],
        [ 0.7249, -0.3772,  0.3331, -0.9155],
        [ 0.6645, -0.6209,  0.7693, -1.4325]], grad_fn=<AddBackward0>)
验证结果:
 tensor([[True, True, True, True],
        [True, True, True, True],
        [True, True, True, True]])

对比

对于二维输入，batchnorm和layernorm在做第①步归一化的时候，方向如下图

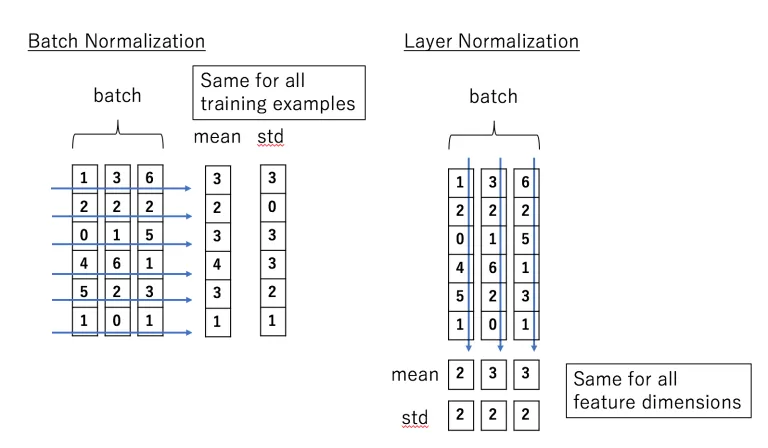
batchnorm在dim=0，即batch方向操作；而layernorm在dim=1，即特征向量内部进行操作。

但是无论是batchnorm还是layernorm，在做仿射变换的时候，使用的系数形状都和输入的特征向量相同，可以认为在放射变化这一步上，二者的操作是一样。

CV数据

再看下CV场景下的情况。

CV数据形状一般为[N,C,H,W]，N为batch size，C为channel即特征数，H和W分别是feature map的高和宽。先定义一个CV输入数据

1
2
3
4
5
6
7
8
# 定义一个随机四维输入，[N,C,H,W]
batch_size = 2
channel = 2
height = 2
width = 3
torch.manual_seed(3)  # 设置随机种子，方便复现
inputs = torch.randn(batch_size, channel, height, width)
print('四维输入:\n', inputs)

输入如下

1
2
3
4
5
6
7
8
9
10
11
12
13
四维输入:
 tensor([[[[-0.0766,  0.3599, -0.7820],
          [ 0.0715,  0.6648, -0.2868]],

         [[ 1.6206, -1.5967,  0.4046],
          [ 0.6113,  0.7604, -0.0336]]],


        [[[-0.3448,  0.4937, -0.0776],
          [-1.8054,  0.4851,  0.2052]],

         [[ 0.3384,  1.3528,  0.3736],
          [ 0.0134,  0.7737, -0.1092]]]])

batchnorm

图像数据需要用BatchNorm2d，设置的特征数为channel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# torch自带的batchnorm
torch_bn = nn.BatchNorm2d(num_features=channel, affine=True)  # 注意完整的batchnorm要包括仿射变换

# 仿射变化初始化的weigh=1，bias=0，相当于没有进行变换，看不出效果
# 手动改成别的值，用于对比包含仿射变换的效果
torch.manual_seed(4)  # 设置随机种子，方便复现
torch_bn.weight = nn.Parameter(torch_bn.weight * torch.randn(channel))
torch_bn.bias = nn.Parameter(torch_bn.bias + torch.randn(channel))
print('weight:\n', torch_bn.weight)
print('bias:\n', torch_bn.bias, '\n')

# 结果
torch_normed = torch_bn(inputs)
print('torch bn结果:\n', torch_normed)

仿射变换的参数如下，形状和channel数是一致的，和二维数据的情况一样。这里同样手动给缩放和平移系数加了个随机数

1
2
3
4
5
6
weight:
 Parameter containing:
tensor([-1.6053,  0.2325], requires_grad=True)
bias:
 Parameter containing:
tensor([2.2399, 0.8473], requires_grad=True)

用torch官方batchnorm2d得到的结果是

1
2
3
4
5
6
7
8
9
10
11
12
13
torch bn结果:
 tensor([[[[2.2043, 1.1275, 3.9442],
          [1.8388, 0.3753, 2.7226]],

         [[1.2185, 0.2591, 0.8559],
          [0.9175, 0.9620, 0.7252]]],


        [[[2.8658, 0.7975, 2.2066],
          [6.4684, 0.8186, 1.5090]],

         [[0.8362, 1.1387, 0.8467],
          [0.7392, 0.9660, 0.7027]]]], grad_fn=<NativeBatchNormBackward0>)

再来手动实现一下batchnorm2d

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 手动bn

manual_normed = []
# 每个channel分别处理
for c in range(channel):
    # 计算均值和标准差
    mean = torch.mean(inputs[:, c, :, :])
    std = torch.std(inputs[:, c, :, :], unbiased=False)
    normed = (inputs[:, c, :, :] - mean) / (std + eps) * torch_bn.weight[c] + torch_bn.bias[c]
    normed = normed.unsqueeze(1)
    manual_normed.append(normed)
manual_normed = torch.cat(manual_normed, 1)
print('手动bn结果:\n', manual_normed)

# 手动操作和torch自带操作有点误差，<1e-4
isclose = torch.isclose(torch_normed, manual_normed, rtol=1e-4, atol=1e-4)
print('验证结果:\n', isclose)

如同之前文章所解释，由于CV的卷积计算是通过二维滑动窗口在同一个输入平面上遍历所有位置，因此同一个channel下的多个值对于这个卷积和也是一种"batch"。

相当于对于每一个特征值，计算平均和标准差的范围是N×H×W。

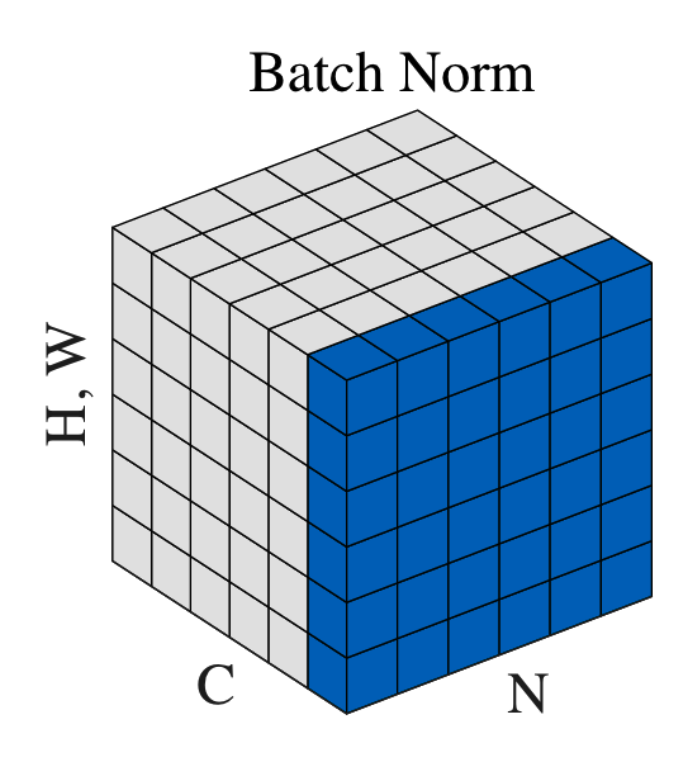
手动计算得到的结果如下，和官方接口一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
手动bn结果:
 tensor([[[[2.2043, 1.1275, 3.9442],
          [1.8388, 0.3752, 2.7226]],

         [[1.2185, 0.2591, 0.8559],
          [0.9175, 0.9620, 0.7252]]],


        [[[2.8658, 0.7975, 2.2066],
          [6.4685, 0.8186, 1.5089]],

         [[0.8362, 1.1387, 0.8467],
          [0.7392, 0.9660, 0.7027]]]], grad_fn=<CatBackward0>)
验证结果:
 tensor([[[[True, True, True],
          [True, True, True]],

         [[True, True, True],
          [True, True, True]]],


        [[[True, True, True],
          [True, True, True]],

         [[True, True, True],
          [True, True, True]]]])

layernorm

按照torch的layernorm官方接口文档，对于图像数据，layernorm是这样做的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# torch自带的layernorm
torch_ln = nn.LayerNorm(
    normalized_shape=[channel, height, width], 
    elementwise_affine=True
)  # 注意完整的layernorm要包括仿射变换

# 仿射变化初始化的weigh=1，bias=0，相当于没有进行变换，看不出效果
# 手动改成别的值，用于对比包含仿射变换的效果
torch.manual_seed(5)  # 设置随机种子，方便复现
torch_ln.weight = nn.Parameter(torch_ln.weight * torch.randn(channel, height, width))
torch_ln.bias = nn.Parameter(torch_ln.bias + torch.randn(channel, height, width))
print('weight:\n', torch_ln.weight)
print('bias:\n', torch_ln.bias, '\n')

# 结果
torch_normed = torch_ln(inputs)
print('torch ln结果:\n', torch_normed)

如同下面这个图所表示

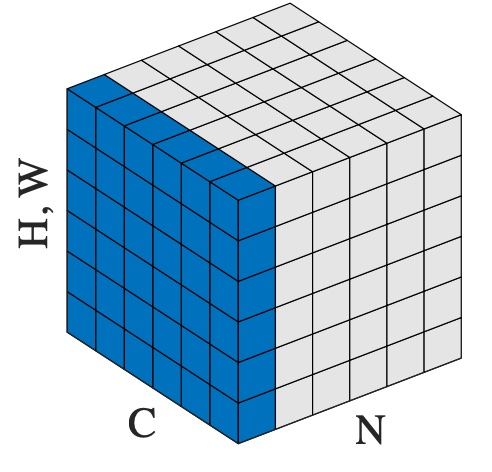
此时仿射变化系数的形状是这样的，为[channel, height, width]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
weight:
 Parameter containing:
tensor([[[-0.4868, -0.6038, -0.5581],
         [ 0.6675, -0.1974,  1.9428]],

        [[-1.4017, -0.7626,  0.6312],
         [-0.8991, -0.5578,  0.6907]]], requires_grad=True)
bias:
 Parameter containing:
tensor([[[ 0.2225, -0.6662,  0.6846],
         [ 0.5740, -0.5829,  0.7679]],

        [[ 0.0571, -1.1894, -0.5659],
         [-0.8327,  0.9014,  0.2116]]], requires_grad=True)

即每个channel内的每一个特征值，都有单独的可训练的仿射变换系数。

layernorm的结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
torch ln结果:
 tensor([[[[ 0.3594, -0.8338,  1.3456],
          [ 0.5128, -0.7147, -0.3012]],

         [[-2.5939,  0.5089, -0.3546],
          [-1.3715,  0.4607,  0.0553]]],


        [[[ 0.5477, -0.9583,  0.8526],
          [-1.2112, -0.6760,  0.9378]],

         [[-0.3219, -2.4580, -0.3647],
          [-0.6744,  0.4171, -0.0264]]]], grad_fn=<NativeLayerNormBackward0>)

手动进行layernorm的归一化和仿射变换，和官方接口对比一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 手动ln

manual_normed = []
# 每个channel分别处理
for b in range(batch_size):
    # 计算均值和标准差
    mean = torch.mean(inputs[b, :, :, :])
    std = torch.std(inputs[b, :, :, :], unbiased=False)
    normed = (inputs[b, :, :, :] - mean) / (std + eps) * torch_ln.weight + torch_ln.bias
    normed = normed.unsqueeze(0)
    manual_normed.append(normed)
manual_normed = torch.cat(manual_normed, 0)
print('手动ln结果:\n', manual_normed)

# 手动操作和torch自带操作有点误差，<1e-4
isclose = torch.isclose(torch_normed, manual_normed, rtol=1e-4, atol=1e-4)
print('验证结果:\n', isclose)

这里计算均值和标准差，是把所有channel内的所有特征值放在一起算的，即每个样本只有一个标量的均值和一个标量的标准差。但是仿射变换的时候就每个特征值都有自己的参数。

手动计算的结果如下，和官方接口一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
手动ln结果:
 tensor([[[[ 0.3594, -0.8338,  1.3456],
          [ 0.5128, -0.7147, -0.3012]],

         [[-2.5939,  0.5090, -0.3546],
          [-1.3715,  0.4607,  0.0553]]],


        [[[ 0.5477, -0.9583,  0.8527],
          [-1.2112, -0.6760,  0.9378]],

         [[-0.3219, -2.4581, -0.3647],
          [-0.6744,  0.4171, -0.0264]]]], grad_fn=<CatBackward0>)
验证结果:
 tensor([[[[True, True, True],
          [True, True, True]],

         [[True, True, True],
          [True, True, True]]],


        [[[True, True, True],
          [True, True, True]],

         [[True, True, True],
          [True, True, True]]]])

NLP数据

再看下在NLP场景下的情况。

先定义输入，N是batch size，S是sequence length，H是hidden size。

1
2
3
4
5
6
7
# 定义一个随机三维输入，[N,S,H]
batch_size = 2
seq_len = 3
hidden_size = 4
torch.manual_seed(6)  # 设置随机种子，方便复现
inputs = torch.randn(batch_size, seq_len, hidden_size)
print('三维输入:\n', inputs)

batchnorm

用官方接口计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# torch自带的batchnorm
torch_bn = nn.BatchNorm1d(num_features=hidden_size, affine=True)  # 注意完整的batchnorm要包括仿射变换

# 仿射变化初始化的weigh=1，bias=0，相当于没有进行变换，看不出效果
# 手动改成别的值，用于对比包含仿射变换的效果
torch.manual_seed(7)  # 设置随机种子，方便复现
torch_bn.weight = nn.Parameter(torch_bn.weight * torch.randn(hidden_size))
torch_bn.bias = nn.Parameter(torch_bn.bias + torch.randn(hidden_size))
print('weight:\n', torch_bn.weight)
print('bias:\n', torch_bn.bias, '\n')

# # 结果
torch_normed = torch_bn(inputs.transpose(1, 2)).transpose(1, 2)
print('torch bn结果:\n', torch_normed)

根据官方接口的描述，输入的第二维应该为特征数，第三维为序列长度，因此这里对输入做了transpose，再把结果transpose回来。

结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
weight:
 Parameter containing:
tensor([-0.1468,  0.7861,  0.9468, -1.1143], requires_grad=True)
bias:
 Parameter containing:
tensor([ 1.6908, -0.8948, -0.3556,  1.2324], requires_grad=True) 

torch bn结果:
 tensor([[[ 1.8740, -0.7037, -1.8222,  2.3385],
         [ 1.7413, -1.8119,  0.3641,  0.0200],
         [ 1.4615, -0.2676,  0.1081,  1.3450]],

        [[ 1.7084, -1.9653,  1.0169,  0.5785],
         [ 1.8213, -0.8614, -0.8056,  2.9892],
         [ 1.5383,  0.2409, -0.9949,  0.1231]]], grad_fn=<TransposeBackward0>)

可以看到batchnorm的仿射变化系数形状在各种情况下都保持和特征向量维度相同。

再来手动计算验证一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 手动bn

# 计算均值
mean = torch.mean(inputs, dim=(0, 1) , keepdim=True)
print('均值:\n', mean)
std = torch.std(inputs, dim=(0, 1), keepdim=True, unbiased=False)
print('标准差:\n', std, '\n')

manual_normed = (inputs - mean) / (std + eps) * torch_bn.weight + torch_bn.bias
print('手动bn结果:\n', manual_normed)

# 手动操作和torch自带操作有点误差，<1e-4
isclose = torch.isclose(torch_normed, manual_normed, rtol=1e-4, atol=1e-4)
print('验证结果:\n', isclose)

这里计算用于归一化均值和方差，是在dim=(0,1)范围内计算的，相当于把[N, S, H]的输入拉平为[N×S, H]的二维输入，再按二维输入的方式进行batchnorm。

结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
均值:
 tensor([[[-0.2151,  0.5444, -0.2633, -0.5424]]])
标准差:
 tensor([[[0.7984, 0.3537, 0.7799, 0.7986]]]) 

手动bn结果:
 tensor([[[ 1.8740, -0.7037, -1.8222,  2.3385],
         [ 1.7413, -1.8119,  0.3641,  0.0200],
         [ 1.4615, -0.2676,  0.1081,  1.3450]],

        [[ 1.7084, -1.9653,  1.0169,  0.5785],
         [ 1.8213, -0.8614, -0.8056,  2.9892],
         [ 1.5383,  0.2409, -0.9950,  0.1231]]], grad_fn=<AddBackward0>)
验证结果:
 tensor([[[True, True, True, True],
         [True, True, True, True],
         [True, True, True, True]],

        [[True, True, True, True],
         [True, True, True, True],
         [True, True, True, True]]])

layernorm

终于来到NLP数据的layernorm，先确认一下，huggingface中bert是这么使用layernorm的

1
2
3
4
5
6
7
8
9
10
11
12
class BertSelfOutput(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.dense = nn.Linear(config.hidden_size, config.hidden_size)
        self.LayerNorm = nn.LayerNorm(config.hidden_size, eps=config.layer_norm_eps)
        self.dropout = nn.Dropout(config.hidden_dropout_prob)

    def forward(self, hidden_states: torch.normTensor, input_tensor: torch.Tensor) -> torch.Tensor:
        hidden_states = self.dense(hidden_states)
        hidden_states = self.dropout(hidden_states)
        hidden_states = self.LayerNorm(hidden_states + input_tensor)
        return hidden_states

用我们的数据跑一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# torch自带的layernorm
torch_ln = nn.LayerNorm(normalized_shape=hidden_size, elementwise_affine=True)  # 注意完整的layernorm要包括仿射变换

# 仿射变化初始化的weigh=1，bias=0，相当于没有进行变换，看不出效果
# 手动改成别的值，用于对比包含仿射变换的效果
torch.manual_seed(8)  # 设置随机种子，方便复现
torch_ln.weight = nn.Parameter(torch_ln.weight * torch.randn(hidden_size))
torch_ln.bias = nn.Parameter(torch_ln.bias + torch.randn(hidden_size))
print('weight:\n', torch_ln.weight)
print('bias:\n', torch_ln.bias, '\n')

# 结果
torch_normed = torch_ln(inputs)
print('torch ln结果:\n', torch_normed)

仿射变化参数的形状和hidden size一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
weight:
 Parameter containing:
tensor([ 0.2713, -1.2729,  0.5027,  0.4181], requires_grad=True)
bias:
 Parameter containing:
tensor([-0.6394, -0.6608, -0.1433, -0.1043], requires_grad=True) 

torch ln结果:
 tensor([[[-0.7547, -2.8528, -0.5092, -0.3423],
         [-1.0957, -0.8780,  0.2388,  0.2097],
         [-0.3502, -1.6158, -0.3133, -0.7224]],

        [[-0.9134, -0.4490,  0.6868, -0.3029],
         [-0.7116, -2.5589, -0.1039, -0.6493],
         [-0.5076, -2.1031, -0.9346, -0.1230]]],
       grad_fn=<NativeLayerNormBackward0>)

再来手动验证一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 手动ln

# 计算均值
mean = torch.mean(inputs, dim=2, keepdim=True)
print('均值:\n', mean)
std = torch.std(inputs, dim=2, keepdim=True, unbiased=False)
print('标准差:\n', std, '\n')

manual_normed = (inputs - mean) / (std + eps) * torch_ln.weight + torch_ln.bias
print('手动ln结果:\n', manual_normed)

# 手动操作和torch自带操作有点误差，<1e-4
isclose = torch.isclose(torch_normed, manual_normed, rtol=1e-4, atol=1e-4)
print('验证结果:\n', isclose)

得到的均值和标准差如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
均值:
 tensor([[[-0.8469],
         [ 0.0745],
         [ 0.3386]],

        [[ 0.1364],
         [-0.7003],
         [ 0.2831]]])
标准差:
 tensor([[[0.8578],
         [0.3354],
         [0.6505]],

        [[0.4426],
         [0.8448],
         [0.6816]]])

每个sample中的每个token，都有各自的均值和标准差，用于归一化。

最终结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
手动ln结果:
 tensor([[[-0.7547, -2.8528, -0.5092, -0.3423],
         [-1.0957, -0.8780,  0.2388,  0.2097],
         [-0.3502, -1.6158, -0.3133, -0.7224]],

        [[-0.9134, -0.4490,  0.6868, -0.3029],
         [-0.7116, -2.5590, -0.1039, -0.6493],
         [-0.5076, -2.1031, -0.9347, -0.1230]]], grad_fn=<AddBackward0>)
验证结果:
 tensor([[[True, True, True, True],
         [True, True, True, True],
         [True, True, True, True]],

        [[True, True, True, True],
         [True, True, True, True],
         [True, True, True, True]]])

归一化的输入能变回原输入吗

既然这些操作是先计算均值和标准差进行归一化，再进行仿射变换，那把仿射变换的参数设置为输入的均值和标准差，是不是就可以把归一化过的数据变回跟原数据一模一样了呢？

以二维情况为例，看下batchnorm是否能变回去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 定义一个随机二维输入
batch_size = 3
feature_num = 4
torch.manual_seed(0)  # 设置随机种子，方便复现
inputs = torch.randn(batch_size, feature_num)
print('二维输入:\n', inputs)

# 计算均值和标准差
mean = torch.mean(inputs, dim=0, keepdim=True)
# print('均值:\n', mean)
std = torch.std(inputs, dim=0, keepdim=True, unbiased=False)
# print('标准差:\n', std, '\n')

# torch自带的batchnorm
torch_bn = nn.BatchNorm1d(num_features=feature_num, affine=True)

# 把仿射变换的缩放和平移替换为标准差和均值
torch_bn.weight = nn.Parameter(std)
torch_bn.bias =  nn.Parameter(mean)
# print('weight:\n', torch_bn.weight)
# print('bias:\n', torch_bn.bias, '\n')

# 结果
torch_normed = torch_bn(inputs)
print('torch bn结果:\n', torch_normed)

isclose = torch.isclose(torch_normed, inputs, rtol=1e-4, atol=1e-4)
print('验证结果:\n', isclose)

结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
二维输入:
 tensor([[ 1.5410, -0.2934, -2.1788,  0.5684],
        [-1.0845, -1.3986,  0.4033,  0.8380],
        [-0.7193, -0.4033, -0.5966,  0.1820]])
torch bn结果:
 tensor([[ 1.5410, -0.2934, -2.1788,  0.5684],
        [-1.0845, -1.3986,  0.4033,  0.8380],
        [-0.7193, -0.4033, -0.5966,  0.1821]],
       grad_fn=<NativeBatchNormBackward0>)
验证结果:
 tensor([[True, True, True, True],
        [True, True, True, True],
        [True, True, True, True]])

确认了batchnorm是可以变回去的。

再来看下layernorm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
print('二维输入:\n', inputs)

# 计算均值和标准差
mean = torch.mean(inputs, dim=1, keepdim=True)
# print('均值:\n', mean)
std = torch.std(inputs, dim=1, keepdim=True, unbiased=False)
# print('标准差:\n', std, '\n')

# torch自带的layernorm
torch_ln = nn.LayerNorm(normalized_shape=feature_num, elementwise_affine=True)  # 注意完整的layernorm要包括仿射变换

# 把仿射变换的缩放和平移替换为标准差和均值
torch_bn.weight = nn.Parameter(std)
torch_bn.bias =  nn.Parameter(mean)
# print('weight:\n', torch_bn.weight)
# print('bias:\n', torch_bn.bias, '\n')

# 结果
torch_normed = torch_ln(inputs)
print('torch ln结果:\n', torch_normed)

isclose = torch.isclose(torch_normed, inputs, rtol=1e-4, atol=1e-4)
print('验证结果:\n', isclose)

结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
二维输入:
 tensor([[ 1.5410, -0.2934, -2.1788,  0.5684],
        [-1.0845, -1.3986,  0.4033,  0.8380],
        [-0.7193, -0.4033, -0.5966,  0.1820]])
torch ln结果:
 tensor([[ 1.1918, -0.1481, -1.5251,  0.4814],
        [-0.8146, -1.1451,  0.7512,  1.2086],
        [-0.9685, -0.0551, -0.6140,  1.6376]],
       grad_fn=<NativeLayerNormBackward0>)
验证结果:
 tensor([[False, False, False, False],
        [False, False, False, False],
        [False, False, False, False]])

发现layernorm并不能通过这种方式把归一化的输入变回原始值，因为layernorm归一化是在特征向量内进行的，所有特征值共享一个均值和方差，但是仿射变换的时候每个特征却有单独的系数。

对于CV数据和NLP数据也有一样的结论。

可以认为batchnorm的归一化和仿射变换是互为可逆的一对操作，而layernorm的归一化和仿射变换是在不同范围内的操作，是不可逆的。

小结

本篇从各种输入数据对batchnorm和layernorm做了手动复现。

需要注意到，batchnorm、layernorm等实际都包含两步操作：①归一化②仿射变换。

基本上，batchnorm可以总结为，对于特征向量中的每一个特征值，在一个"大范围"内进行归一化，这个"大范围"根据输入数据形状，可能是batch，可能是batch×序列长度，或者batch×feature map大小。并且归一化和仿射变换在同一个方向上进行，因此这两个操作是互为可逆的。

而layernorm是在每个特征向量内部进行归一化处理，然后在另一个方向上使用仿射变换。由于归一化和仿射变换的方向不同，因此无法通过把仿射变换，把已经归一化的数据变换为原输入数据。

读到这了，来一发点赞收藏关注吧~

博客：http://www.linsight.cn/
知乎：Linsight
微信公众号：Linsight

【往期文章】

MoE模型的前世今生
LLM长上下文的问题
解锁大模型长上下文能力
理解Attention:从起源到MHA,MQA和GQA
Yi技术报告-划重点看细节
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)

Reference

【1】LAYERNORM https://pytorch.org/docs/stable/generated/torch.nn.LayerNorm.html
【2】BATCHNORM1D https://pytorch.org/docs/stable/generated/torch.nn.BatchNorm1d.html
【3】BATCHNORM2D https://pytorch.org/docs/stable/generated/torch.nn.BatchNorm2d.html