大模型偏好对齐-DPO
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
要对齐大模型偏好并不容易,从预训练的数据内容、模型的结构到SFT数据配比甚至数据格式等都会影响最终结果。
按ChatGPT的技术路线,用SFT+RLHF PPO强化学习确实可以获得一定的提升,但是PPO比较复杂,训练过程不稳定,对微调后的模型、PPO的超参、reward模型的质量等都很敏感,且数据收集和训练的成本都较高,跑通大规模PPO有一定的成本门槛,因此PPO并没有被很广泛地应用。
而DPO,Direct Preference Optimization,就是PPO的一个简化替代方案。DPO不需要训练reward模型,把PPO的两阶段训练变成一阶段训练,让模型可以直接从偏好数据里学习。
DPO公式有点多,但是并不算太复杂,一步一步理解即可。
对齐
大模型在预训练中学到很多知识和技能,但是并不是所有知识和技能都是我们想要的。
比如有一个常见的错误知识,有超过80%的人会有这样的错误认知,那么这个错误知识在预训练数据里也会经常出现。虽然数据集里也会有关于这个知识的正确认知,但是比例相对会比较低。
如果让模型直接用在预训练中学到的知识进行回答,那么模型就有可能给出错误的知识。
这不是我们所希望的。因此需要通过一些方法,让模型给出的结果能对齐人类的偏好,比如最基础的偏好,正确性。
从模型非常广泛的知识和技能中选出我们所需的response和action是构建安全、高效、可控的AI系统的关键。
SFT是最直接的偏好学习方法,而RLHF/RLAIF是上限更高的偏好对齐方案。但RLHF比较复杂,训练不稳定,成本也高。
而DPO的优化目标和RLHF一样,但是实现更简单。
RLHF
先回顾下RLHF的三个阶段。
- SFT Phase
基于预训练模型,在高质量的下游任务数据上训练,获得 \(\pi^{\mathrm{SFT}}\)。
- Reward Modelling Phase
首先给定prompt \(x\),生成两个答案 \((y_1,y_2)\sim\pi^\text{SFT}(y|x)\),并通过人工标注对比 \(y_1,y_2\),获得偏好结果(preference) \(y_w\succ y_l\mid x\),其中w和l表示win和lose。
假设在这些偏好结果中,有一个我们无法直接访问的latent reward model \(r^*(y,x)\),对每对 \((x,y)\) 进行打分,这个 \(r^*(y,x)\) 就是RLHF里reward model的拟合目标。
基于 \(r^*(y,x)\),有很多方法对preference进行建模,Bradley-Terry model就是一个常用的选择。(当然在多个ranked answers的情况下,可以使用Plackett-Luce ranking models)
基于Bradley-Terry model,人类偏好的分布 \(p^{*}\) 写作
\[\begin{aligned}p^*(y_1\succ y_2\mid x)=\frac{\exp\left(r^*(x,y_1)\right)}{\exp\left(r^*(x,y_1)\right)+\exp\left(r^*(x,y_2)\right)}\end{aligned}\]
看起来不复杂,就是把两个答案的reward通过softmax归一化成概率。
假设我们从 \(p^{*}\) 采样到一个静态的偏好对比数据集 \(\mathcal{D}=\left\{x^{(i)},y_w^{(i)},y_l^{(i)}\right\}_{i=1}^N\) ,那我们就可以用基于 \(\pi^{\mathrm{SFT}}\) 初始化得到的reward模型 \(r_\phi(x,y)\),通过maximum likelihood来拟合 \(r^*(y,x)\)。将这个问题表述为二元分类问题,我们就得到negative log-likelihood loss:
\[\mathcal{L}_R(r_\phi,\mathcal{D})=-\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\begin{bmatrix}\log\sigma(r_\phi(x,y_w)-r_\phi(x,y_l))\end{bmatrix}\]
为了确保reward function有较低的方差,一般会对reward进行归一化,使得对于所有的 \(x\),有 \(\mathbb{E}_{x,y\thicksim\mathcal{D}}\left[r_\phi(x,y)\right]=0\)。
- RL Fine-Tuning Phase
在强化学习阶段,我们用上一步中得到的reward给目标模型提供反馈,优化如下目标
\[\max_{\pi_\theta}\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_\theta(y|x)}\begin{bmatrix}r_\phi(x,y)\end{bmatrix}-\beta\mathbb{D}_{\mathrm{KL}}\begin{bmatrix}\pi_\theta(y\mid x)\mid\mid\pi_{\mathrm{ref}}(y\mid x)\end{bmatrix}\]
上式中第一项是reward模型对目标模型(即RLHF中的actor model)给出的答案的reward打分,这一项是越高越好。
而第二项是目标模型和参考模型之间的KL散度,用来限制经过训练后的目标模型,不要偏离参考模型(即 \(\pi^{\mathrm{SFT}}\))太多。这样可以保证reward模型能在经过充分训练的区间工作,同时避免目标模型因过分向高reward分数优化而出现mode-collapse,失去回复的多样性。\(\beta\) 用来控制这个限制项的比重。
由于语言生成是离散的,因此上面这个优化目标是不可导的,需要通过RL优化。
标准的RL把reward fucntion构建成
\[r(x,y)=r_\phi(x,y)-\beta(\log\pi_\theta(y\mid x)-\log\pi_\text{ref}(y\mid x))\]
并通过PPO优化。
Direct Preference Optimization
DPO的目标是推导出一种简单的方法,直接使用偏好来进行policy optimization,而省去训练reward模型的训练。
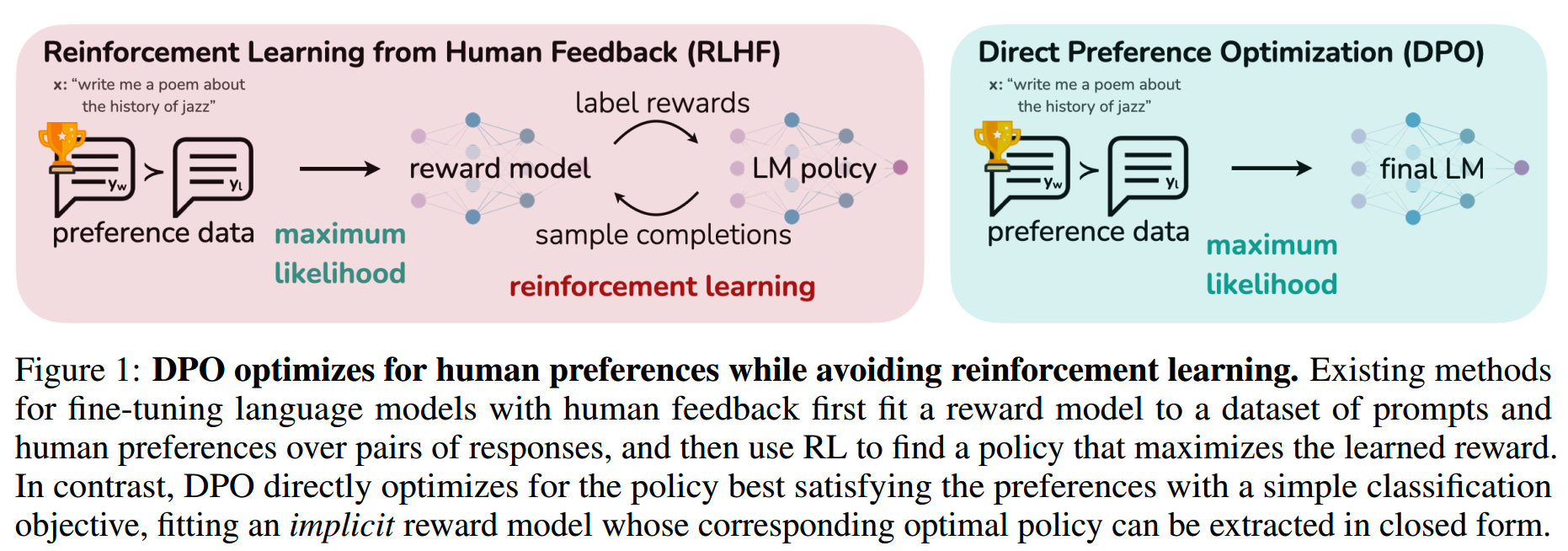
DPO优化目标的推导
首先,DPO起始的优化目标和RL是相同的:对于任意的reward function \(r(x,y)\),reference model \(\pi_{\mathrm{ref}}\)
\[\max_\pi\mathbb{E}_{x\thicksim\mathcal{D},y\thicksim\pi}\begin{bmatrix}r(x,y)\end{bmatrix}-\beta\mathbb{D}_{\mathrm{KL}}\begin{bmatrix}\pi(y|x)||\pi_{\mathrm{ref}}(y|x)\end{bmatrix}\]
由KL散度的定义,把上式中的第二项展开
\[\beta\mathbb{D}_{\mathrm{KL}}(\pi\|\pi_{\mathrm{ref}})=\beta\sum_y\pi(y|x)\log\frac{\pi(y|x)}{\pi_{\mathrm{ref}}(y|x)}\]
这里的条件概率求和其实就是期望值,因此有
\[\max_\pi\mathbb{E}_{x\thicksim\mathcal{D},y\thicksim\pi}\begin{bmatrix}r(x,y)\end{bmatrix}-\beta\mathbb{D}_{\mathbf{KL}}\begin{bmatrix}\pi(y|x)&\mid\mid\pi_{\mathrm{ref}}(y|x)\end{bmatrix}\]
\[\begin{aligned}&=\max_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[r(x,y)-\beta\log\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)}\right]\end{aligned}\]
然后我们把最大化问题转化成最小化问题
\[\begin{aligned}\max_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[r(x,y)-\beta\log\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)}\right]\end{aligned}\]
\[\begin{aligned}&=\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)}-\frac{1}{\beta}r(x,y)\right]\end{aligned}\]
\[\begin{aligned}&=\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)\exp{\left(\frac{1}{\beta}r(x,y)\right)}}\right]\end{aligned}\]
在这里我们用配分函数,归一一下分母。令
\[Z(x)=\sum_y\pi_\text{ref}(y|x)\exp\left(\frac1\beta r(x,y)\right)\]
那我们就得到了一个新的有效的概率分布
\[\begin{aligned}\pi^*(y|x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)\end{aligned}\]
那么就有
\[\begin{aligned}\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)\exp{\left(\frac{1}{\beta}r(x,y)\right)}}\right]\end{aligned}\]
\[\begin{aligned}&=\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)}-\log Z(x)\right]\end{aligned}\]
\[\begin{aligned}&=\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\pi^*(y|x)}-\log Z(x)\right]\end{aligned}\]
由于 \(Z(x)\) 不是 \(y\) 的函数,我们可以把它拿出来
\[\begin{aligned}\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\pi^*(y|x)}-\log Z(x)\right]\end{aligned}\]
\[=\min_\pi\mathbb{E}_{x\thicksim\mathcal{D}}\left[\mathbb{E}_{y\thicksim\pi(y|x)}\left[\log\frac{\pi(y|x)}{\pi^*(y|x)}\right]-\log Z(x)\right]\]
\[=\min_\pi\mathbb{E}_{x\thicksim\mathcal{D}}\left[\mathbb{D}_{\text{KL}}(\pi(y|x)\mid\mid\pi^*(y|x))-\log Z(x)\right]\]
\(Z(x)\) 和 \(\pi\) 无关,因此最小化这个式子只要最小化第一项KL散度。而当且仅当两个分布完全相同的时候,KL散度取得最小值0,因此有
\[\begin{aligned}\pi(y|x)=\pi^*(y|x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)\end{aligned}\]
虽然得到了显示解,但是这里的 \(Z(x)\) 没法求解,因为排列组合数太多,我们不可能去遍历。
继续对这个式子做一些变换
\[\begin{aligned}\pi_r(y|x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)\end{aligned}\]
\[\begin{aligned} \log Z(x)+\log \pi_r(y|x)=\log \pi_{\text{ref}}(y|x) +\frac{1}{\beta}r(x,y) \end{aligned}\]
\[\begin{aligned}r(x,y)=\beta\log\frac{\pi_r(y\mid x)}{\pi_\text{ref}(y\mid x)}+\beta\log Z(x)\end{aligned}\]
这里我们开始用上Bradley-Terry model了。前面我们提到了Bradley-Terry model是如下形式
\[\begin{aligned}p^*(y_1\succ y_2\mid x)=\frac{\exp\left(r^*(x,y_1)\right)}{\exp\left(r^*(x,y_1)\right)+\exp\left(r^*(x,y_2)\right)}\end{aligned}\]
在这个基础上做一点变换
\[\begin{aligned} p^*(y_1\succ y_2\mid x)&=\frac{\exp\left(r^*(x,y_1)\right)}{\exp\left(r^*(x,y_1)\right)+\exp\left(r^*(x,y_2)\right)}\\ &=\frac1{1+\frac{\exp(r^*(x,y_2))}{\exp(r^*(x,y_1))}}\\ &=\frac1{1+\exp(r^*(x,y_2)-r^*(x,y_1))} \end{aligned}\]
然后我们把 \(r\) 代入进去,就得到
\[p^*(y_1\succ y_2\mid x)=\frac{1}{1+\exp\left(\beta\log\frac{\pi^*(y_2|x)}{\pi_{\text{ref}}(y_2|x)}-\beta\log\frac{\pi^*(y_1|x)}{\pi_{\text{ref}}(y_1|x)}\right)}\]
到这里,我们就有了关于optimal policy的人类偏好数据的概率,而无需经过reward模型。我们可以用MLE直接在这个概率模型上优化目标模型
\[\mathcal{L}_{\text{DPO}}(\pi_\theta;\pi_{\text{ref}})=-\mathbb{E}_{(x,y_w,y_l)\thicksim\mathcal{D}}\left[\log\sigma\left(\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_{\text{ref}}(y_w\mid x)}-\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_{\text{ref}}(y_l\mid x)}\right)\right]\]
DPO loss的实现如下

理解DPO损失函数
首先我们了解一下DPO的loss在做什么,对DPO的损失函数求个导。
方便起见,令
\[u=\beta\log\frac{\pi_{\theta}(y_{w}|x)}{\pi_{\mathrm{ref}}(y_{w}|x)}-\beta\log\frac{\pi_{\theta}(y|x)}{\pi_{\mathrm{ref}}(y_{l}|x)}\]
那么原损失函数可以写成
\[L_{DPO}(\pi_{\theta};\pi_{\mathrm{ref}})=-\min_{\pi_{0}}E_{(x,y_{u},y_{t})\sim D}[\log\sigma(u)]\]
对sigmoid求导,有
\[\frac\partial{\partial u}\log\sigma(u)=\frac1{\sigma(u)}\cdot\sigma(u)(1-\sigma(u))=1-\sigma(u)\]
由sigmoid函数性质,有
\[1-\sigma(u)=\sigma(-u)\]
对 \(u\) 求导
\[\frac{\partial u}{\partial\theta}=\beta\left(\frac{\partial}{\partial\theta}\log\frac{\pi_\theta(y_w|x)}{\pi_{\mathrm{ref}}(y_w|x)}-\frac{\partial}{\partial\theta}\log\frac{\pi_\theta(y_l|x)}{\pi_{\mathrm{ref}}(y_l|x)}\right)\]
第一项对数求导,由于 \(\pi_{\mathrm{ref}}\) 不依赖 \(\theta\),可以视作常数,因此有
\[\begin{aligned} \frac\partial{\partial\theta}\log\frac{\pi_\theta(y_w|x)}{\pi_\mathrm{ref}(y_w|x)}=&\frac{1}{\frac{\pi_{\theta}(y_{w}|x)}{\pi_{\mathrm{ref}}(y_{w}|x)}}\cdot\frac{\partial}{\partial\theta}\frac{\pi_{\theta}(y_{w}|x)}{\pi_{\mathrm{ref}}(y_{w}|x)}\\ =&\frac{1}{\pi_{\theta}(y_{w}|x)}\cdot\frac{\partial}{\partial\theta}\pi_{\theta}(y_{w}|x)\\ =&\begin{aligned}\nabla_\theta\log\pi(y_w\mid x)\end{aligned} \end{aligned}\]
类似地,第二项求导
\[\frac{\partial}{\partial\theta}\log\frac{\pi_\theta(y_l|x)}{\pi_{\mathrm{ref}}(y_l|x)}=\nabla_\theta\log\pi(y_l\mid x)\]
因此,DPO损失的导数是
\[\begin{aligned} &\nabla_\theta\mathcal{L}_{\text{DPO}}(\pi_\theta;\pi_{\text{ref}})\\&=-\mathbb{E}_{(x,y_w,y_l)\thicksim\mathcal{D}}\left[\beta\sigma\left(\beta\log\frac{\pi_\theta(y_w|x)}{\pi_{\text{ref}}(y_w|x)}-\beta\log\frac{\pi_\theta(y_l|x)}{\pi_{\text{ref}}(y_l|x)}\right)\left[\nabla_\theta\log\pi(y_w\mid x)–\nabla_\theta\log\pi(y_l\mid x)\right]\right] \end{aligned}\]
再令
\[\hat{r}_\theta(x,y)=\beta\log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)}\]
那么DPO损失的梯度可以写作
\[\begin{aligned} &\nabla_\theta\mathcal{L}_{\text{DPO}}(\pi_\theta;\pi_{\text{ref}})\\&=-\beta\mathbb{E}_{(x,y_w,y_l)\thicksim\mathcal{D}}\left[\sigma\left(\hat{r}_\theta(x,y_l)-\hat{r}_\theta(x,y_w)\right)\left[\nabla_\theta\log\pi(y_w\mid x)–\nabla_\theta\log\pi(y_l\mid x)\right]\right] \end{aligned}\]
梯度各项的意义如下
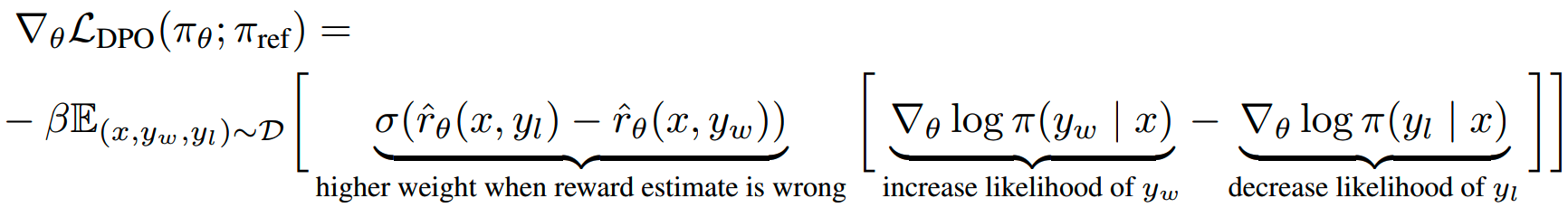
\(\hat{r}_\theta(x,y)\) 相当于 \(\pi_{\theta}\) 和 \(\pi_{\mathrm{ref}}\) 共同确定的隐式reward。
DPO流程
DPO的一般流程是:
- 对于每个prompt \(x\),采样 \(y_1,y_2\sim\pi_{\text{ref}}(\cdot\mid
x)\),然后进行人工标注构建偏好数据集 \(\mathcal{D}=\{x^{(i)},y_w^{(i)},y_l)^{(i)}\}_{i=1}^N\)
- 基于 \(\mathcal{L}_{\mathrm{DPO}}\),在已有的
\(\pi_{\mathrm{ref}}\)、\(\mathcal{D}\) 和 \(\beta\) 上优化 $$
但是收集偏好数据的成本还是比较高的,因此实际使用中,人们更愿意使用开源的偏好数据集。
当我们的偏好数据是来自 \(\pi^{\mathrm{SFT}}\) 的时候,我们直接让 \(\pi_{\mathrm{ref}}=\pi^{\mathrm{SFT}}\)。如果我们使用开源偏好数据集的话,就可能没法直接使用生成这些数据的模型,这时可以用偏好数据集里 \((x,y_w)\) 数据对 \(\pi_{\mathrm{ref}}\) 进行微调,即
\[\pi_{\text{ref}}=\arg\max_\pi\mathbb{E}_{x,y_w\thicksim\mathcal{D}}\left[\log\pi(y_w\mid x)\right]\]
这个微调步骤有助于缓解 \(\pi_{\mathrm{ref}}\) 和真实 reference distribution 之间的distribution shift。
Your Language Model Is Secretly a Reward Model
在前面推导DPO的loss函数的时候,我们把reward的公式显示表达成
\[\begin{aligned}r(x,y)=\beta\log\frac{\pi_r(y\mid x)}{\pi_\text{ref}(y\mid x)}+\beta\log Z(x)\end{aligned}\]
但是这里 \(Z(x)\) 的组合空间太大,实际上没法求解。
好在"在Plackett-Luce/Bradley-Terry模型框架下,同一等价类中的两个reward function有相同的preference distribution"
Under the Plackett-Luce preference framework, and in particular the BradleyTerry framework, two reward functions from the same equivalence class induce the same preference distribution
如果两个reward function \(r(x,y)\) 和 \(r^{\prime}(x,y)\) 可以写成
\[r'(x,y)=r(x,y)+f(x)\]
即表示这两个reward function来自同一等价类(equivalence class)。
对于prompt \(x\) 和 answer \(y_1,\ldots,y_K\),以及对应的ranking \(\tau\),在Plackett-Luce framework(Bradley–Terry也是其中一个特例)下的证明如下
\[\begin{aligned} p_{r'}(\tau|y_1,\ldots,y_K,x)& =\prod_{k=1}^K\frac{\exp(r'(x,y_{\tau(k)}))}{\sum_{j=k}^K\exp(r'(x,y_{\tau(j)}))} \\ &=\prod_{k=1}^K\frac{\exp(r(x,y_{\tau(k)})+f(x))}{\sum_{j=k}^K\exp(r(x,y_{\tau(j)})+f(x))} \\ &=\prod_{k=1}^K\frac{\exp(f(x))\exp(r(x,y_{\tau(k)}))}{\exp(f(x))\sum_{j=k}^K\exp(r(x,y_{\tau(j)}))} \\ &=\prod_{k=1}^K\frac{\exp(r(x,y_{\tau(k)}))}{\sum_{j=k}^K\exp(r(x,y_{\tau(j)}))} \\ &=p_r(\tau|y_1,\ldots,y_K,x) \end{aligned}\]
基于此,我们可以把上面的 \(\beta\log Z(x)\) 项忽略掉,也就是说下面两个reward function是具有相同的preference distribution的
\[\begin{aligned}r(x,y)=\beta\log\frac{\pi_r(y\mid x)}{\pi_\text{ref}(y\mid x)}+\beta\log Z(x)\end{aligned}\]
\[\hat{r}_\theta(x,y)=\beta\log\frac{\pi_\theta(y|x)}{\pi_\text{ref}(y|x)}\]
更进一步地,两个来自同一等价类的reward function在相同的RL问题下会导向相同的optimal policy。
在推导DPO的loss的部分中,我们得到了optimal policy的显式解
\[\begin{aligned}\pi(y|x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)\end{aligned}\]
这里证明一下两个reward function可以导向相同的optimal policy。假设\(r'(x,y)=r(x,y)+f(x)\),\(\pi_r\) 和 \(\pi_{r'}\) 分别是它们对应的optimal policy,有
\[\begin{aligned} \pi_{r^{\prime}}(y|x)& \begin{aligned}&=\frac{1}{\sum_y\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r'(x,y)\right)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r'(x,y)\right)\end{aligned} \\ &=\frac{1}{\sum_y\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}(r(x,y)+f(x))\right)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}(r(x,y)+f(x))\right) \\ &\begin{aligned}=\frac{1}{\exp\left(\frac{1}{\beta}f(x)\right)\sum_y\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)\exp\left(\frac{1}{\beta}f(x)\right)\end{aligned} \\ &\begin{aligned}&=\frac{1}{\sum_y\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)}\pi_{\text{ref}}(y|x)\exp\left(\frac{1}{\beta}r(x,y)\right)\end{aligned} \\ &=\pi_r(y|x) \end{aligned}\]
那么,与Plackett-Luce(特别是Bradley-Terry)模型一致的所有reward类别,都可以被某个模型 \(\pi(y\mid x)\) 和 一个给定的reference model \(\pi_{ref}(y\mid x)\) 所表示:
\[r(x,y)=\beta\log\frac{\pi(y|x)}{\pi_{ref}(y|x)}\]
也就是我们的语言模型都天然具有reward model的功能。
实验
实际训练中,论文中所使用的超参和设置:
- \(\beta=0.1\)(对于TL;DR
summarization,设为0.5)
- batch size = 64
- RMSprop optimizer
- learning rate = 1e-6
- linearly warmup 0 to 1e-6 over 150 steps
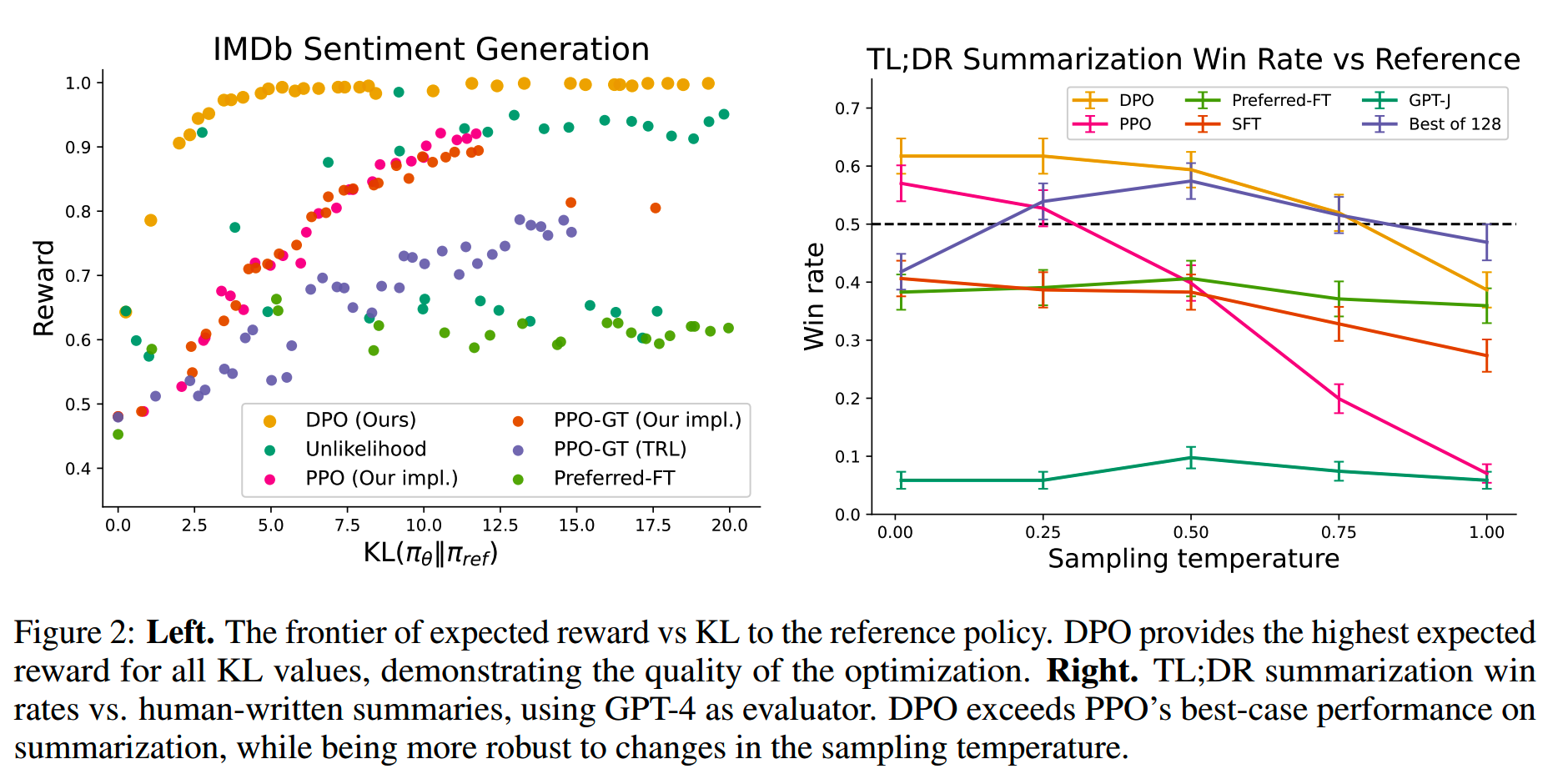
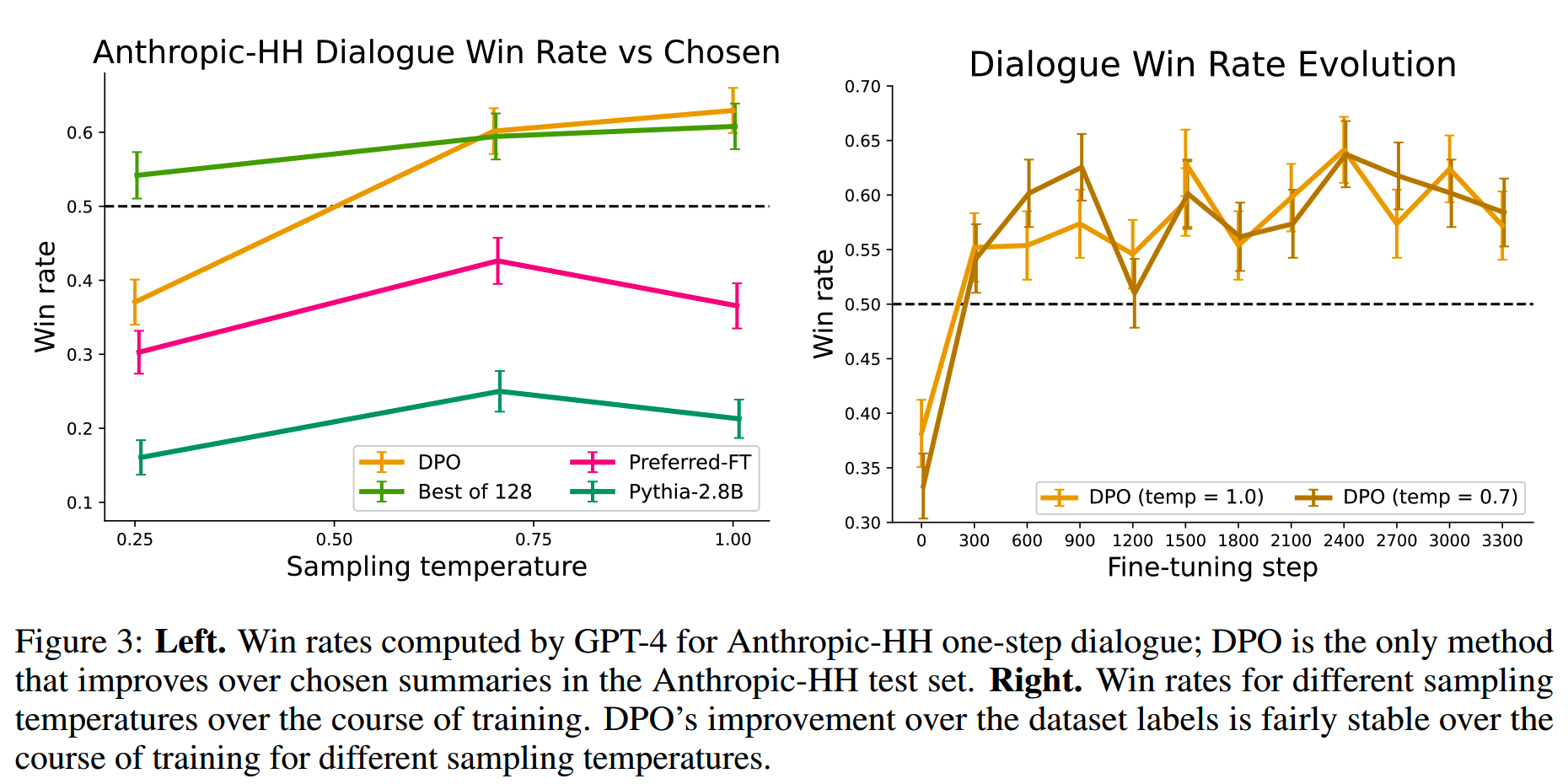
论文在对话、摘要等任务进行的效果评测,主要对比了PPO、SFT和DPO的效果。
DPO即使在没有精细调参的情况下,也有比价好的效果
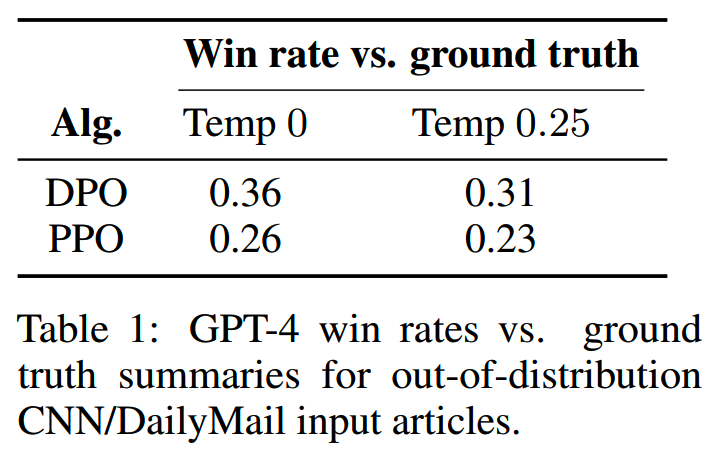
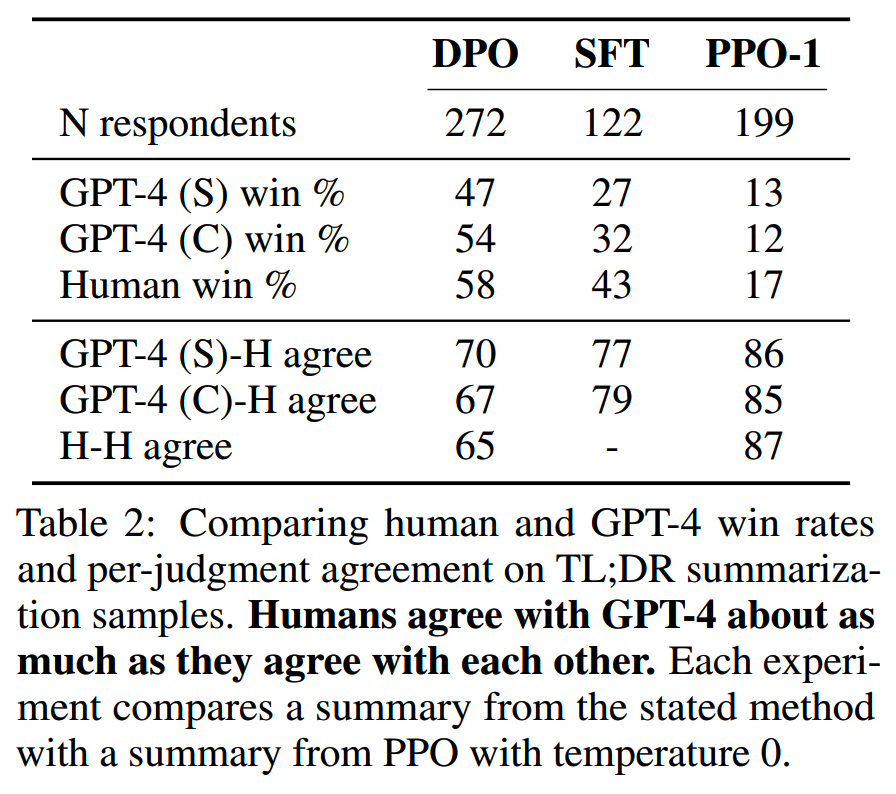
小结
- DPO在RLHF
PPO相同的优化问题下,推导出了新的优化形式,省去了reward模型的部分,从而可以直接用偏好数据优化模型
- DPO在效果和效率上相比PPO都有优势
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

【往期文章】
MoE模型的前世今生
LLM长上下文的问题
解锁大模型长上下文能力
大模型推理窗口-从有限到无限大
理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
Yi技术报告-划重点看细节
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding
window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)
Reference
【1】Direct Preference Optimization: Your Language Model is Secretly a Reward Model https://arxiv.org/abs/2305.18290v2