大模型偏好对齐-simPO
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
前面我们对DPO和ODPO的思路做了整理:大模型偏好对齐-DPO,大模型偏好对齐-ODPO。
最近新出的simPO受到了很多关注。相比DPO,simPO不需要reference model,并且有更好的效果。simPO的另一个好处是,能够保持生成结果在较短长度下的质量。
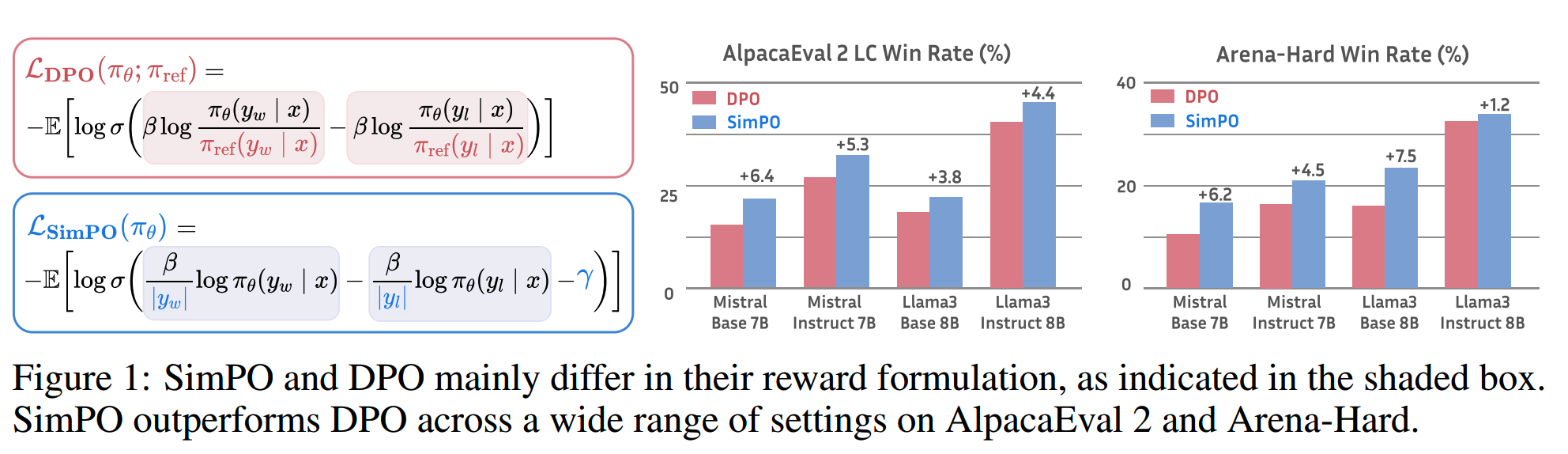
DPO的局限
回顾一下DPO。DPO的reward function有一个closed-form expression
\[\begin{aligned}r(x,y)=\beta\log\frac{\pi_\theta(y\mid x)}{\pi_\text{ref}(y\mid x)}+\beta\log Z(x)\end{aligned}\]
基于此,通过Bradley-Terry model进行建模,得到损失函数
\[\mathcal{L}_{\text{DPO}}(\pi_\theta;\pi_{\text{ref}})=-\mathbb{E}_{(x,y_w,y_l)\thicksim\mathcal{D}}\left[\log\sigma\left(\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_{\text{ref}}(y_w\mid x)}-\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_{\text{ref}}(y_l\mid x)}\right)\right]\]
理论上,DPO的优化目标和RLHF是一致的,但是DPO有两个缺陷:
- 仍然需要一个reference model,这样依然有比较大的内存和计算开销
-
训练过程中优化的reward和推理时的生成指标存在差异,也就是训练和推理的目标不完全对齐
第二点怎么理解呢?模型在自回归生成response时,理论上是寻找最大化所有token平均log likelihood的组合,即
\[\begin{aligned}p_\theta(y\mid x)=\frac{1}{|y|}\log\pi_\theta(y\mid x)=\frac{1}{|y|}\sum_{i=1}^{|y|}\log\pi_\theta(y_i\mid x,y_{<i})\end{aligned}\]
当然实际上这个组合空间太大了,没法直接遍历寻找,因此会使用一些解码策略来寻找局部最优解,比如greedy decoding、beam search或者top-k sampling等,不过我们还是可以按这个公式近似计算。另外这个公式还是可用在多个response/多选题的排序上的。
可以看到推理时的这个目标和DPO的reward差了个referenc model。那么在DPO里,满足 \(r(x,y_w)>r(x,y_l)\) 的偏好数据并不一定意味着 \(p_\theta(y_w\mid x)>p_\theta(y_l\mid x)\)。
论文做了一个统计,对于DPO,满足 \(r(x,y_w)>r(x,y_l)\) 和 \(p_\theta(y_w\mid x)>p_\theta(y_l\mid x)\) 两个结果对齐的比例大概只有50%,如下图所示
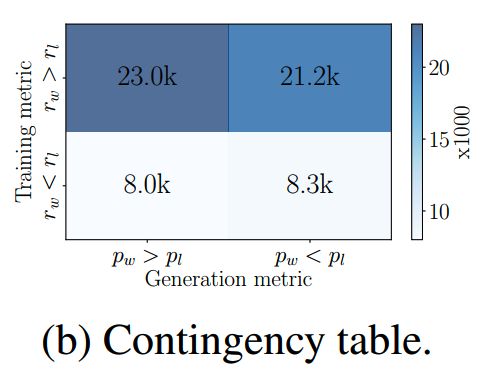
这就是训练和推理目标没有完全对齐。
而simPO则可以完全对齐
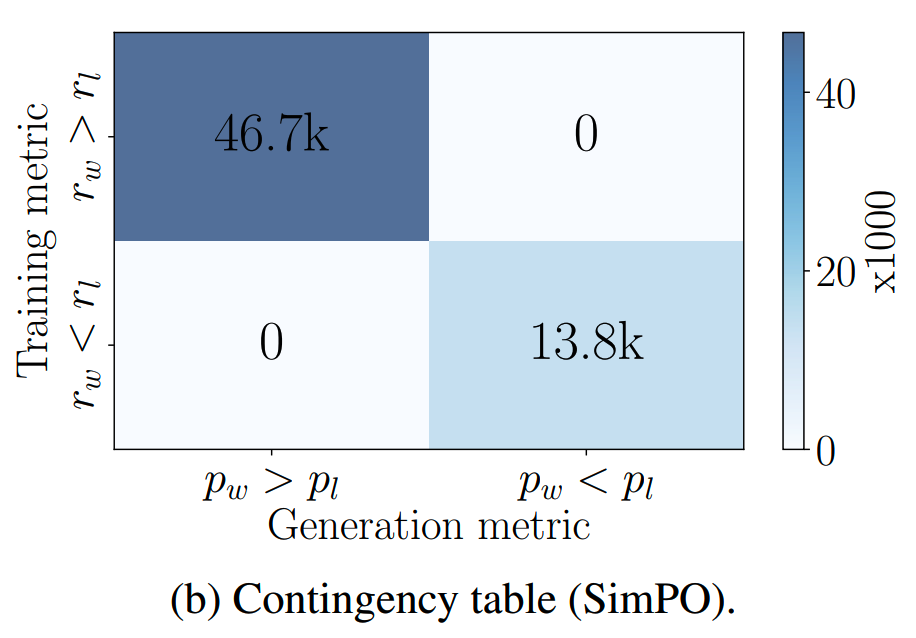
simPO
损失函数
从上面这个分析,我们自然就想到要把训练的目标往推理目标上靠拢对齐。那么最直接的做法,就是把reward从
\[\begin{aligned}r^*(x,y)=\beta\log\frac{\pi_\theta(y\mid x)}{\pi_\text{ref}(y\mid x)}\end{aligned}\]
(这里省略了配分函数Z)
变成
\[\begin{aligned}r_{\text{SimPO}}(x,y)=\frac{\beta}{|y|}\log\pi_\theta(y\mid x)=\frac{\beta}{|y|}\sum_{i=1}^{|y|}\log\pi_\theta(y_i\mid x,y_{<i})\end{aligned}\]
注意这里有个长度归一化项,这个很重要,没有这一项的话,模型会倾向于生成长度更长但是低质量的内容。
除了修改reward的计算,simPO和IPO、ODPO一样,引入了一个reward margin,这是一个固定的超参,要求winning response和losing response的reward差值要大于reward margin
\[p(y_w\succ y_l\mid x)=\sigma\left(r(x,y_w)-r(x,y_l)-\gamma\right)\]
按已有的经验,增大这个margin有助于提高模型泛化能力,但是太大的margin也会导致模型的退化。
至此我们得到了simPO的损失函数
\[\mathcal{L}_{\text{SimPO}}(\pi_\theta)=-\mathbb{E}_{(x,y_w,y_l)\thicksim\mathcal{D}}\left[\log\sigma\left(\frac{\beta}{|y_w|}\log\pi_\theta(y_w|x)-\frac{\beta}{|y_l|}\log\pi_\theta(y_l|x)-\gamma\right)\right]\]
simPO梯度更新的直观理解
DPO和simPO的梯度如下
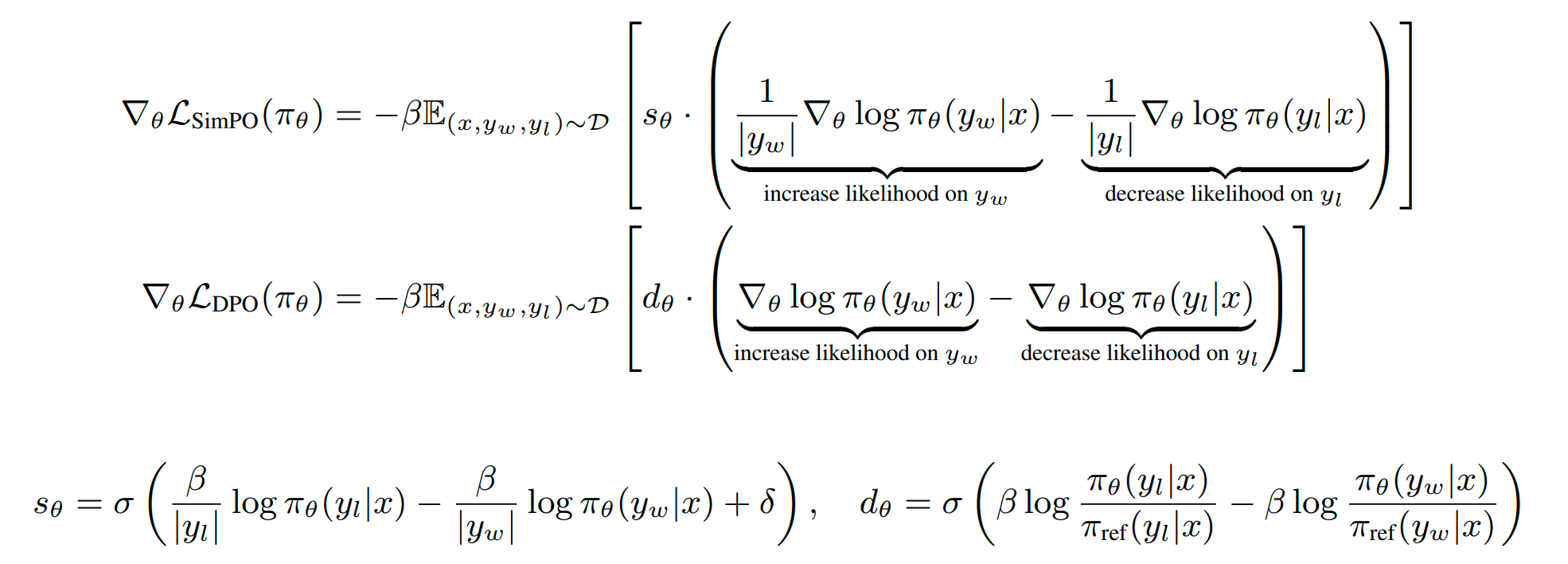
DPO和simPO的梯度有两个主要区别:
- 梯度权重:simPO的梯度权重没有包含reference model,这样当policy
model给dispreferred
response更高的reward的时候,权重就会变大,加强对这个错误case的修正力度。
- simPO的梯度更新带有length-normalized;而如《Disentangling length from
quality in direct preference
optimization》所发现,DPO里更长的token会有更大的梯度值从而主导了梯度更新的过程,这导致训练出来的模型倾向于生成更长的模型。
实验
设置
论文使用了Llama3-8B和Mistral-7B的base和instruct模型进行实验。
对于base模型,就先在UltraChat-200k数据集上训练一个对应的SFT模型,之后在 UltraFeedback数据集上进行preference optimization。
对于instruct模型,参照《Iterative DPO alignment》的做法,先用这些SFT模型生成preference数据集。具体来说,使用UltraFeedback的prompt,用temperature=0.8的配置,从SFT模型生成5个response,并用PairRM(《LLM-Blender: Ensembling large language models with pairwise ranking and generative fusion》)对这5个response进行打分,选择最高分作为preferred response,最低分的座位dispreferred response。
这样就得到了四组实验组合:Llama3-Base, Llama3-Instruct, Mistral-Base和Mistral-Instruct。
此外,论文发现超参对preference optimization的影响很大,因此对不同的方法进行了超参搜索,范围如下
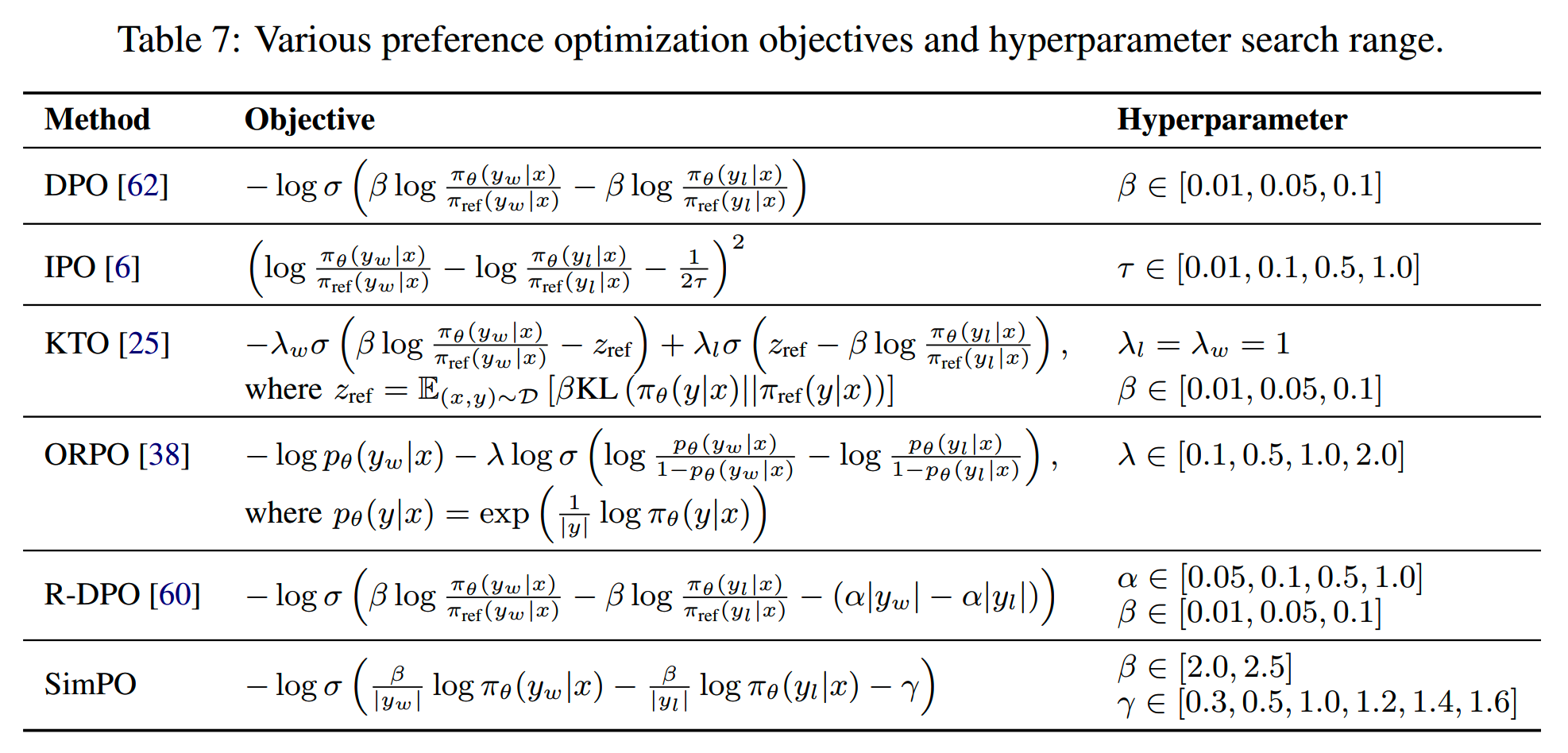
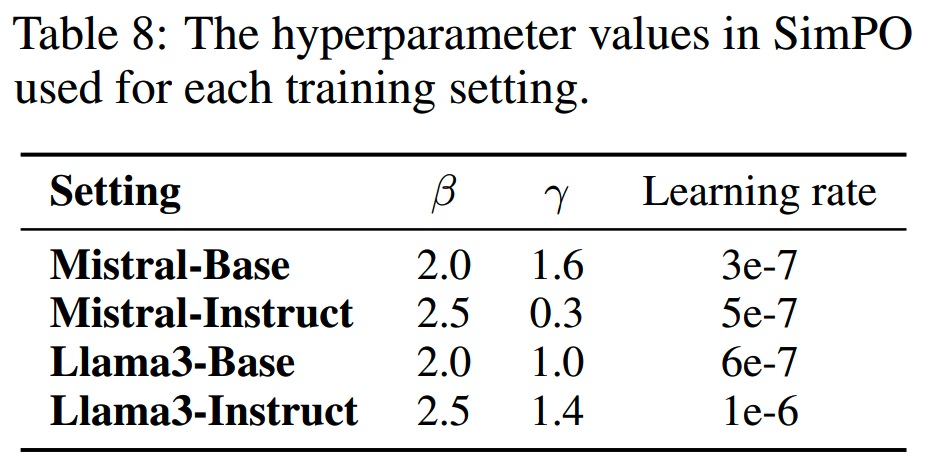
此外对batch size、解码温度等参数也进行搜索。
所用的数据集如下

对比
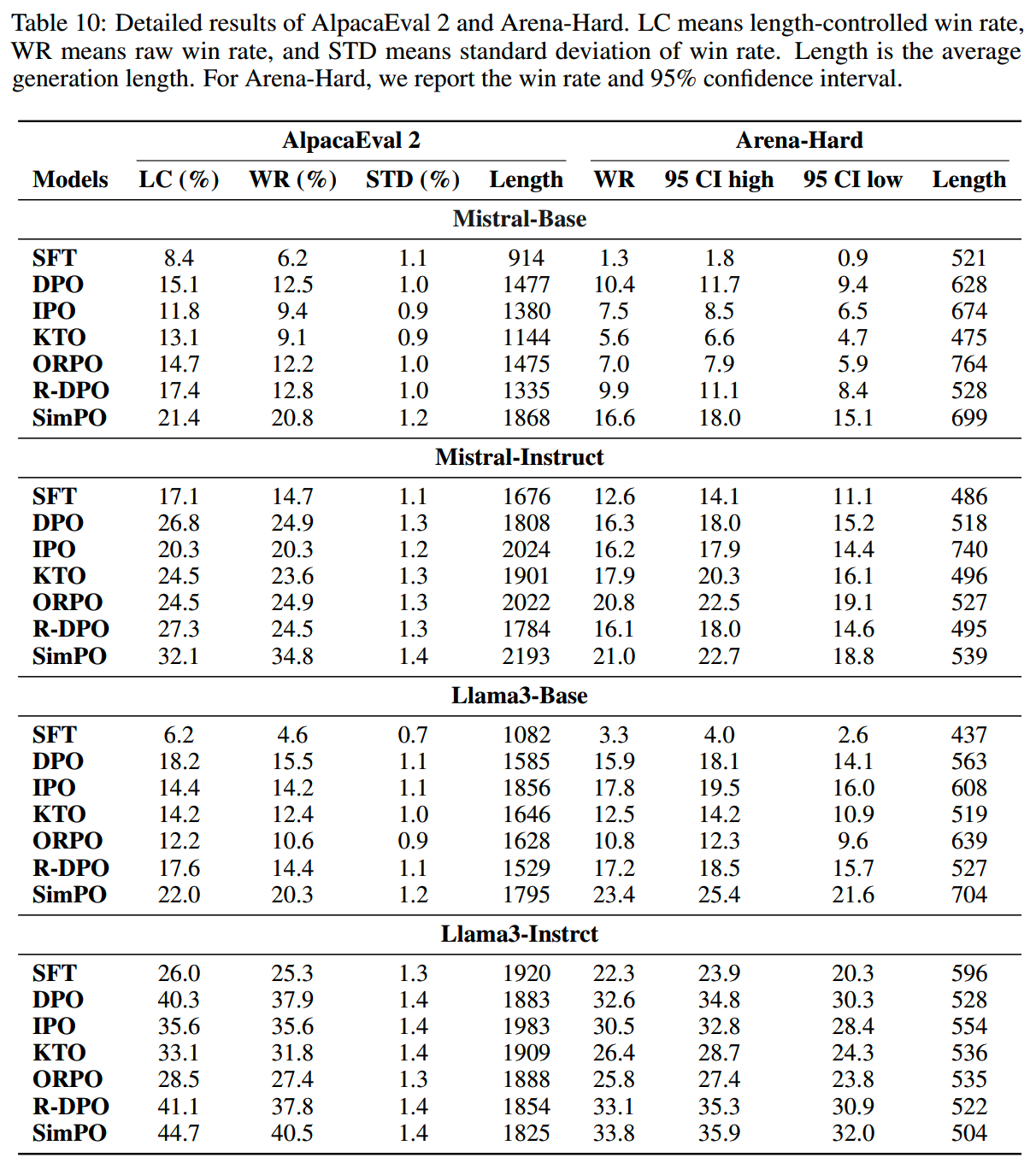
在各个数据集上,不同的优化方法结果对比如下
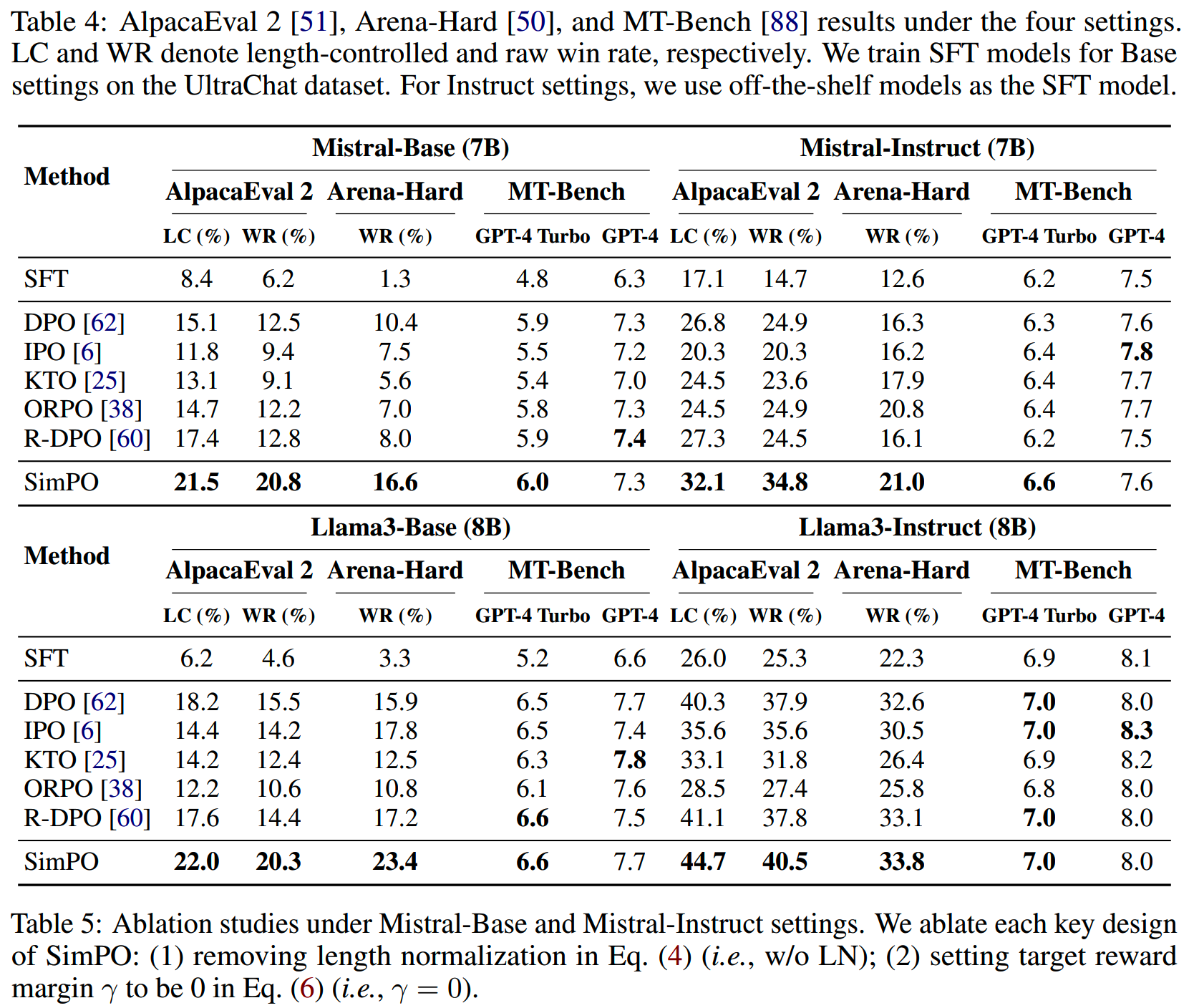
其中LC表示length-controlled,即在限制长度条件下的win rate。
有几个发现:
-
在MT-Bench上,各个方法的差异不大,那些微小的波动可能更多来自于随机性。究其原因可能是因为这个数据集的量比较少,且评价的方案也比较单一,这个发现和《From
live data to high-quality benchmarks: The Arena-Hard
pipeline》的发现是一致的。
-
instruct模型的表现比base要好,这可能是因为这些精心微调过甚至强化学习过的模型本身质量更高。
- 在AlpacaEval 2和Arena-Hard上,simPO在raw win rate和length-controlled
win rate相比其他方案都有明显优势。
消融实验
simPO两个主要的部分就是length normalization和margin。分别去掉这两个部分之后的结果如下表
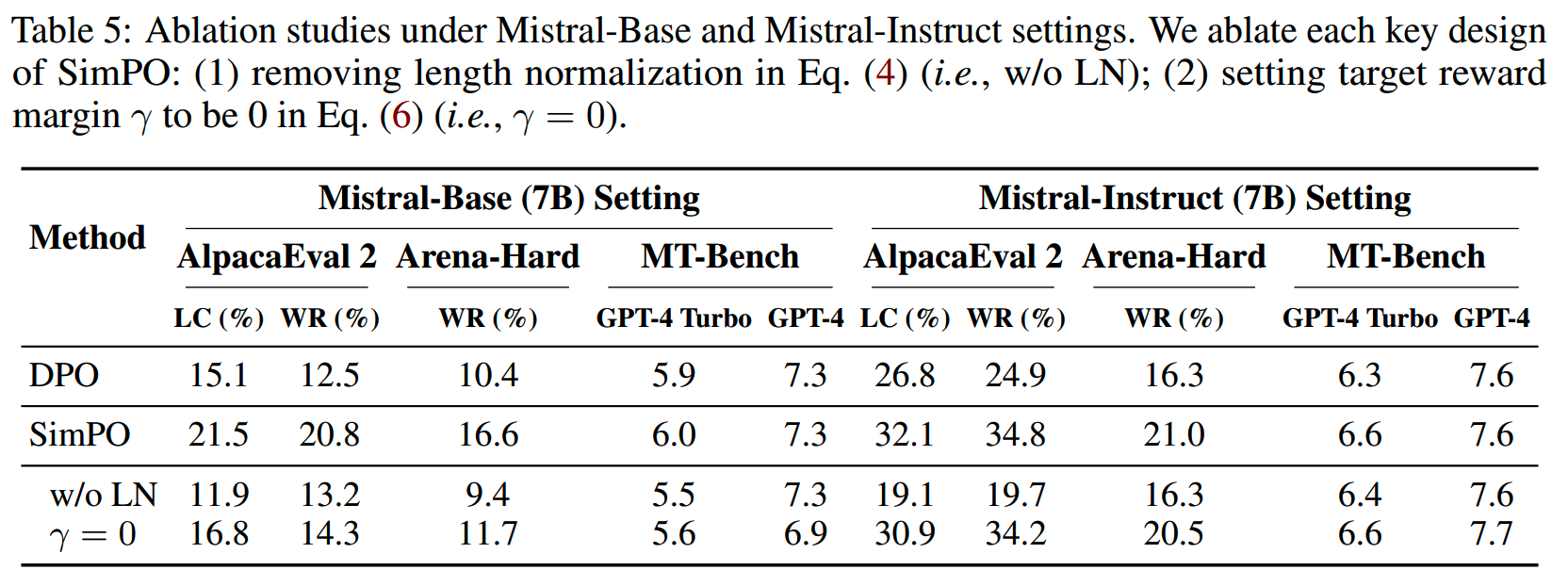
结果上看,length normalization的影响很大,margin也有一定的影响。
下面具体分析一下。
首先是关于长度归一化。从上表的结果上看,对于simPO,使用长度归一化会让模型生成更短且质量更高的结果。
对比其他训练方法,simPO在长度控制下的win rate有明显优势,这说明simPO实现了对生成长度的最小利用,即不通过长篇大论来提高得分。
而通用来说,生成结果的长度和质量之间并没有什么强联系。如下表所示,各个训练方法的生成长度和wr并没有什么明显规律,这表明,生成结果的长度并不是衡量生成质量的一个可靠指标。
此外,长度归一化会增大偏好数据对之间的reward差。这个很好理解,在有长度归一化的损失函数下,想要达到相同的reward差,模型需要给出y倍的数值才能比margin大。
论文把在不同的长度差异下的reward差画出来,如下图所示
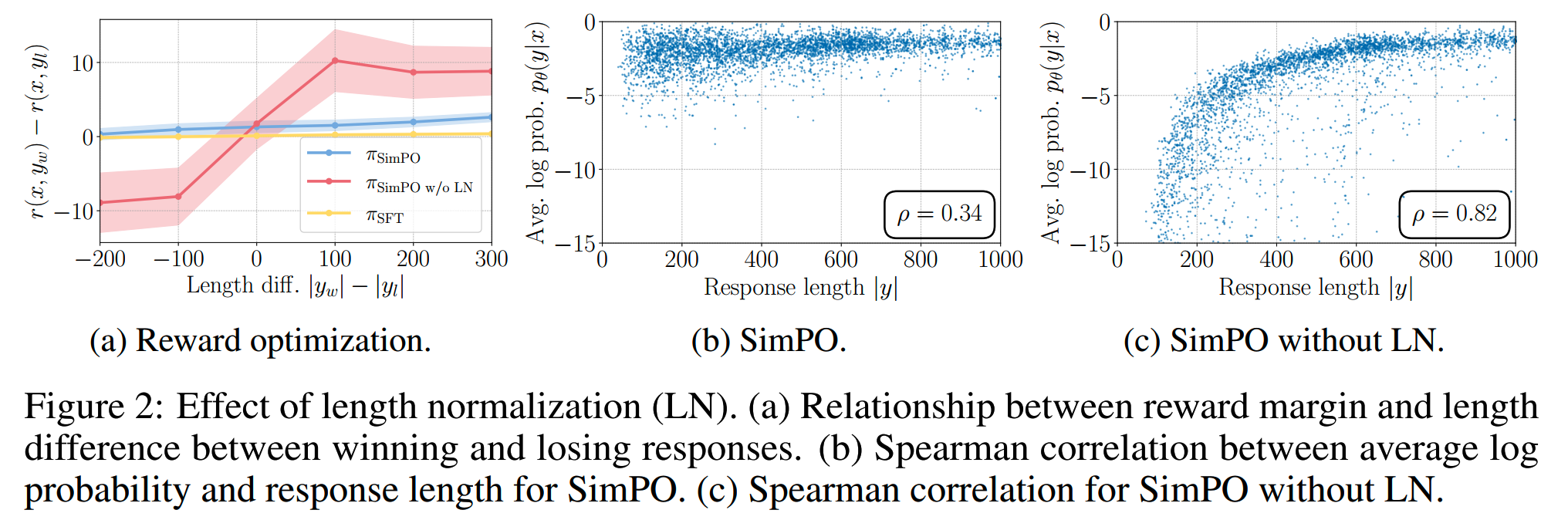
可以发现带有长度归一化的simPO无论数据的长度差如何,都能给出positive reward margin,而没有带长度归一化的模型在winning response的长度更短的情况下,会给出negative reward difference,这表明模型对这些样本的学习效果很差。
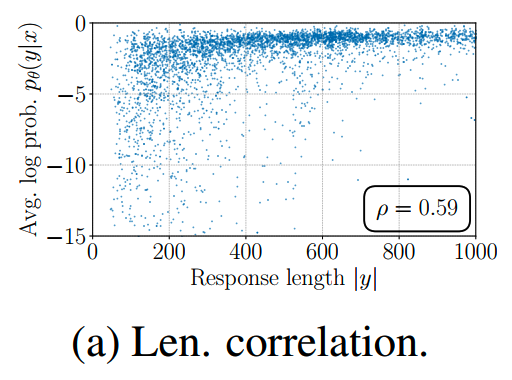
而从上图b和c子图可以看出,移除长度归一化会使得reward和response length呈现强烈的正相关关系,而这显然不是我们想要的。
接下来看下reward margin的影响。
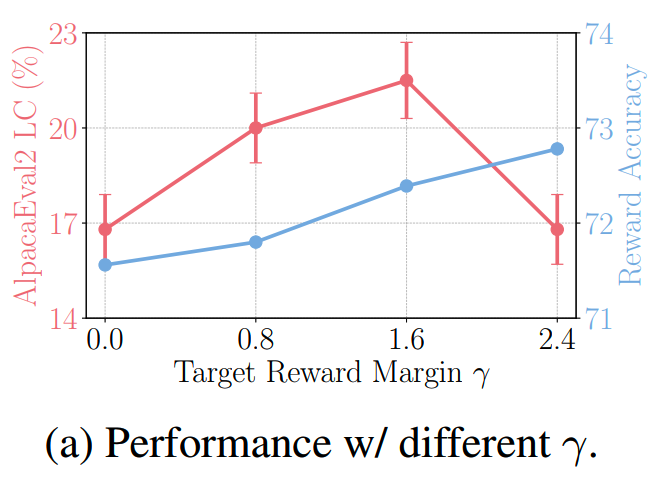
把reward accuracy定义为policy model对winning response的reward高于losing response的比例。那么如下图所示,随着margin的增大,reward accuracy也在提升
另外实验还发现,增大reward margin,会使得reward difference和winning response的平均对数似然的分布变得扁平,且winning response的平均对数似然会减小,如下图所示
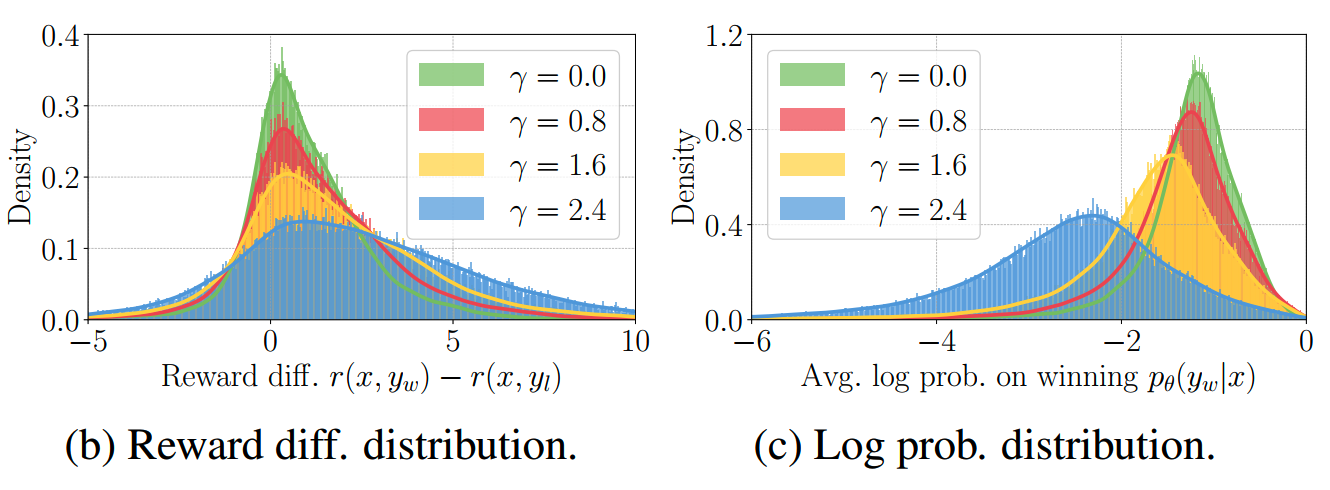
这说明太大的margin设置对模型会有负面影响,因此需要寻找一个中间值使得模型效果最好。
DPO和simPO的对比
- 虽然DPO的reward表达式里没有显式涵盖长度归一化的信息,但是由于使用了reference model进行对比,在一定程度上可以对抗length bias。如下图所示,DPO在一定程度上可以打破长度和reward之间的正相关关系,但是没有simPO的效果那么好
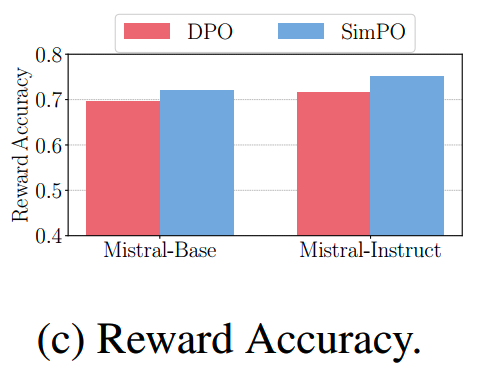
- simPO比DPO有更高的reward accuracy,这表明simPO的reward设计有更强的泛化能力,可以提供更高质量的生成能力
小结
simPO对损失函数做了一些改变,对齐了训练和推理的目标,使得policy model能够在提升效果的同时,不过分影响生成结果的长度。并且simPO不再需要reference model,这也使得训练的空间成本更加节省。
论文在LLAMA和Mistral两个热门的模型上进行了比较多的实验,比较有说服力。
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

【往期文章】
MoE模型的前世今生
LLM长上下文的问题
解锁大模型长上下文能力
大模型推理窗口-从有限到无限大
理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
大模型偏好对齐-DPO
大模型偏好对齐-ODPO
Yi技术报告-划重点看细节
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding
window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)
Reference
【1】SimPO: Simple Preference Optimization with a Reference-Free Reward https://arxiv.org/abs/2405.14734