MoE的top-p routing
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
北大、快手和AGIBang共同提出MoE模型的dynamic routing机制,把gating的top-k routing改成top-p routing,在减少平均激活参数量的同时效果还略有提升。
MoE相关基础可参考MoE模型的前世今生。
routing
top-k routing
目前大部分的MoE模型采用的routing策略是top-k routing。比如当 k = 2,则每个输入token在每个MoE层会激活2个专家(忽略token drop等机制)。
假设每个MoE层有N个expert,这些expert的集合记为 \(E=\{e_{1},e_{2},..,e_{N}\}\),那么输入token x在MoE层的计算如下:
\[MoE(\mathbf{x})=\sum_{i=1}^Ng_i(\mathbf{x})*e_i(\mathbf{x})\]
\[g_i(\mathbf{x})=\begin{cases}\frac{P_i}{\sum_{j\in TopK(\mathbf{P})}P_j},&i\in TopK(\mathbf{P})\\0,&i\notin TopK(\mathbf{P})\end{cases}\]
\[\mathbf{P}=Softmax(\mathbf{W_r}\cdot\mathbf{x}^T)\]
top-k routing由Google在《Outrageously large neural networks: The sparsely-gated mixture-of-experts layer》中提出,应用在LSTM模型上,之后的一些工作比如《Gshard》、《Switch Transformer》、《ST-MoE》和《Taming sparsely activated transformer with stochastic experts》等则引入了相关constraint来确保多个专家间的负载均衡,以保障模型的效果和效率。
top-p routing
虽然top-k routing的效果不错,但是每个token都激活相同数量的专家这个假设粗暴地忽略了不同输入token之间的难度区别,并且在不同MoE层也都激活相同数量的专家这样的策略也没有考虑到模型不同层间的表达能力差异。
针对这个情况,就有了top-p routing的策略:不直接限制每个token激活的专家数量,而是根据设定的阈值p(超参),一个一个把候选专家中gating得分最高的加入到激活专家集合里,直到激活专家集合的accumulative confidence超过p。写成公式如下:
\[t=\underset{k\in\{1...,N\}}{argmin}\sum_{j<=k}P_{i,j}\geq p\]
\[g_i(\mathbf{x})=\begin{cases}P_i&e_i\in S\\0,&e_i\notin S\end{cases}\]
\[S=\{e_{I_1},e_{I_2}...e_{I_t}\}\]
top-k routing和top-p routing的示意图如下:
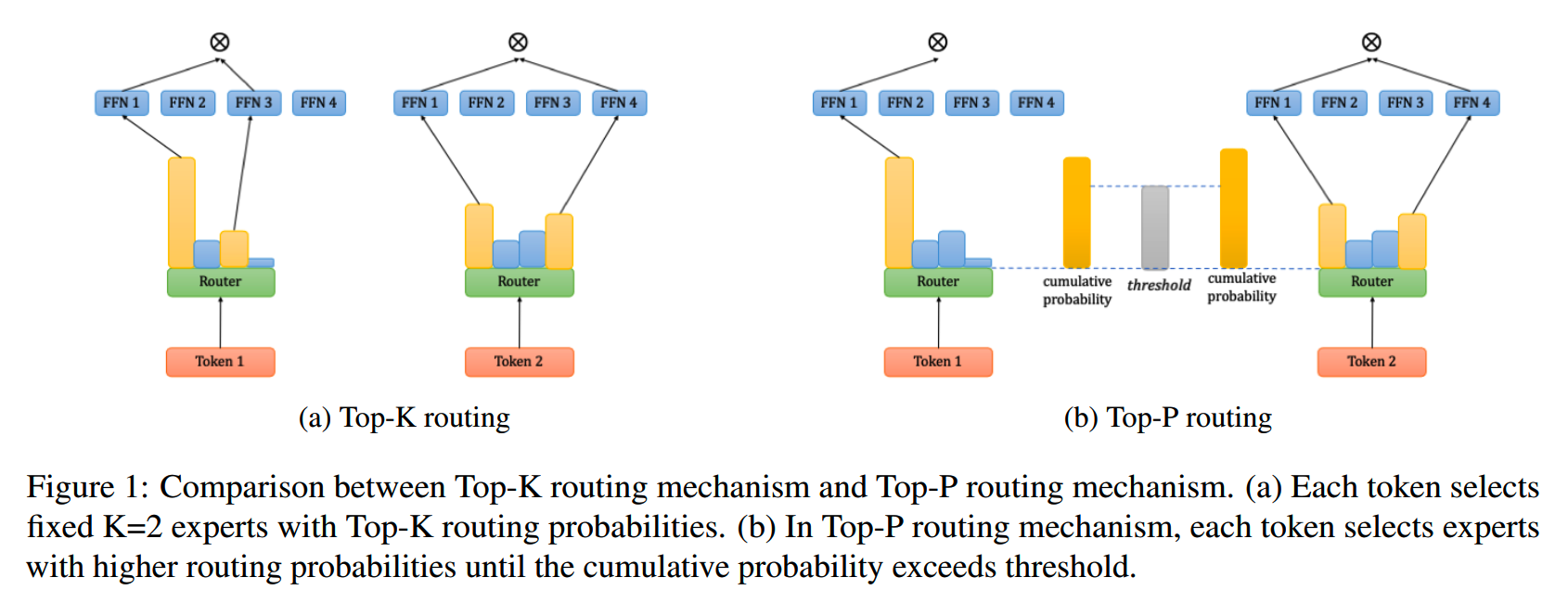
Loss
Dynamic Loss
使用top-p routing会有一个风险:模型可能会学到把gating的权重在所有专家间进行均匀分配的策略,因为这样可以使得激活的专家数最大。
比如阈值p设置为0.5,那么在所有专家的权重均匀分配的情况下,激活专家数为总专家数的一半,这远多于正常MoE机制下的激活比例。这样由于激活参数量较大,最终模型的效果就会更好。
但这样的均匀分配策略显然是违背了MoE设计的初衷的。
为了避免这个问题,避免出现均匀分布的情况,可以增加一个dynamic loss,要求模型最小化权重分布P的熵,让不同专家可以专注在特定的领域,提高专家化的程度:
\[Loss_d=-\sum_{i=1}^NP_i*log(P_i)\]
Load Balance Loss
这里负载均衡损失的设计就比较常规,和很多其他MoE模型所用的一致:
\[Loss_b=N*\sum_{i=1}^Nf_i*Q_i\]
\[f_i=\frac{1}{M}\sum_{j=1}^M1\{e_i\in S^j\}\]
\[Q_i=\frac{1}{M}\sum_{j=1}^nP_i^j\]
\(S^{j}\) 是第j个token激活的专家集合。
Final Loss
最后完整的训练loss计算如下:
\[Loss=Loss_{lm}+\alpha Loss_b+\beta Loss_d\]
训练中,使用了 \(\alpha=1e-2\),\(\beta=1e-4\)。
实验
数据
从RedPajama抽了100B数据,包括common crawl (CC), C4, github, Wikipedia, books, arxiv 和 Stackexchange。
模型
模型采用LLaMA的结构:
- vocab size = 32000
- layer num = 24
- 初始化standard deviation = 0.006
- MHA,head num = 16,head size = 64
共设计了5个模型:
- dense模型1:hidden size = 1024,总参数量 = 374M
- dense模型2:hidden size = 1280,总参数量 = 570M
- top-1 MoE模型:hidden size = 1024,专家数 = 16,总参数量 =
3.5B,激活参数量 = 374M
- top-2 MoE模型:hidden size = 1024,专家数 = 16,总参数量 =
3.5B,激活参数量 = 581M
- top-p MoE模型:hidden size = 1024,专家数 = 16,总参数量 = 3.5B,阈值p
= 0.4
训练设置如下:
- AdamW,beta_1 = 0.9, beta_2 = 0.95
- weight decay = 0.1
- cosine schedule
- max lr = 3e-4,final lr = 3e-5
- warmup = 2000 step
- context length = 2048
- batch size = 2048
上面5个模型的在下游任务的对比如下
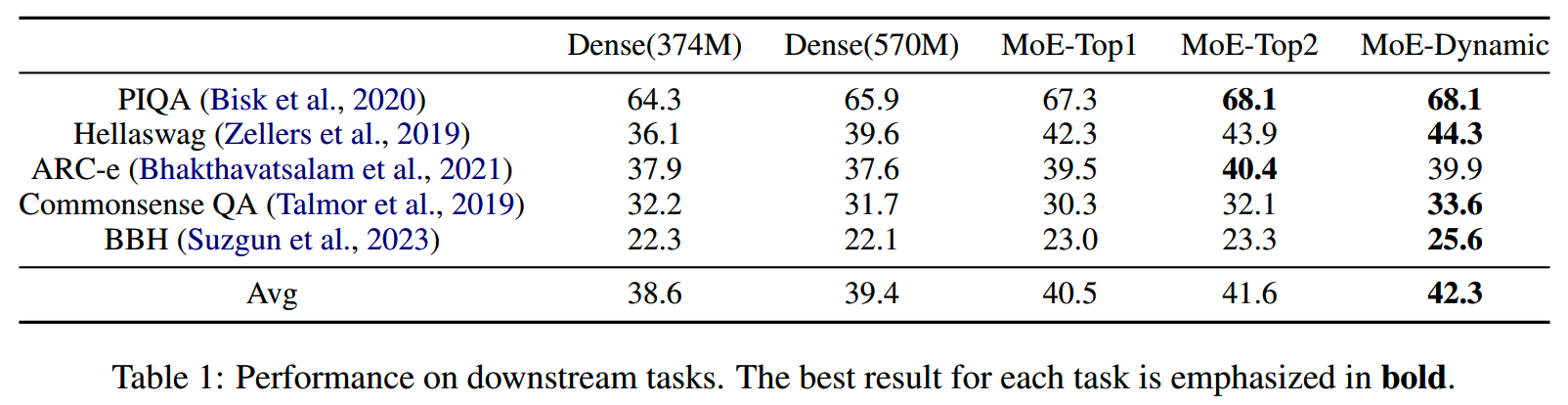
top-p MoE在下游任务上的平均激活专家数为1.76。
top-p MoE以≤top-2 MoE模型90%的激活参数量,获得了比top-2 MoE提升0.7%的效果。
分析
p的影响
不同的阈值p(0.1~0.7)下的模型效果
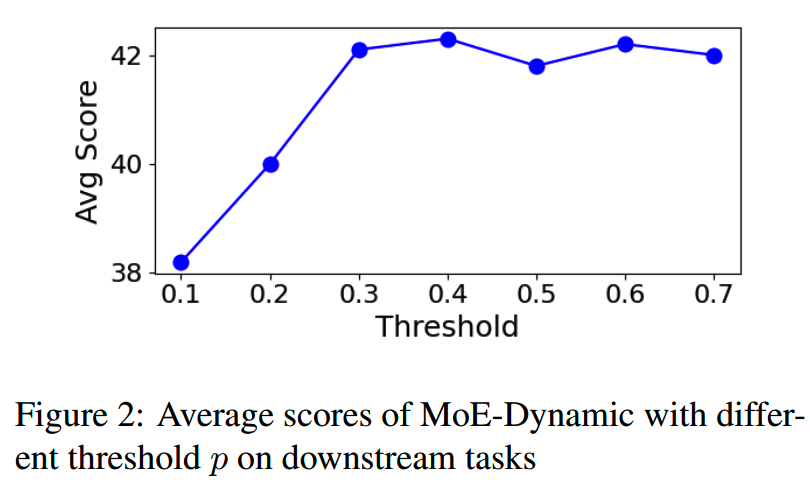
当p值特别低比如0.1或者0.2时,效果比较差,而p≥0.3之后基本就效果保持在比较好的水平了。
激活专家收敛
top-p MoE在训练一开始激活的专家数会比较多,而随着训练进行,激活专家数逐渐下降:
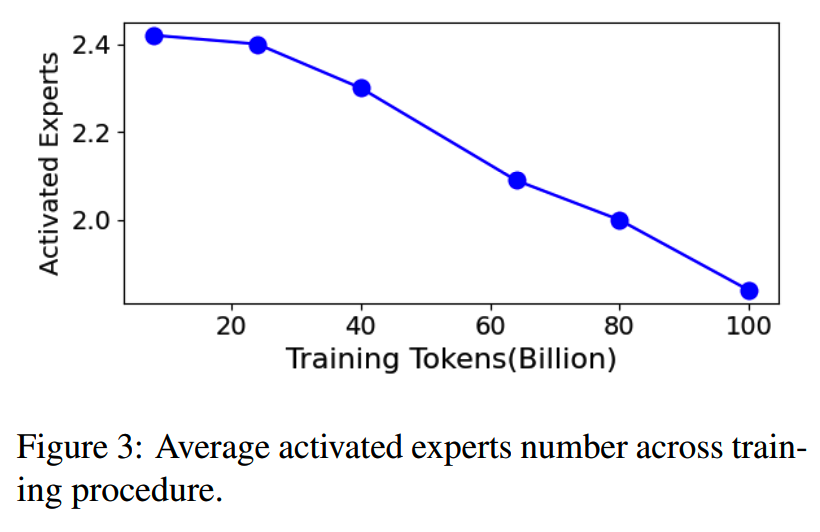
可以看到在60B以后就逐渐低于2了,并且从图上看还有下降趋势。这里实验只做了100B,如果训了1T或者10T,应该会有更大的收益。
top-p MoE适合更难的任务
BBH(BIG-Bench Hard),包括了23个比较有挑战性的BIG-Bench任务。
从下图可以看到,相比其他任务,模型在BBH任务会激活更多的专家
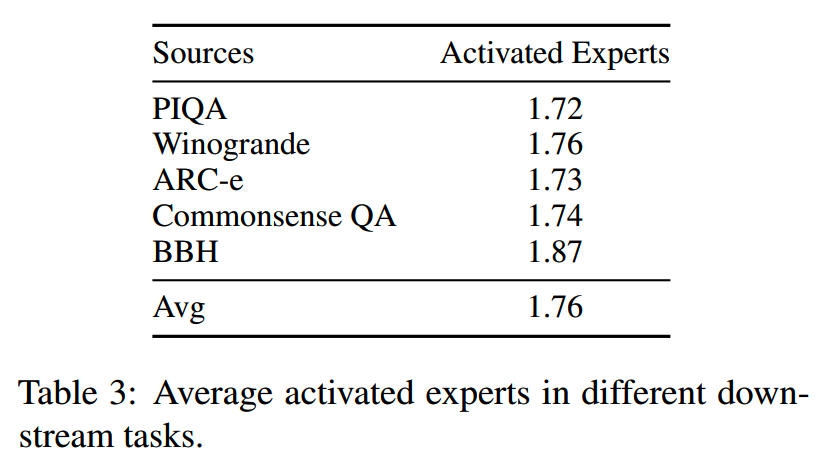
并且相对于其他下游任务,top-p MoE在BBH上的提升也是最多的。
这说明top-p MoE允许模型激活更多的专家,以获得足够的能力和信息,从而能在更难的任务上进一步提升效果。
底层需要激活更多专家
top-p MoE以更少的激活参数量在下游任务取得更好的效果,这归功于专家在不同层间的合理分配。
下图给出模型不同MoE层的平均激活专家数量
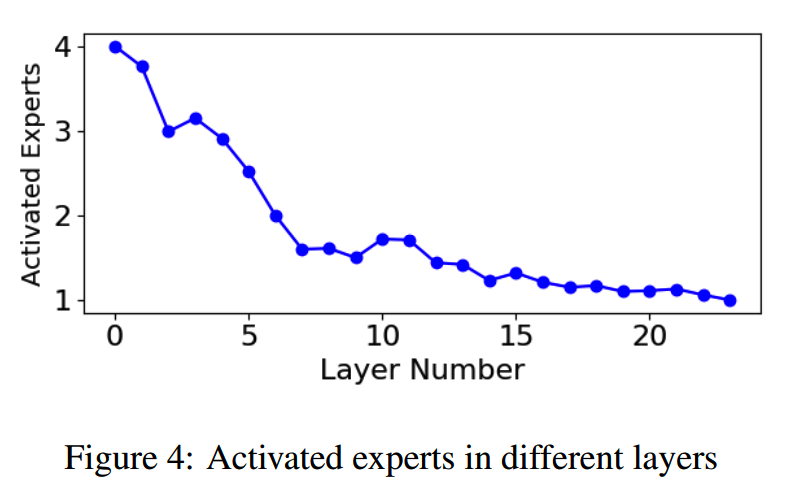
这样的现象和overthinking有些相似。
按《Shallow-deep networks: Understanding and mitigating network overthinking》说法,overthinking指相对于最终层的复杂表示,更早期层中输入样本的更简单表示就足以做出正确的预测。
随着层数增多,激活的专家数量逐渐下降。模型能够把更多的计算budget用在收益更大的浅层表征,提升最终效果。
小结
- 解除MoE模型的专家激活数限制,可以让模型自由选择需要的专家,以应对更难的任务,应该是个不错的思路。
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

【往期文章】
MoE模型的前世今生
DeepSeek-V2和MLA
昆仑万维-SkyworkMoE
成本10w刀的JetMoE
从loss视角理解大模型涌现能力
LLM长上下文的问题
解锁大模型长上下文能力
大模型推理窗口-从有限到无限大
理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
大模型推理加速-MEDUSA
LLM的重复生成和ICL
大模型偏好对齐-DPO
大模型偏好对齐-ODPO
大模型偏好对齐-simPO
大模型偏好对齐-IPO
Yi技术报告-划重点看细节
MiniCPM
GLM4报告的一些技术点
Gemma2
苹果的OpenELM
从Yuan2.0到Yuan2.0-M32
bilibili的index-1.9B
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding
window attention
理解LLM位置编码:RoPE
RoPE的远距离衰减
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)
大模型算法题(7)
Reference
【1】Harder Tasks Need More Experts: Dynamic Routing in MoE Models https://arxiv.org/abs/2403.07652