RoPE的远距离衰减

发表于 2024-06-25 更新于 2024-06-26 分类于 CS ， NLP ， LLM 本文字数： 4.2k 阅读时长 ≈ 8 分钟

【本文已在同名微信公众号 / 知乎 / 个人博客linsight.cn 上线】

有朋友问到了关于RoPE远距离衰减的问题，这里给出几个示例，提供一个直观理解的视角。

公式

回顾一下RoPE的实现。RoPE通过在q和k上分别乘一个旋转矩阵，实现了相对距离编码的功能。

对于position为m的q或者k，旋转矩阵如下

\[ \boldsymbol{R}_{\Theta,m}^d=\begin{pmatrix}\cos m\theta_0&-\sin m\theta_0&0&0&\cdots&0&0\\\sin m\theta_0&\cos m\theta_0&0&0&\cdots&0&0\\0&0&\cos m\theta_1&-\sin m\theta_1&\cdots&0&0\\0&0&\sin m\theta_1&\cos m\theta_1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\\0&0&0&0&\cdots&\sin m\theta_{d/2-1}&\cos n\theta_{d/2-1}\end{pmatrix} \]

实际实现时，高效率的实现如下

\[ \boldsymbol{R}_{ m}\boldsymbol{q}=\begin{pmatrix}q_0\\q_1\\q_2\\q_3\\q_4\\\vdots\\q_{d-2}\\q_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{pmatrix} +\begin{pmatrix}-q_1\\q_0\\-q_3\\\vdots\\-q_{d-1}\\q_{d-2}\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0\\\sin m\theta_0\\\sin m\theta_1\\\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{pmatrix} \]

也可以让第二项保持输入向量的元素位置，变成

\[ \boldsymbol{R}_{ m}\boldsymbol{q}=\begin{pmatrix}q_0\\q_1\\q_2\\q_3\\q_4\\\vdots\\q_{d-2}\\q_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{pmatrix} +\begin{pmatrix}q_0\\q_1\\q_2\\q_3\\q_4\\\vdots\\q_{d-2}\\q_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0\\-\sin m\theta_0\\\sin m\theta_1\\-\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\-\sin m\theta_{d/2-1}\end{pmatrix} \]

huggingface的实现中预先把各个位置的cos额sin向量都计算好了，可以重复利用，这样看后面这样实现的效率会更高一点。

远距离衰减

远距离衰减指的是随着q和k的相对距离的增大，加入位置编码之后的内积应该随着距离增大而减小，这样相当于离得远的token分配到的attention会比较小，而离得近的token会得到更多的注意力。

这样的特性确实直觉上比较符合人类的注意力机制。

把各个参数（base、window size、head size）下的内积值画出来看看是怎么衰减的。实现参考下面的代码。这里偷懒没有实现得很高效，勉强能用就行。


import random
import numpy as np
import matplotlib.pyplot as plt

def apply_rope(input_vec, position, base=10000):
    # 获取维度
    d = input_vec.shape[0]
    
    # 获取theta
    i = np.arange(1, d // 2 + 1)
    theta = base ** (-2 * (i - 1) / d)
    theta = np.repeat(theta, 2)
    
    # 计算旋转后的向量
    reranged_vec = np.empty_like(input_vec)
    reranged_vec[0::2] = -input_vec[1::2]
    reranged_vec[1::2] = input_vec[:-1:2]
    output_vec = input_vec * np.cos(position * theta) + reranged_vec * np.sin(position * theta)
    
    return output_vec


def plot(x, y, name=''):
    plt.plot(x, y, label=name)
    plt.legend()
    # 显示图表
    plt.show()
    
base = 10000
window_size = 4096
d = 512

q = np.ones(d)
k = np.ones(d)

rotated_q = apply_rope(input_vec=q, position=0, base=base)

inner_products = []
for i in range(window_size):
    rotated_k = apply_rope(input_vec=k, position=i, base=base)
    product = np.dot(rotated_q, rotated_k)
    inner_products.append(product)
    
plot(x=range(window_size), y=inner_products, name=f'base={base},window size={window_size},d={d}')

（1）q = k = 1

假设q和k都是1向量，如果q在位置0，画出k在0~4096位置下和q在位置编码后的内积如下。

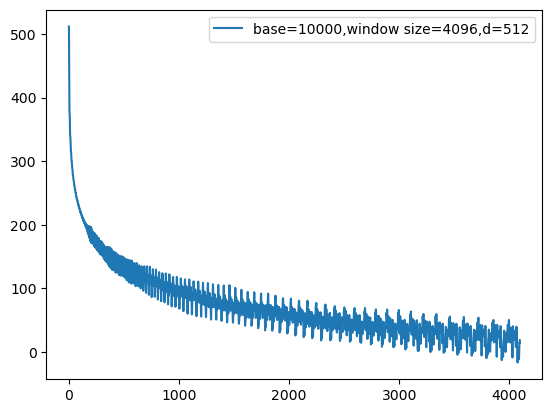
这里使用了base=10000，d=512。

可以看到整体趋势是震荡下降的

不过如果把窗口从4096增大到65536，图像会变成这样

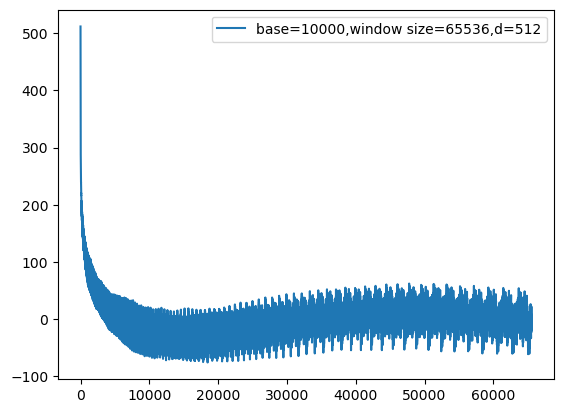
可以看到图像不再是单纯的衰减，在距离超过大约15000的时候，出现了上升。

实际上这个包含多个周期函数的内积也具有一定的周期性，并不是在整个域上保持衰减的特性。只要相对距离够大，超过这个周期的1/4，内积就会再次上升。

而这个内积的周期受base调控，base越大，周期越长，因此现在的长窗口模型起步就是base=5M或者10M。

我们把base改成5M，图像如下

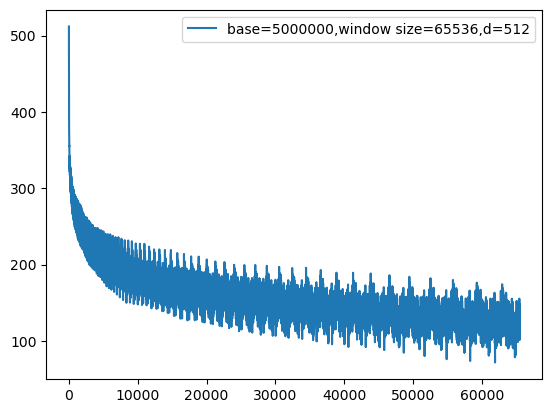
又呈现了震荡衰减的趋势。

前面画的是q在位置0，k在0~4096/65536的情况，那么把q放在中间看看内积结果怎么样。

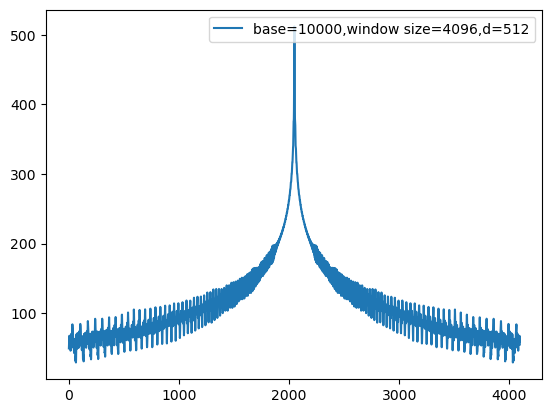
可以看到在q两边的内积是对称的，同样的远距离衰减属性。

（2）q、k随机

前面是把q和k固定为1向量，现在试着把q和k初始化为随机向量，图像如下

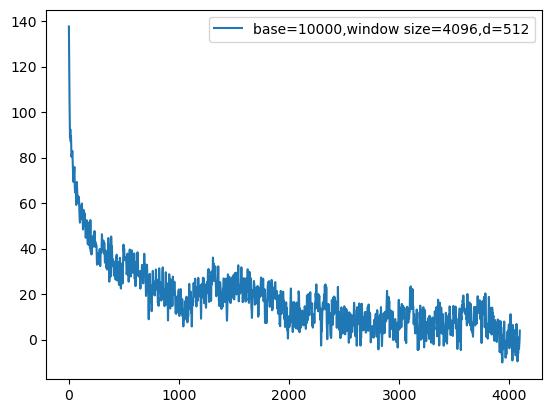
相比1向量出现了更多的震荡，但是大体上还是能保持一定的远距离衰减特性。

小结

RoPE的远距离衰减是震荡的，并且整个内积本身也具有一定的周期性，只有把base设得足够大，才能让内积结果在模型窗口大小内保持远距离衰减的特性。
在q和k的相对距离小的时候，内积差距较大，也就是衰减较快；到了远距离之后，衰减变慢，也就是从内积角度来看，分辨率会变小。

读到这了，来一发点赞收藏关注吧~

博客：http://www.linsight.cn/
知乎：Linsight
微信公众号：Linsight

【往期文章】

MoE模型的前世今生
 昆仑万维-SkyworkMoE
从loss视角理解大模型涌现能力
 LLM长上下文的问题
 解锁大模型长上下文能力
 大模型推理窗口-从有限到无限大
 理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
 大模型推理加速-MEDUSA
LLM的重复生成和ICL
大模型偏好对齐-DPO
大模型偏好对齐-ODPO
大模型偏好对齐-simPO
大模型偏好对齐-IPO
Yi技术报告-划重点看细节
 MiniCPM
transformer中normalization的二三事
 从代码实现看normalization-到底做了什么
 稀疏注意力计算:sliding window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)
大模型算法题(7)

Reference

【1】Transformer升级之路：2、博采众长的旋转式位置编码，https://spaces.ac.cn/archives/8265
【2】RoFormer: Enhanced Transformer with Rotary Position Embedding https://arxiv.org/abs/2104.09864
【3】理解LLM位置编码:RoPE http://www.linsight.cn/c4da56c0.html