大模型推理加速-MEDUSA

发表于 2024-06-11 更新于 2024-06-15 分类于 CS ， NLP ， LLM 本文字数： 6.7k 阅读时长 ≈ 12 分钟

【本文已在同名微信公众号 / 知乎 / 个人博客linsight.cn 上线】

之前对speculative decoding的做法做了介绍：大模型推理加速-投机解码。

本篇介绍一下另外一个热门的解码加速算法，MEDUSA。MEDUSA在不同的训练方法下能提供×2.2~×2.8的解码加速效果。

背景

自回归大模型推理下一个token的时候，需要依赖前面的结果。而在实际使用GPU进行计算时，需要将相关矩阵移至片上内存进行运算，而一般来说片上内存带宽比计算性能要低两个数量级，这就使得大模型推理是memory-bandwidth-bound的。

要解决这个问题，一个思路是increasing the arithmetic intensity，即提高“浮点数计算量/数据传输量”这个比值，让数据传输不要成为瓶颈。另一个思路是reducing the number of decoding steps。投机解码就属于后者。

不过投机解码有几个问题：
- 一个好的draft model不容易获取：draft模型和原模型存在distribution shift
- 推理时有多个模型参与，在分布式系统上的部署难度增大

而MEDUSA相比投机解码，不需要新增一个模型，而是基于原模型进行并行推理，这样训练难度更低，部署也更容易。

MEDUSA

MEDUSA的大致思路是和投机解码类似：
- 首先生成各个位置的候选token；MEDUSA通过接在原模型的多个解码头来获取多个位置的候选token
- 把各个位置的候选token进行处理，选出一些候选序列，进行验证；MEDUSA通过tree attention来处理
- 最后通过typical acceptance选择最终输出的结果

MEDUSA的pipeline如下图所示

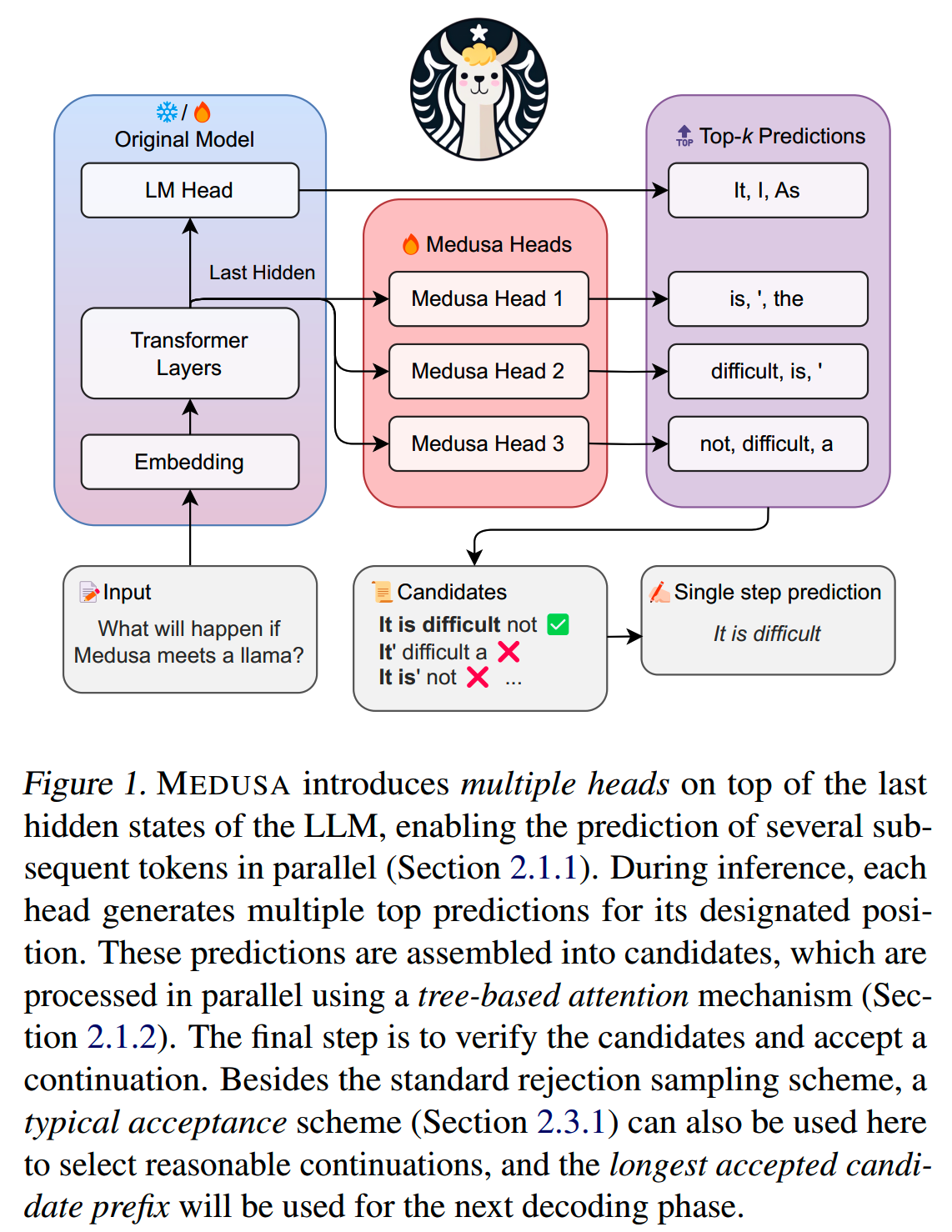
MEDUSA的这些分类头需要经过训练才能有比较好的预测效果。针对不同的条件，可以选择不同的训练方式：
- MEDUSA-1：冻结原模型的backbone（包括原模型的解码头），只训练增加的解码头。这种方案适用于计算资源比较少，或者不想影响原模型的效果的情况。还可以使用QLoRA对解码头进行训练，进一步节省memory和计算资源。
- MEDUSA-2：原模型和MEDUSA的解码头一起训练。MEDUSA-1这样的训练方法虽然可以节省资源，但是并不能最大程度发挥多个解码头的加速效果，而MEDUSA-2则可以进一步发挥MEDUSA解码头的提速能力。MEDUSA-2适用于计算资源充足，或者从Base模型进行SFT的场景。

另外，如果原模型的SFT数据集是available的，那可以直接进行训练。如果不能获得原模型的SFT数据，或者原模型是经过RLHF训练的，则可以通过self-distillation来获取MEDUSA head的训练数据。

模型设计：MEDUSA HEADS

先来看下第一步，MEDUSA的多个解码头是怎么给出各个位置的候选token的。

假设原始模型最后一层的hidden state在时间 $t$ 的输出是 $h_{t}$，我们给模型额外加上 $K$ 个解码头。那么第 $k$ 个头就可以用来预测位置 $t+k+1$ 的输出token（这里 $k$ 的取值为 $1$ ~ $K$）。这里注意原模型自己还有一个解码头，它依然用来预测位置 $t+1$ 的输出，相当于 $k=0$。

把第 $k$ 个解码头在vocabulary上的输出分布写作 $p_t^{(k)}$，其计算方式如下

\[\begin{aligned}p_t^{(k)}=\text{softmax}\left(W_2^{(k)}\cdot\left(\text{SiLU}(W_1^{(k)}\cdot h_t)+h_t\right)\right),\\\mathrm{where~}W_2^{(k)}\in\mathbb{R}^{d\times V},W_1^{(k)}\in\mathbb{R}^{d\times d}.\end{aligned}\]

$d$ 是hidden state的输出维度，$V$ 是词表大小。每个解码头其实就是一个FFN网络，实践上发现这样简单的设计已经有足够好的效果。

在初始化各个解码头的参数时，把 $W_2^{(k)}$ 初始化成和原模型的解码头一样，而把 $W_1^{(k)}$ 设置成0。这样能使得在一开始训练的时候，增加的这些解码头就有一定的预测能力。

这 $K$ 个新增的解码头直接在原模型的基础上进行训练，因此相比投机解码的draft model，MEDUSA的训练方式缓解了distribution shift的问题。

候选校验：TREE ATTENTION

Cartesian product

增加额外的解码头之后，模型每次前向推理都会给出 $K+1$ 个位置的候选token。

投机解码里是直接选出draft model最有信心的一个候选序列给原模型进行验证。

显然，如果增加候选序列的数量，那么最终接受token的命中率就会提升，acceleration rate（即每个decoding step能获得的token数，不是实际解码时间）也就更高，但是验证更多候选序列也会带来额外的计算消耗。为了获得一个效果和性能比较好的平衡，MEDUSA使用tree attention来同时对多个候选序列进行处理。

假设第 $k$ 个解码头给出的候选token数量是 $s_k$ 个，那么可以通过Cartesian product来获取多个解码头组成的所有可能的候选序列，然后用tree attention对所有候选序列进行验证。

对于两个解码头的情况，tree attention验证的示意图如下

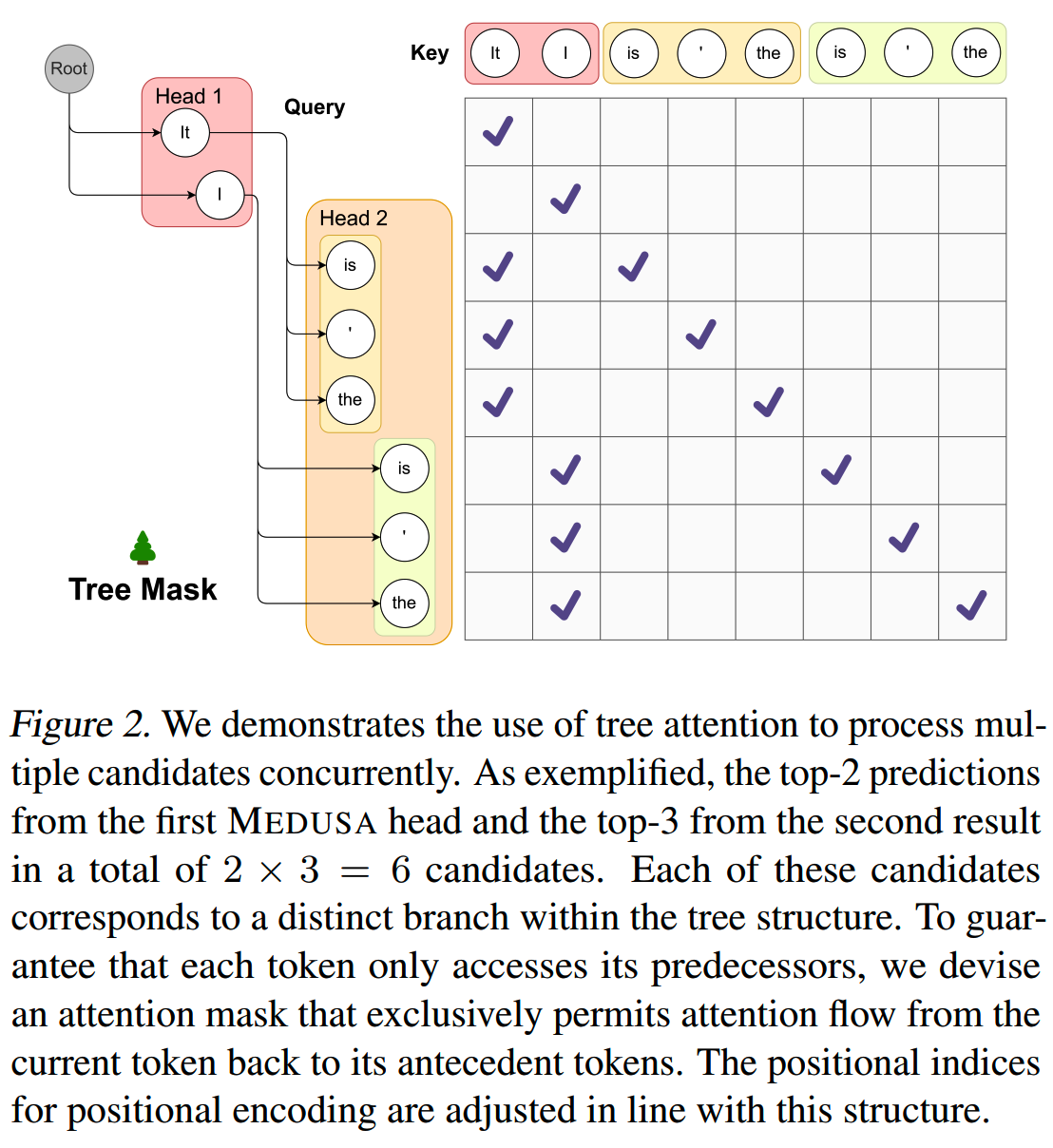
通过使用这样的mask，我们可以在不扩大batch size的情况下同时处理多个候选序列。（注意，这里要对各个候选token的位置编码进行处理。）

更高效的tree attention构建

上面这个例子使用了Cartesian product对两个解码头的结果进行处理，获得所有候选序列。

但是如果解码头数量数量比较多，每个头给出的候选token也比较多，那么实际要验证的序列数量会极大地增长。

直觉上，这些解码头应该有不同的准确率，因此可以利用这一点来构建tree attention，而不需要使用所有可能的排列组合。

具体来说，可以使用一个calibration dataset（比如Alpaca-eval dataset）来获取不同解码头给出的各个token的准确率：把第 $k$ 个解码头给出的第 $i$ 个token的准确率记为 $a_k^{(i)}$。

假设各个token的准确率之间是独立的，那么一个由 $[i_1,i_2,\cdots,i_k]$ 构成的候选序列的准确率可以写作 $\prod_{j=1}^ka_j^{(i_j)}$。

每个候选序列可以表示所构建的tree上的一条路径上所有的node（而不只是leaf node，因为tree attention验证的时候会把路径上所有token都进行验证）。用 $I$ 表示候选序列的集合，那么集合里的候选序列的expectation of acceptance length就表示为

\[\sum_{[i_1,i_2,\cdots,i_k]\in I}\prod_{j=1}^ka_j^{(i_j)}\]

在构建tree的时候，优先加入当前有最大准确率的候选序列，直到tree的节点数量达到上限，这样能最大化expectation of acceptance length，也就能最大化acceleration rate。

下图是一个按这种方法构建的tree的例子。可以看到这棵树向左偏，这是因为这个方法倾向于使用更高准确率的token。

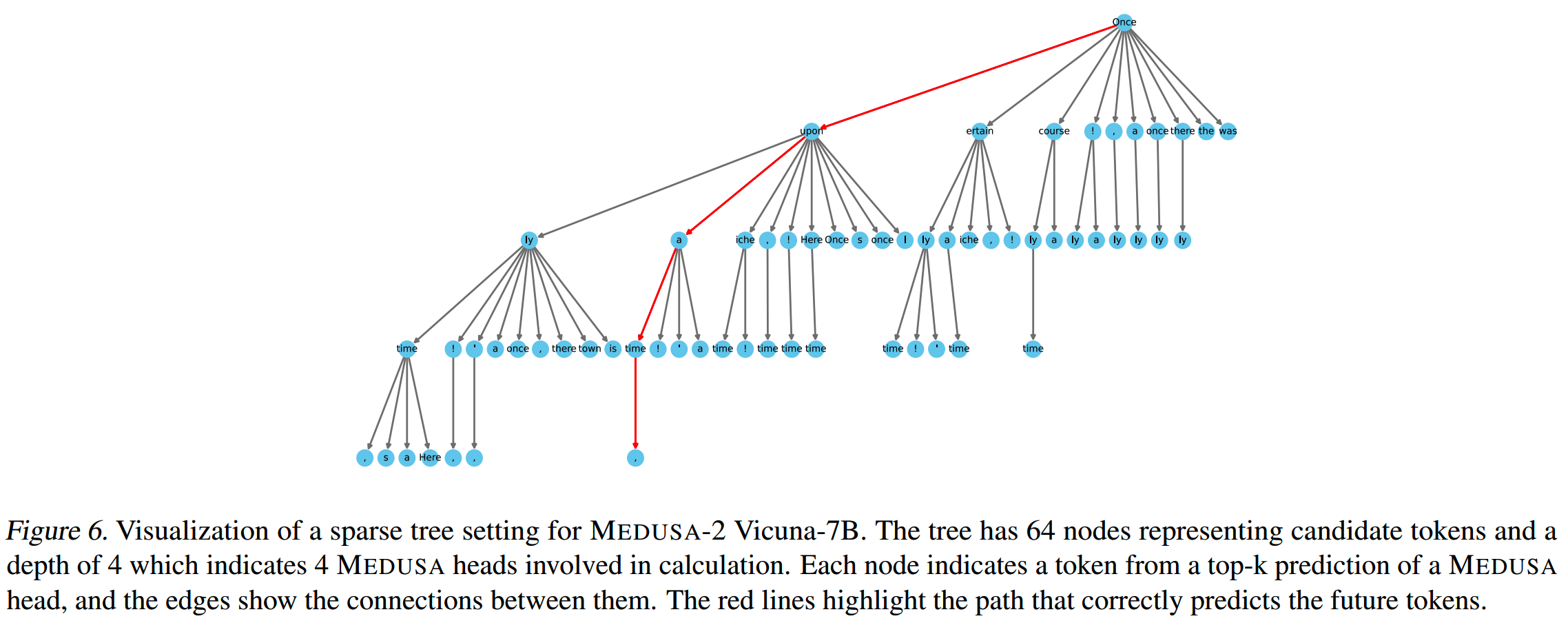
训练策略

MEDUSA的解码头需要进行训练。训练策略根据是否有“与模型输出分布对齐的训练数据”而有所不同。

有训练数据

MEDUSA-1冻结了原模型的参数，而只对新增的解码头进行训练。

第 $k$ 个解码头的训练loss可以写作

\[\mathcal{L}_k=-\log p_t^{(k)}(y_{t+k+1})\]

总的训练loss为

\[\mathcal{L}_{\text{MEDUSA-l}}=\sum_{k=1}^K-\lambda_k\log p_t^{(k)}(y_{t+k+1})\]

这里的 $\lambda_{k}$ 是每个解码头的缩放系数，是一系列超参。因为 $k$ 越大，对应解码头的预测难度越大，loss也就越大，为了防止靠后的解码头过分主导训练，因此使用一个缩放系数进行调整。

实际使用中，$\lambda_{k}=0.8^{k}$。

训练时，由于冻结了原模型，因此可以对原模型的参数进行量化而不会对训练效果有明显影响，比如使用QLoRA。

MEDUSA-1冻结了原模型，比较适用于计算资源有限，或者希望保持原模型能力的场景。如果要进一步发挥MEDUSA多个解码头的加速效果，那就需要使用MEDUSA-2。

MEDUSA-2把原模型和多个解码头一起训练，因此各个解码头的准确率能达到更高的水平，acceleration rate也更高。但是为了保持原模型的输出质量，需要使用以下三个措施。

（1）Combined loss

首先是加入原模型next-token prediction的loss，即把原模型解码头的loss也加上，如下式

\[\mathcal{L}_{\text{MEDUSA-}2}=\mathcal{L}_{\text{LM}}+\lambda_0\mathcal{L}_{\text{MEDUSA-}1}\]

\[\mathcal{L}_{\text{LM}}=-\log p_t^{(0)}(y_{t+1})\]

实际使用中，直接训练时 $\lambda_0=0.2$，使用self-distillation时$\lambda_0=0.01$。

（2）Differential learning rates

原模型已经是训练好了的，因此和新加入的解码头使用相同的学习率并不合适，因此可以让新的解码头使用更大的学习率，而原模型参数使用相对小的学习率。实践中把学习率差距设为4倍，比如分别使用2e-3和5e-4。

（3）Heads warmup

新加入的解码头在一开始训练会有比较大的loss，从而导致更大的梯度，有可能损害原模型的能力。

针对这个问题，可以使用two-stage training的方式，先在MEDUSA-1的策略下训练解码头，然后再进行MEDUSA-2的训练。这其实相当于把 $\lambda_0$ 在训练过程中逐渐增大。two-stage training和逐渐增大 $\lambda_0$ 的方法在实践中都是可行的。

SELF-DISTILLATION

前面讲的这些训练方式都有一个前提，那就是有与模型输出分布对齐的训练数据可供使用。但是实际上这个前提并不总是成立。比如大部分开源模型并没有发布相应的SFT数据，或者模型使用了RLHF等对齐方式，而不是直接SFT。

解决方法是使用self-distillation：通过原模型为MEDUSA解码头生成训练数据。

首先选择一个和target model的domain相近的数据集，然后把prompt输入给原模型，获得原模型的输出。对于对话模型，需要生成多轮对话，可以使用self-talk。

对于MEDUSA-1，这样生成的数据集已经够用，但是对于MEDUSA-2，这样的训练会降低生成质量。

实际上，即使不进行MEDUSA解码头的训练，只用生成的数据训练原模型，原模型的效果也会变差。因此MEDUSA-2训练的时候，原模型的训练不应该直接使用ground truth进行训练，而是进行蒸馏，按下式计算损失

\[\mathcal{L}_{\text{LM-distill}}=KL(p_{\text{original},t}^{(0)}||p_t^{(0)})\]

接受策略：TYPICAL ACCEPTANCE

投机解码随着temperature的提升，命中率会降低。因为temperature提升，draft model所选择的候选token的多样性就增大，也就降低了命中原模型token，从而被接受的概率。

但是这种特性并不合理。通常更高的temperature参数一般对应更强的creativity特性，因此合理的情况应该是随着温度提高，候选序列有更大的概率被接受。这和投机解码的情况是相反的。

另外，MEDUSA认为候选序列的分布没有必要完全match原模型的分布。我们要做的应该是选出typical的候选，也就是只要候选序列不是极不可能的结果，就可以被接受。

给定context $x_1,x_2,\cdots,x_n$，候选序列 $(x_{n+1},x_{n+2},\cdots,x_{n+K+1})$，我们按以下这个条件来接受候选token

\[\begin{aligned}p_{\text{original}}(x_{n+k}|x_1,x_2,\cdots,x_{n+k-1})&>\\\min\left(\epsilon,\delta\exp\left(-H(p_{\text{original}}(\cdot|x_1,x_2,\cdots,x_{n+k-1})))\right)\right),\end{aligned}\]

其中 $H(\cdot)$ 表示entropy function，$\epsilon,\delta$ 分别是hard threshold和entropy-dependent threshold。

两个threshold的解释：（1）$\epsilon$ 保证所选的token的概率不能低于特定值，保证不选出可能性很低的结果（2）当一个位置的多个候选token的entropy较高时，表示多个候选都是reasonable的，那么 $\delta$ 和exp(entropy)的乘积会更小，各个token都有更大的机会被接受。

当temperatrue为0的时候，相当于贪心解码，这个时候只有概率最大那个token有非0概率。随着温度提升，其他token的概率也提升，因此它们也有一定的机会被接受。随着温度提升，这些token被接受的概率会增大。

最后选择被接受的解码长度最长的候选序列作为最终结果。

消融实验

CONFIGURATION OF TREE ATTENTION

对比通过准确率构建tree attention的方式，和随机构建tree attention的方式，结果如下

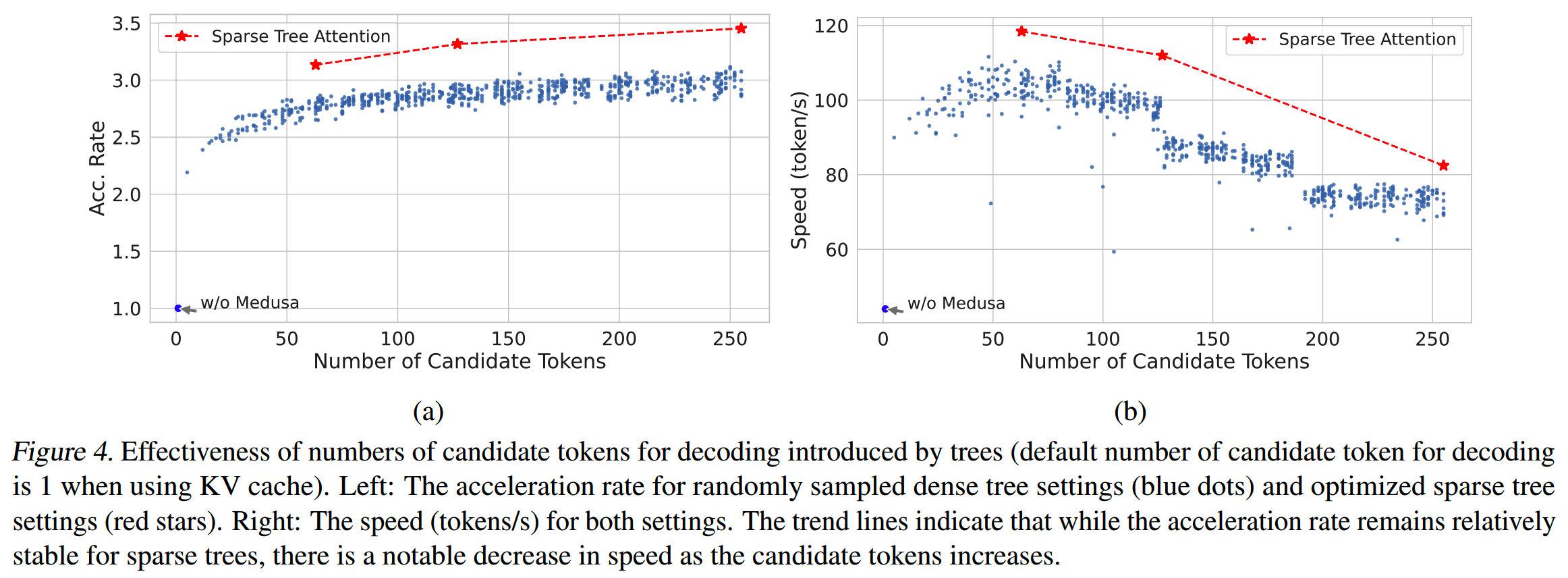
基于准确率构建的tree attention有更高的acceleration rate。

但随着候选token数量的增加，两种方式的实际速度反而有所下降，因为更多的候选token引入了额外的计算成本。

THRESHOLDS OF TYPICAL ACCEPTANCE

随着 $$ 增加，输出质量得到提升，但代价是acceleration rate降低，如下图

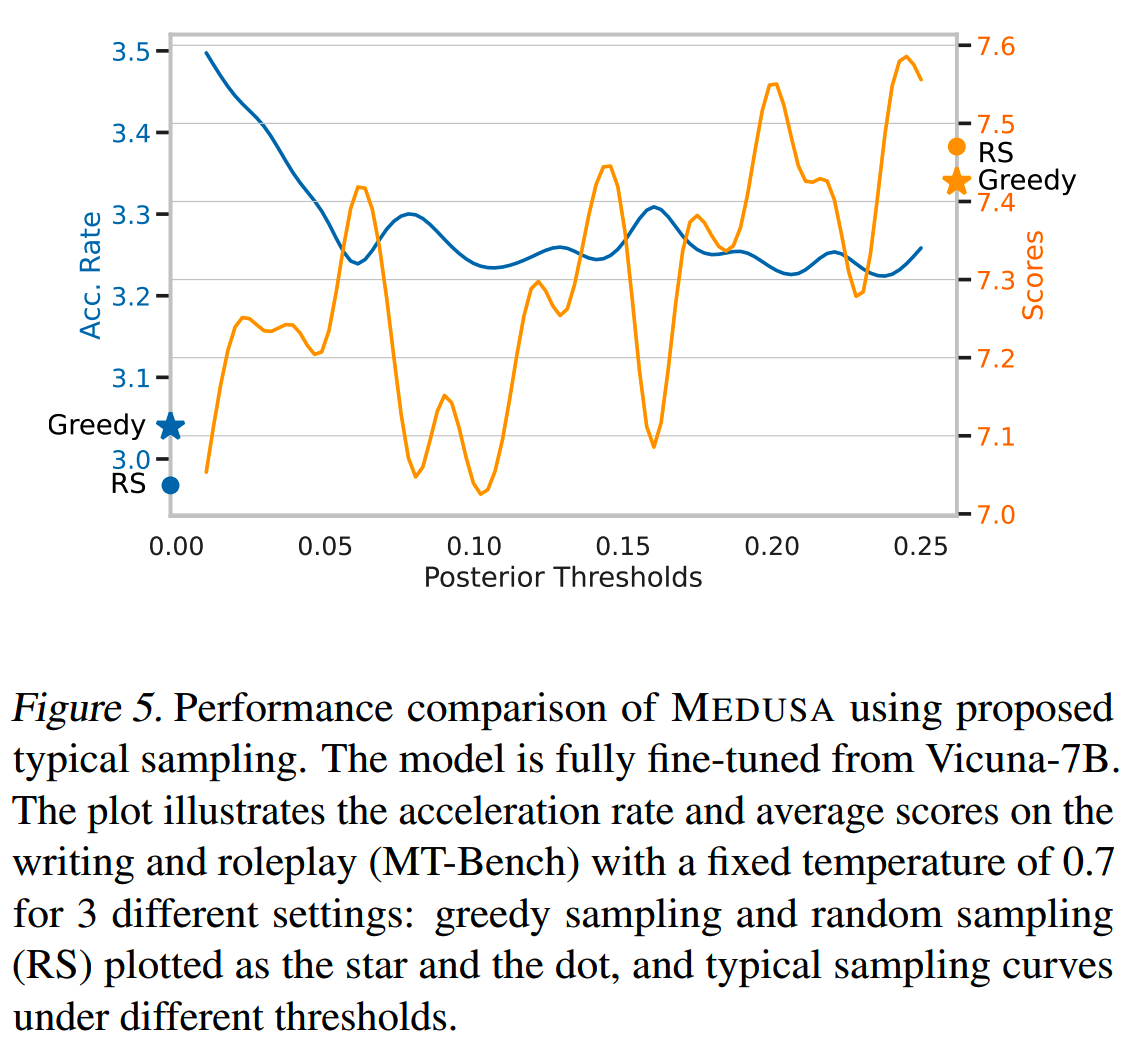
各环节对速度的影响

各个技术优化点对速度的影响如下表

小结

MEDUSA引入了tree attention、typical acceptance的做法，在加速比上相比投机解码有进一步提升。

但是MEDUSA不保证解码结果和原模型一致，因此应该更适用于对模型生成质量的没有那么严格要求的场景。

读到这了，来一发点赞收藏关注吧~

博客：http://www.linsight.cn/
知乎：Linsight
微信公众号：Linsight

【往期文章】

MoE模型的前世今生
 昆仑万维-SkyworkMoE
LLM长上下文的问题
 解锁大模型长上下文能力
 大模型推理窗口-从有限到无限大
 理解Attention:从起源到MHA,MQA和GQA
大模型推理加速-投机解码
 大模型偏好对齐-DPO
大模型偏好对齐-ODPO
大模型偏好对齐-simPO
大模型偏好对齐-IPO
Yi技术报告-划重点看细节
 transformer中normalization的二三事
 从代码实现看normalization-到底做了什么
 稀疏注意力计算:sliding window attention
理解LLM位置编码:RoPE
大模型算法题(1)
大模型算法题(2)
大模型算法题(3)
大模型算法题(4)
大模型算法题(5)
大模型算法题(6)

Reference

【1】MEDUSA: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads https://arxiv.org/abs/2401.10774