MoE路由--expert choice routing
【本文已在同名 微信公众号 / 知乎 / 个人博客linsight.cn 上线】
MoE模型两大主要组件就是gating network和expert network。
gating决定了选择专家的方式、各个专家权重和专家数量。
目前大部分主流的MoE模型都是token choice routing(或者直接叫top-k routing),即根据输入token和所有专家的匹配得分,选择匹配度最高的k个专家进行处理,以加权和作为对应token的输出。
那么也有反过来,根据专家和所有token的匹配度,选择每个专家处理的token的做法,就是expert choice routing(EC)。
两种routing的示意图如下
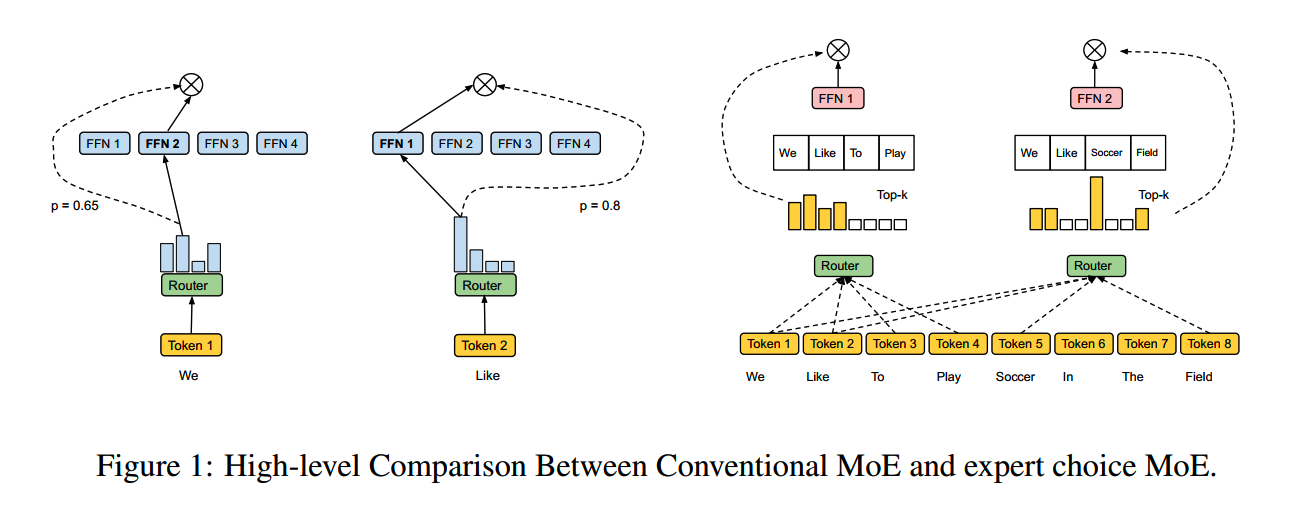
token choice routing有点像大学课堂,老师就是专家,每个学生就是token,每个学生选择最适合自己的老师。而expert choice有点像中小学课堂,由每个老师选择上课的班级。
token choice routing的弊端
虽然目前主流的MoE都是使用token choice routing,但是它也还存在一些问题。
1、Load Imbalance
各个专家间的负载均衡问题从2017年的《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》里就有专门拉出来讨论。
负载不平衡主要是因为token choice是独立为每个token选择k个专家,而没有考虑所选择的这k个专家是否被其他token选择。
如果有几个专家训练得特别好,那么它们就会很容易被各个输入token选中,从而又使得这几个专家训练得更充分,和其他没有训练足够的专家的得分差距继续拉大,出现马太效应,造成恶性训练。
如果负载出现不平衡的情况,会削弱MoE模型的推理效率,因为每层都要等所有专家处理完,而这又取决于负载最大的专家的耗时。
后续的Gshard、Switch Transformer和ST-MoE,到现在的Qwen2-MoE和DeepSeek-MoE等,基本固定了使用多个level的负载均衡损失来缓解这个问题。
2、Under Specialization
如很多MoE模型提到的,加入负载均衡损失并不能完全解决负载问题,而如果过于强调负载均衡,使用比较大的权重系数,模型的效果也会有一定的损失。因为这样gating可能会被迫把一些token分配给没有充分训练的专家。从效果上考虑,增大负载均衡损失的权重显然不是最好的方案。
3、Same Compute for Every Token
token choice routing有一个隐含的假设是每个输入token都需要由相同数量的expert来处理,但经验来说这并不是最合理的:一般来说,更难的token可能需要更多专家,而相对简单的token可能只需要一个专家就能解决,而不需要k个专家。
直接对所有token使用固定k个专家,可能限制了模型计算资源的更合理分配。
expert choice routing
方法
expert choice routing的思路是让每个expert选择当前所有输入token(比如一个batch)中和自身匹配度最高的k个token来处理。
假设共有n个输入token,专家的数量为e,那么k的值为:
\[k=\frac{n\times c}e\]
c是超参capacity factor,代表每个token平均会有多少个expert来处理,这和token choice routing一样。
对于输入 \(X\in\mathbb{R}^{n\times d}\) (d是hidden size),expert choice routing用到3个矩阵I、G、P来操作。
\[S=\mathrm{Softmax}(X\cdot W_g),\quad S\in\mathbb{R}^{n\times e}\\G,I=\mathrm{TopK}(S^\top,k),P=\mathrm{Onehot}(I)\]
\(W_g\in\mathbb{R}^{d\times e}\) 表示expert embedding。S表示所有专家和所有输入token之间的匹配程度。
I是index matrix,\(I[i,j]\) 表示第i个expert选择的第j个token(按得分排序)。
\(G\in\mathbb{R}^{e\times k}\) 是gating matrix,表示各个expert所选token的权重。
P是permutation matrix,是I的one-hot版本,把token分配给各个专家:
\[X_{in}=P\cdot X\]
\(X_{\mathrm{in}}\in\mathbb{R}^{e\times k\times d}\) 是发个各个专家的输入。\(X_\text{in}[i]\in\mathbb{R}^{k\times d}\) 表示给第i个专家的输入。
每个专家的输出 \({X}_e[i]\) 如下计算:
\[X_e[i]=\mathrm{GeLU}(X_{in}[i]\cdot W_1[i])\cdot W_2[i]^\top \]
最终MoE层的输出 \(X_{\mathrm{out}}\in\mathbb{R}^{n\times d}\) 可由P和G得到:
\[X_\mathrm{out}[l,d]=\sum_{i,j}P[i,j,l] G[i,j] X_e[i,j,d]\]
加上constraint
上面这样实施的expert choice routing存在一个问题,那就是可能大部分expert甚至所有expert都选中了同一个token,相当于这个token会被分配到所有token来处理。这样在通讯上可能会成为一个瓶颈。
针对这个问题,论文提出一个约束条件,给每个token所能分配到的最大expert数作了限制。
让 \(A\in\mathbb{R}^{e\times n}\) 表示 \(A[i,j]\) 表示第i个专家是否选择了第j个token。
通过以下约束优化问题,获得A,用 \(TopK(A,k)\) 代替I。
\[\max_A\left\langle S^\top,A\right\rangle+\lambda H(A)\]
\[\begin{aligned}H(A)=\sum_{ij}-A[i,j]\log A[i,j]\end{aligned}\]
\[\mathrm{s.t.}\quad\forall i:\sum_{j^{\prime}}A[i,j^{\prime}]=k; \forall j:\sum_{i^{\prime}}A[i^{\prime},j]\leq b; \forall i,j: 0\leq A[i,j]\leq1\]
b是每个token所能选择的最大专家数。H(A)是sum of element-wise entropy。加入H(A)项,文中给的理由是
Adding a small entropy term gives a near-integer solution while enabling a fast iterative solver we can run on TPUs.
实践中 λ = 0.001。
实验
实验中,每两层替换一层为MoE网络,所实验的各个模型参数如下

效果
1、Training Efficiency
从step数上看,相比GShard top-2 gating,EC-CF2在训练中的收敛速度 > 2x。
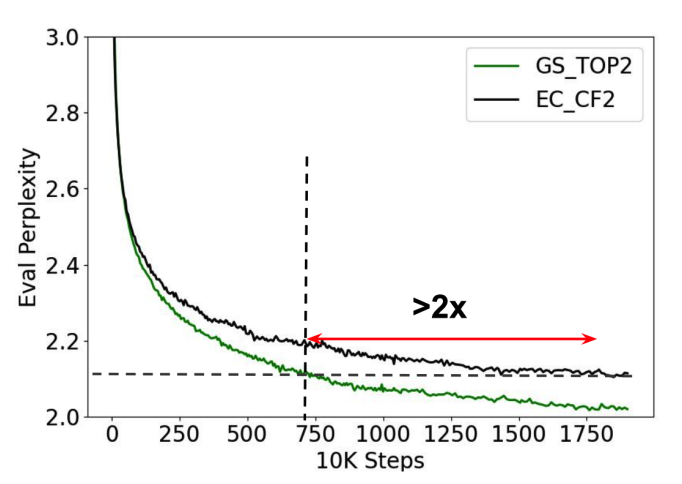
此外,EC-CF2每个step都比GShard top-2 gating快20%,也就是说从时间上看效率更高。
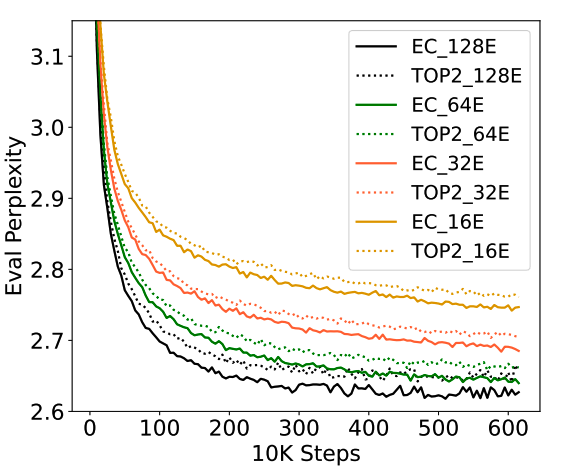
2、Scaling the Number of Experts
改变专家的数量,可以看到expert choice routing相比top-2 routing都有稳定的提升。
3、Capped Expert Choice
对每个token所能发送的最大专家数作了限制之后,效果对比如下:
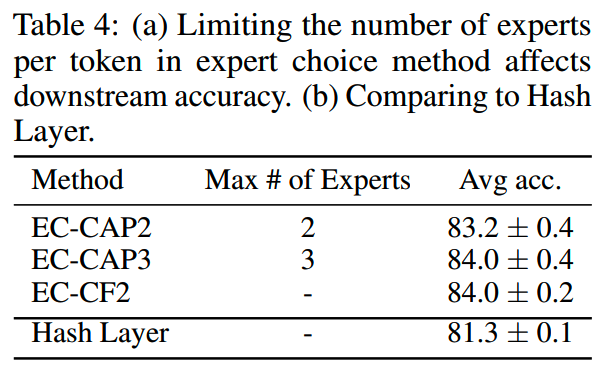
当限制专家数量为2时,效果有所下降,而限制专家数为3时,基本达到了和不加限制相同的效果。这说明允许每个token使用不同的专家数进行处理,确实是有效果的。
4、Variable Experts per Token
下图给出了token所用专家数量的分布。
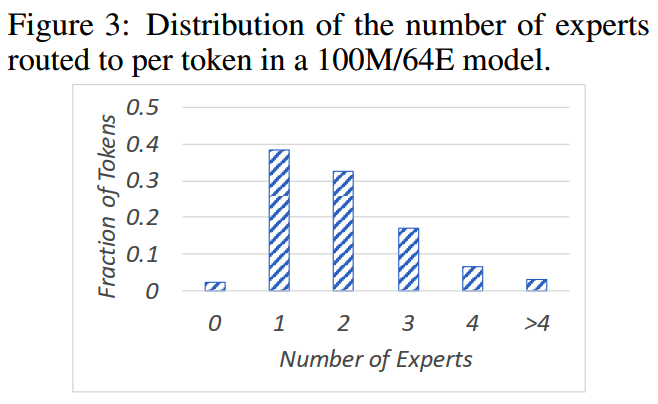
大多数token使用了一到两个专家,之后大约3%的token使用了四个以上的专家。
这里可以发现,还有少量的token没有专家处理,这是EC存在的一个问题。
消融实验
1、Capacity Factor
使用不同的CF,模型的效果对比如下。
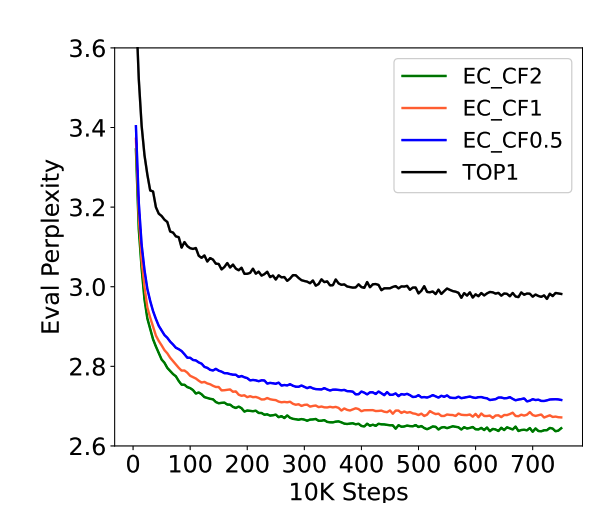
随着CF的增大,模型效果逐步提升。神奇的是,即使CF=0.5,即每个token平均只有0.5个专家处理,效果依然不错,甚至比switch transformer(top-1)高。
2、Comparison with Dense Models on Pre-training
EC在ppl和收敛时间上始终优于dense:
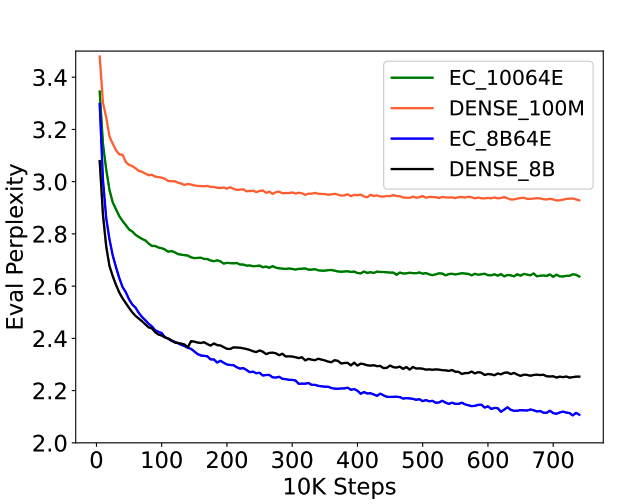
小结
- EC从思路上来看,相比token
choice确实有些优势,但是EC本身也存在一些问题,比如可能存在没有被任何专家选中的token。
- 另外在推理时如何结合cache等应该也是一个问题。
读到这了,来一发点赞收藏关注吧~
博客:http://www.linsight.cn/
知乎:Linsight
微信公众号:Linsight

【往期文章】
- MoE:
MoE模型的前世今生
DeepSeek-V2和MLA
昆仑万维-SkyworkMoE
成本10w刀的JetMoE
MoE的top-p
routing
对MoE模型的一些观察
从dense到MoE -- sparse
upcycling
- 预训练:
Qwen2技术报告
Yi技术报告-划重点看细节
MiniCPM
GLM4报告的一些技术点
Gemma2
苹果的OpenELM
从Yuan2.0到Yuan2.0-M32
bilibili的index-1.9B
从loss视角理解大模型涌现能力
- 长上下文:
LLM长上下文的问题
解锁大模型长上下文能力
大模型推理窗口-从有限到无限大
- 推理加速:
大模型推理加速-投机解码
大模型推理加速-MEDUSA
- 对齐:
大模型偏好对齐-DPO
大模型偏好对齐-ODPO
大模型偏好对齐-simPO
大模型偏好对齐-IPO
- Transformer:
理解Attention:从起源到MHA,MQA和GQA
LLM的重复生成和ICL
transformer中normalization的二三事
从代码实现看normalization-到底做了什么
稀疏注意力计算:sliding
window attention
理解LLM位置编码:RoPE
RoPE的远距离衰减
- 大模型算法题:
(1) (2) (3) (4) (5) (6) (7) (8)
Reference
【1】Mixture-of-Experts with Expert Choice Routing https://arxiv.org/abs/2202.09368